18. Работа и потенциальная энергия

1. С понятием энергии вы познакомились в курсе физики 7 класса. Вспомним его. Предположим, что некоторое тело, например тележка, съезжает с наклонной плоскости и передвигает лежащий у ее основания брусок. Говорят, что тележка совершает работу. Действительно, она действует на брусок с некоторой силой упругости и брусок при этом перемещается.

Другой пример. Водитель автомобиля, движущегося с некоторой скоростью, нажимает на тормоз, и автомобиль спустя какое?то время останавливается. В этом случае также автомобиль совершает работу против силы трения.

Говорят, что если тело может совершить работу, то оно обладает энергией.

Энергию обозначают буквой E. Единица энергии в СИ — джоуль (1 Дж).

2. Различают два вида механической энергии — потенциальная и кинетическая.

Потенциальной энергией называют энергию взаимодействия тел или частей тела, зависящую от их взаимного положения.

Потенциальной энергией обладают все взаимодействующие тела. Так, любое тело взаимодействует с Землей, следовательно, тело и Земля обладают потенциальной энергией. Частицы, из которых состоят тела, тоже взаимодействуют между собой, и они также обладают потенциальной энергией.

Поскольку потенциальная энергия — это энергия взаимодействия, то она относится не к одному телу, а к системе взаимодействующих тел. В том случае, когда мы говорим о потенциальной энергии тела, поднятого над Землей, систему составляют Земля и поднятое над ней тело.

3. Выясним, чему равна потенциальная энергия тела, поднятого над Землей. Для этого найдем связь между работой силы тяжести и изменением потенциальной энергии тела.

Пусть тело массой m падает с высоты h₁ до высоты h₂ (рис. 72). При этом перемещение тела равно h= h₁ – h₂. Работа силы тяжести на этом участке будет равна:

A = F_тяжh = mgh = mg(h₁ – h₂), или A = mgh₁ – mgh₂.

Величина mgh₁ = E_п1 характеризует начальное положение тела и представляет собой его потенциальную энергию в начальном положении, mgh₂ = E_п2 — потенциальная энергия тела в конечном положении. Формулу можно переписать следующим образом:

A = E_п1 – E_п2 = –(E_п2 – E_п1).

При изменении положения тела изменяется его потенциальная энергия. Таким образом,

работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком.

Знак «минус» означает, что при падении тела сила тяжести совершает положительную работу, а потенциальная энергия тела уменьшается. Если тело движется вверх, то сила тяжести совершает отрицательную работу, а потенциальная энергия тела при этом увеличивается.

4. При определении потенциальной энергии тела необходимо указывать уровень, относительно которого она отсчитывается, называемый нулевым уровнем.

Так, потенциальная энергия мяча, пролетающего над волейбольной сеткой, относительно сетки имеет одно значение, а относительно пола спортзала — другое. При этом важно, что разность потенциальных энергий тела в двух точках не зависит от выбранного нулевого уровня. Это означает, что работа, совершенная за счет потенциальной энергии тела, не зависит от выбора нулевого уровня.

Часто за нулевой уровень при определении потенциальной энергии принимают поверхность Земли. Если тело падает с некоторой высоты на поверхность Земли, то работа силы тяжести равна потенциальной энергии: A = mgh.

Следовательно, потенциальная энергия тела, поднятого на некоторую высоту над нулевым уровнем, равна работе силы тяжести при падении тела с этой высоты до нулевого уровня.

5. Потенциальной энергией обладает любое деформированное тело. При сжатии или растяжении тела оно деформируется, изменяются силы взаимодействия между его частицами и возникает сила упругости.

Пусть правый конец пружины (см. рис. 68) перемещается из точки с координатой Dl₁ в точку с координатой Dl₂. Напомним, что работа силы упругости при этом равна:

A = – .

Величина  = E_п1 характеризует первое состояние деформированного тела и представляет собой его потенциальную энергию в первом состоянии, величина = E_п2 характеризует второе состояние деформированного тела и представляет собой его потенциальную энергию во втором состоянии. Можно записать:

A = –(E_п2 – E_п1), т. е.

работа силы упругости равна изменению потенциальной энергии пружины, взятому с противоположным знаком.

Знак «минус» показывает, что в результате положительной работы, совершенной силой упругости, потенциальная энергия тела уменьшается. При сжатии или растяжении тела под действием внешней силы его потенциальная энергия увеличивается, а сила упругости совершает отрицательную работу.

Потенциальная энергия — механическая энергия системы тел, определяемая их вза­имным расположением и характером сил взаимодействия между ними. Пусть взаимодействие тел осуществляется посредством силовых полей (например, поля упругих сил, поля гравитационных сил), характеризующихся тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Такие поля называются потенциальными, а силы, действующие в них, — консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипатнвной; ее примером является сила трения. Тело, находясь в потенциальном поле сил, обладает потенциальной энергией П. Работа консервативных сил при элементарном (бесконечно малом) изменении кон­фигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:   (12.2) Работа dA выражается как скалярное произведение силы F на перемещение dr и выражение (12.2) можно записать в виде   (12.3) Следовательно, если известна функция П(r), то из формулы (12.3) можно найти силу F по модулю и направлению. Потенциальная энергия может быть определена исходя из (12.3) как где С — постоянная интегрирования, т. е. потенциальная энергия определяется с точ­ностью до некоторой произвольной постоянной. Это, однако, не отражается на физи­ческих законах, так как в них входит или разность потенциальных энергий в двух положениях тела, или производная П по координатам. Поэтому потенциальную энер­гию тела в каком-то определенном положении считают равной нулю (выбирают нулевой уровень отсчета), а энергию тела в других положениях отсчитывают от­носительно нулевого уровня. Для консервативных сил 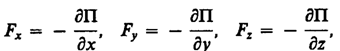или в векторном виде   (12.4)

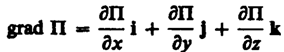
(12.5) (i, j, k — единичные векторы координатных осей). Вектор, определяемый выражением (12.5), называется градиентом скаляра П. Для него наряду с обозначением grad П применяется также обозначение ÑП. Ñ («набла») означает символический вектор, называемый оператором Гамильтона* или набла-оператором: 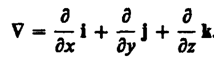(12.6)

19. есть в .pdf

Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы сохраняется. В классической механике при этом пренебрегают деформациями тел. Соответственно, считается, что энергия на деформации не теряется, а взаимодействие распространяется по всему телу мгновенно. Хорошей моделью абсолютно упругого удара является столкновение бильярдных шаров или упругих мячиков. Математическая модель абсолютно упругого удара работает примерно следующим образом:

1. Есть в наличии два абсолютно твердых тела, которые сталкиваются

2. В точке контакта происходят упругие деформации. Кинетическая энергия движущихся тел мгновенно переходит в энергию деформации.

3. В следующий момент деформированные тела принимают свою прежнюю форму, а энергия деформации вновь переходит в кинетическую энергию.

4. Контакт тел прекращается и они продолжают движение.

Для математического описания простейших абсолютно упругих ударов, используется закон сохранения энергии и закон сохранения импульса.

Здесь m₁, m₂ - массы первого и второго тел. u₁, v₁ - скорость первого тела до, и после взаимодействия. u₂, v₂ - скорость второго тела до, и после взаимодействия.

Важно - импульсы складываются векторно, а энергии скалярно.