13.Линейнозависимые и линейнонезависимые векторы. Базис

Рассмотрим алименты x1, x2, xn (1) линейного пространства V.

y=₁x1+₂x₂+…+_nx_n,  принадлежит R.

Система векторов (1) линейно зависима, если

₁x1+₂x₂+…+_nx_n = 0, при этом хотя бы одно не равно нулю.

Система векторов (1) линейно независимой, если

₁x1+₂x₂+…+_nx_n = 0, при всех  = 0.

Если система векторов линейно зависима, то хотя бы одно  выражается через остальные.

1 Всякая система векторов, имеющая нулевой вектор – линейно зависима.

2 Если К векторов (К<n) системы (1) линейно зависима, то и система (1) линейно зависима.

3 Если из системы линейно независимых векторов отбросить r векторов (r<n), то оставшаяся система линейно независима.

4 Если среди векторов системы (1) имеются такие x_k и x_n, что x_k=x_n, то система линейно зависима.

5 Векторы x1+x₂+…+x_n линейно зависимы т. и т.т., когда один из векторов является линейной комбинацией остальных.

Пусть n – натуральное число. Линейное пространство V называется n-мерным, если в нем существуют n линейно независимых векторов, а всякие (n+1) линейно зависимы. n-называется размерность линейного пространства. обозначается dimV. Если пространство нулевое, то его размерность = 0. обозначается dimV.

Базисом n- мерного пространства называется любая упорядоченная система n-линейно независимых векторов.

14.Скалярное произведение векторов и его свойства.

Скалярным произведением двух ненулевых векторов называется число, равное произведению этих векторов на косинус угла между ними.

1. 

2. 

3. 

4. 

17. Векторное произведение векторов и его свойства.

Три некомпланарных вектора образуют правую тройку если с конца третьего поворот от первого вектора ко второму совершается против часовой стрелки. Если по часовой – то левую.

Векторным произведением вектора на вектор называется вектор , который:

1. Перпендикулярен векторам и .

2. Имеет длину, численно равную площади параллелограмма, образованного на векторах и .

, где

3. Векторы , и образуют правую тройку векторов.

Свойства:

1. 

2. 

3. 

4. 

19. Смешанное произведение векторов и его свойства.

Смешанное произведение записывают в виде: .

Смысл смешенного произведения: сначала два вектора векторно перемножают, а затем полученный скалярно перемножают с третьим вектором. Смешанное произведение представляет собой число – число. Результат смешанного произведения – объем параллелепипеда, образованного векторами.

Свойства.

1. Смешанное произведение не меняется при циклической перестановке сомножителей:

2. Смешанное произведение не изменится при перемене местами векторного и скалярного произведения.

3. Смешанное произведение меняет знак при перемене мест любых двух векторов-сомножителей.

4. Смешанное произведение трех ненулевых векторов равно нулю тогда и только тогда, когда они компланарны.

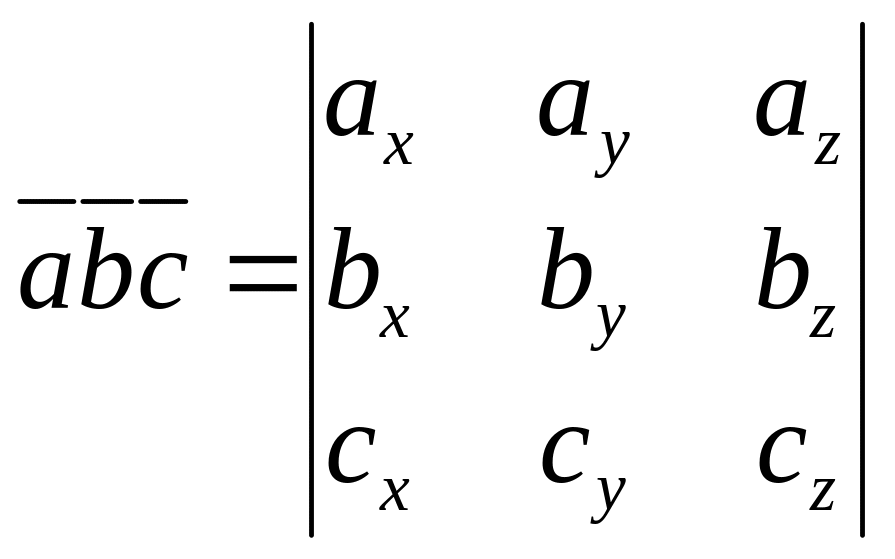
Три вектора называются компланарными, если результат смешанного произведения равен нулю.