35. Математические модели сигналов с ограниченным спектром. Примеры: сигналы после идеального фильтра нч и после идеального полосового фильтра.
Теоретически для полного восстановления сигнала по его спектру необходимо учитывать все спектральные составляющие, лежащие в интервале от 0 до (по частоте). Физически такая процедура неосуществима, так как реальные системы имеют ограниченную полосу пропускания. Но часто и нет необходимости учитывать все спектральные компоненты, поскольку высшие гармоники в спектре имеют малую энергию вследствие свойств самих сигналов. Поэтому важно рассмотрение сигналов с ограниченным спектром:
.
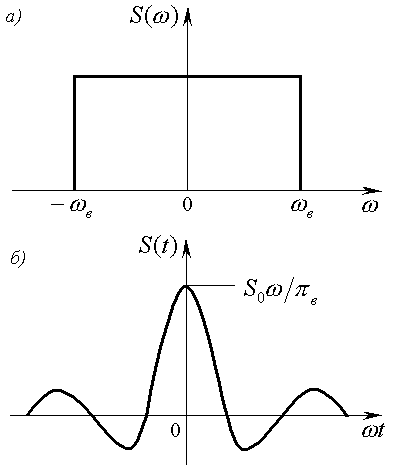(1)
Оригинал такой функции в силу четности спектра аналитически записывается так:
.
(2)
График функции, построенный по формуле (2), показан на рисунке б.
Такой сигнал называется идеальным НЧ
сигналом. Теоретически такой сигнал
может быть получен при прохождении
-импульса
через идеальный НЧ фильтр.
Другим примером сигнала с ограниченным спектром может служить идеальный полосовой сигнал, показанный на рисунке а ниже.
.
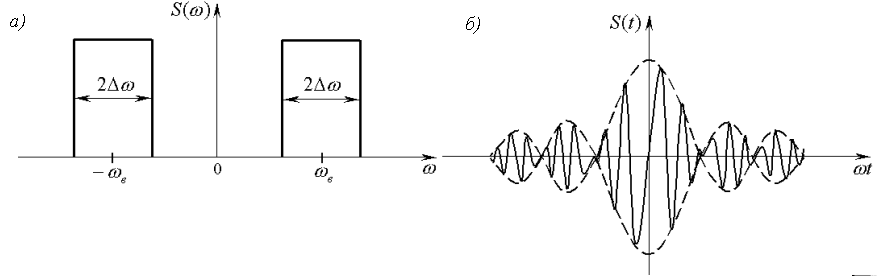
(3)
Используя свойство четности для каждой
из полос спектра и свойства суммы
спектров найдем оригинал функции
:
.
(4)
36. Ортогональные сигналы с ограниченным спектром. Скалярное произведение ортогональных сигналов. Разложение по функциям котельникова.
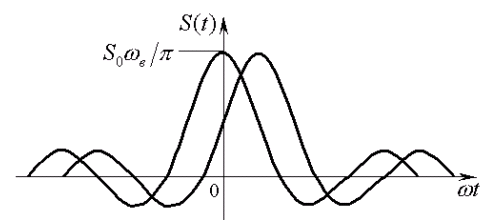
Ортогональные сигналы с ограниченным
спектром. Рассмотрим два идеальных
НЧ сигнала, имеющих одинаковые параметры
,
и отличающиеся тем, что один из них
сдвинут на время
.
,
(
);
,
(
).
(1)
Скалярное произведение этих сигналов:
.
(2)
Для ортогональных сигналов скалярное
произведение равно нулю. Для двух
рассмотренных сигналов это условие
выполняется, если
(
).
Минимальный возможный сдвиг, при котором
наблюдается ортогональность, при
.
Таким образом, показано, что получен бесконечный ортогональный базис, позволяющий разложение произвольного сигнала, спектр которого отсутствует.
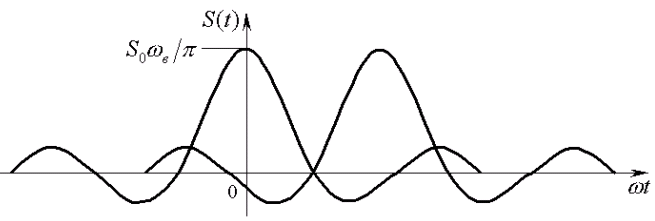
Теорема и ряд Котельникова.
Теорема: любую функцию времени
,
имеющую ограниченный спектр, сосредоточенный
в полосе от 0 до
,
где
–
максимальная частота спектра, можно
передать с любой точностью при помощи
отсчетов функции, отстоящих на время
не более
.
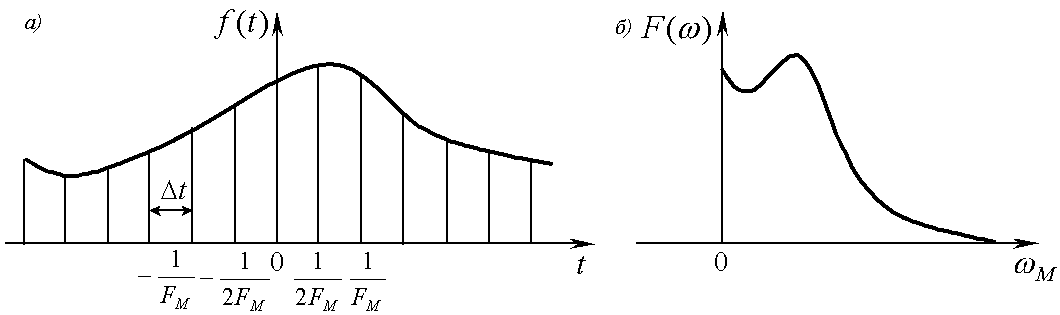
Содержание теоремы иллюстрируется на
рисунке, где на рисунке а показана
временная функция, а на рисунке б
показан ее спектр
,
ограниченный частотой
.
Такая функция может быть с какой угодно
точностью передана с помощью отсчетов,
отстоящих друг от друга на время
.
Доказательство: любая функция может быть задана с помощью своего спектра соотношением:
,
(3)
или с учетом ограниченности полосы пропускания сигнала записью:
.
(4)
Формально функцию
на интервале от
до
можно представить в виде ряда Фурье (с
периодом
),
только при этом следует иметь в виду
существенную особенность ряда, что в
качестве аргумента переменной
выступает
,
то есть
в данном случае запишется в виде:
.
(5)
В отличие от формулы для
в ряде Фурье для функции
независимая переменная
заменена на
.
А величина
,
характеризующая периодичность сигнала
заменена величиной
.
Подставляя в формулу (4) значение , выраженное рядом (5), приходим к следующей записи:
.
(6)
.
Используя формулу Эйлера, получим
следующее выражение для
:
.
И тогда формула (6) перепишется:
.
(7)
Таким образом, получаем разложение в
ряд произвольной функции по ортогональному
базису, представленному функциями
,
и (2).
В ряде Фурье коэффициенты ряда выражаются через разлагаемую в ряд функцию с помощью известной формулы:
.
(8)
В нашем случае с учетом замены на в формуле (5), получим:
.
(9)
В формуле (4) зададим
дискретными значениями
.
Тогда получим:
.
(10)
В полученных записях выражение для
интегралов совпадают. Поэтому, если
разделить левые и правые части двух
последних равенств друг на друга и
решить относительно
,
то получим:
.
Подставляя полученные выражения
в формулу (7), получим:
.
Или учитывая, что суммирование ведется
по всем положительным и отрицательным
значениям
,
то окончательно можно записать:
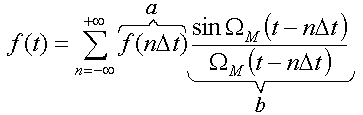(11)
Полученное выражение называется рядом
Котельникова. Значения
называют отсчетами функции (множитель
в функции отсчетов).
Таким образом, доказано, что произвольный
сигнал, спектр которого не содержит
частот выше
может быть полностью восстановлен, если
известны отсчеты этого сигнала, взятые
через равные промежутки
.
Элементарный сигнал с ограниченной полосой пропускания, как видно в сравнении с рядом, представляет собой одну из компонент ортогонального базиса, составляющего основу ряда.
Теорема Котельникова, доказанная в 1933 г., является фундаментальным положением радиотехники и устанавливает возможность точного восстановления сигнала с ограниченным спектром по его выборкам, взятым через равные промежутки времени.