Виды информации и их представление в компьютере
Классификация видов информации
Человек воспринимает окружающий мир с помощью органов чувств. Поэтому существует классификация видов информации по восприятию человеком:
1. Визуальная информация (около 90% всей воспринимаемой информации).
2. Аудиальная (слуховая) (около 9% всей воспринимаемой информации) информация.
3. Тактильная информация.
4. Обонятельная информация.
5. Вкусовая информация.
Отметим, что человек может воспринимать информацию, как в аналоговой, так и в дискретной форме.
На настоящий момент компьютер может достаточно качественно передавать визуальную и аудиальную информацию. Частично передается тактильная информация (особенно в игровой индустрии – рули с обратной связью и т.д.), но говорить о передаче любого типа информации пока преждевременно. При этом для представления в компьютере используется дискретный способ представления информации.
По особенностям компьютерного представления информации принято выделять следующие виды:
1. Числовая
2. Текстовая
3. Графическая
4. Звуковая
5. Комбинированная (видеоинформация)
Отметим, что каждое последующее представление информации возникало позже предыдущего и так или иначе было основано на представлении числовой информации. Следовательно, в память компьютера может быть записана только числовая информация, а затем компьютеру необходимо объяснить, как следует трактовать записанные в памяти числа. Данное обстоятельство является ключевым в области современных информационных технологий и позволяет создавать универсальные устройства путем разделения двух принципиально различных задач: хранения информации и ее представления. Например, большинство современных устройств (мобильные телефоны, карты памяти фото и видеотехники и т.д.) позволяет не только хранить и качественно обрабатывать только свою информацию, но и может использоваться в качестве просто носителей информации. Хотя при этом само устройство возможно и не сможет работать с этой информацией. Например, записав в память фотоаппарата текстовый файл, мы гарантированно перенесем его на свой компьютер, но не обязательно фотоаппарат позволит просмотреть или обработать этот файл.
Представление же информации по своей сути является некоторым алгоритмом, который объясняет, как нужно интерпретировать хранящиеся данные. Появление языка Java и распространение программ на этом языке позволили оснастить многие мобильные устройства приложениями, работающими с различными типами информации. Ключевой особенностью является то, что можно самостоятельно написать приложение на этом языке и расширить функциональные возможности своего телефона, плеера и т.д.
Вывод: Дискретный способ представления информации позволяет сделать универсальным хранение информации любого вида, а применение языков типа Java позволяет по-разному интерпретировать хранящиеся данные. В связи с чем, компьютеры и современные мобильные устройства являются универсальными устройствами для работы с практически любыми видами информации.
Аналоговая и дискретная информация
Выше уже указывалось, что существуют две принципиально различные формы представления информации: аналоговая и дискретная, а также указывалось, что в современной микропроцессорной технике используется дискретная форма представления. Рассмотрим, в чем принципиальные отличия этих форм и как они могут быть преобразованы друг в друга.
Все природные процессы и явления носят аналоговую, т.е. непрерывную форму. Дискретная форма появилась в процессе деятельности человека. Принципиальным отличием дискретной формы является то, что информация представляется не непрерывно, а в виде последовательности некоторых знаков или сигналов из некоторого КОНЕЧНОГО набора. Например, конспект является дискретной формой представления, т.к. это в определенном порядке записанная последовательность знаков алфавита. При дискретном способе представления каждый сигнал можно отделить от другого и обозначить.
Очевидно, что можно выделить 4 типа преобразования:
аналоговая форма -> аналоговая форма. Такое преобразование осуществляется например в мегафоне. Путем воздействия на мембрану микрофона звуковая волна вызывает соответствующие электромагнитные волны, которые после усиления передаются на мембрану динамика и снова порождают звуковые волны, но уже более сильные. Все эти процессы относятся к естественным природным процессам и имеют аналоговый характер. В любом процессе преобразования могут возникнуть помехи. В данном случае исходный сигнал мог иметь абсолютно произвольное значение величины сигнала (т.к. имеет аналоговую форму представления) и соответственно нельзя проверить был ли этот сигнал искажен в процессе преобразования или нет.
дискретная форма -> дискретная форма. Такое преобразование называется перекодировкой и очевидно может быть выполнено без помех. В случае возникновения помех они легко обнаруживаются и устраняются. Примерами таких преобразований могут выступать различные коды замены, когда один символ заменяется на другой по определенному правилу: код Цезаря, Вижернера и т.д.
аналоговая форма -> дискретная форма. Такое преобразование называется оцифровкой и применятся при сведении любой естественной информации к компьютерному представлению. В таком случае наблюдение за аналоговым сигналом осуществляется не постоянно, а в некоторые моменты времени через одинаковые промежутки. Считается, что до следующего измерения величина сигнала не изменяется. При этом величина сигнала измеряется не точно, а только с определенным шагом. Такое преобразование представлено на рисунке, где непрерывная функция заменяется на соответствующие точки в узлах сетки оцифровки.
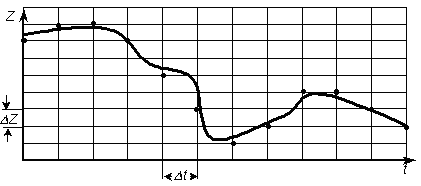
Рис. Оцифровка аналогового сигнала.
Разбивка временного интервала на отрезки называется дискретизацией по времени, а разбивка шкалы измерения сигнала на отрезки – квантованием по величине.
дискретная форма -> аналоговая форма. Такое преобразование называется восстановлением и является обратным к рассмотренному выше. Возникает, например, при прослушивании музыки, записанной в цифровой форме. Очевидно, что чем меньше шаг квантования и дискретизации, тем более точно ступенчатая функция приближает непрерывную. Ответом на вопрос может ли дискретная форма точно отображать аналоговую является теорема Котельникова (теорема отсчетов):
Непрерывный сигнал можно полностью отобразить и точно воссоздать по последовательности измерений или отсчетов величины этого сигнала через одинаковые интервалы времени, меньшие или равные половине периода максимальной частоты, имеющейся в сигнале
Теорема справедлива потому, что любое естественно или техническое устройство, воспринимающее информацию, имеет верхний и нижний пороги чувствительности, а также шаг чувствительности. Если человеку показать два близких друг к другу цвета, то он не всегда их сможет различить. Такой порог у каждого человека свой, но тем не менее можно выбрать такой порог, когда ни один человек не сможет различить эти цвета. Данное утверждение справедливо и для технических устройств. Например, для точной передачи речевого сигнала должно производиться не менее 8000 отсчетов в секунду; для точной передачи телевизионного сигнала потребуется около 8000000 отсчетов в секунду.
Таким образом, дискретная форма может точно отображать аналоговую и при этом все преобразования могут быть выполнены точно. Данное обстоятельство и сделало приоритетным дискретное представление информации в памяти современных устройств.
Числовая информация
Естественное, что компьютер и все устройства, которые являлись его предшественниками, в первую очередь должны были автоматизировать вычислительный процесс. Слова «компьютер» и «калькулятор» могут быть переведены как «вычислитель». Русскоязычный термин ЭВМ (электронно-вычислительная машина) также в явной форме отражает основное назначение – вычисления. Как и было отмечено выше любой другой вид информации будет сводиться к числовой. Поэтому числовая информация имеет особое значение и как следствие множество способов представления.
Числовая информация делится на:
Целые числа, которые в свою очередь на:
числа со знаком;
числа без знака.
Вещественные числа.
Числа без знака
Используются для представления только положительных чисел. В зависимости от отводимого объема памяти варьируется и диапазон возможных значений. При представлении чисел без знака все разряды, отводимые под число, используются для хранения величины этого числа. Следовательно, количество бит памяти и диапазон значений связаны соотношением:
где N – количество бит памяти, отводимых под хранение числа.
В языке Паскаль среди целочисленных типов данных используются следующие:
Название типа |
Объем памяти |
Диапазон значений |
Byte |
1 байт (8 бит) |
0..255 |
Word |
2 байта (16 бит) |
0..65535 |
Для получения компьютерного представления числа без знака достаточно перевести это число в двоичную систему счисления и записать в необходимое количество разрядов (8 или 16) дополнив слева это число незначащими нулями.
Пример: получить компьютерное представление числа 29 в виде целого числа без знака (8 бит).
Переводим число 29 в двоичную систему счисления: 11101 а затем дописываем слева незначащими нулями до 8 разрядов: 00011101. Это и есть искомое компьютерное представление.
Для получения числа по его компьютерному представлению достаточно просто перевести это представление в десятичную систему счисления.
Пример: Дано компьютерное 8 битное представление целого числа без знака: 00101110. Определить какое это число.
Переведем число 00101110 из двоичной системы счисления в десятичную: 46. Это и есть ответ.
Числа со знаком
Используются для представления как положительных, так и отрицательных чисел. При представлении чисел со знаком один бит в явной или неявной форме отводится под хранение знака числа, соответственно под значение величины числа отводится на 1 бит меньше, чем в представлении чисел без знака.
Следовательно, количество бит памяти и диапазон значений связаны соотношением:
где N – количество бит памяти, отводимых под хранение числа.
В языке Паскаль среди целочисленных типов данных используются следующие:
Название типа |
Объем памяти |
Диапазон значений |
ShortInt |
1 байт (8 бит) |
-128..127 |
Integer |
2 байта (16 бит) |
-32768..32767 |
LongInt |
4 байта (32 бита) |
-2 147 483 648..2 147 483 647 |
Числа со знаком хранятся в памяти компьютера в дополнительном коде. Дополнительных код получается по правилу:
Для положительного числа прямой код равен обратному и равен дополнительному.
Для отрицательных чисел:
Прямой код это запись модуля числа в двоичной системе счисления в необходимое количество разрядов.
Обратный код это инверсия прямого кода (1 заменяются на 0 и наоборот).
Дополнительный код это прибавление к обратному коду числа величины 1 по математическим правилам.
Пример: Получить компьютерное представление в виде числа со знаком (8 бит): 90, -45.
Число 90 является положительным числом, поэтому достаточно просто перевести это число в двоичную систему счисления и записать в 8 разрядов: 01011010.
Число -45 является отрицательным поэтому:
сначала необходимо перевести модуль числа в двоичную систему счисления и записать в 8 разрядов: 00101101;
затем инвертировать полученный на предыдущем шаге результат: 11010010;
добавить по математическим правилам к результату инверсии число 1: 11010011.
Полученное число 11010011 и является 8-битным представлением числа -45 в виде числа со знаком.
Для обратного преобразования (из компьютерного представления определить число) необходимо знать какое это число по знаку (положительное или отрицательное). Признаком знака числа является старший бит. Если старший бит равен 1, то число отрицательное, в противном случае – число положительное. В зависимости от знака числа в обратном порядке выполняются все действия, рассмотренные выше.
Пример: Определить какие числа имеют представления: 10010010 и 00110011.
Т.к. старший бит в представлении числа 10010010 равен 1, то значит число является отрицательным. Следовательно, для получения значения числа необходимо:
вычесть по математическим правилам из данного представления 1: 10010001;
инвертировать полученный на предыдущем шаге результат: 01101110;
перевести результат инверсии из двоичной системы в десятичную и записать со знаком «-»: -110.
Во втором представлении 00110011 старший бит равен 0, следовательно число является положительным. Поэтому достаточно просто перевести это представление в десятичную систему счисления: 51.
Вещественные числа
Можно предложить 2 принципиально различных способа представления вещественных чисел:
с фиксированной точкой, когда хранится отдельно целая и отдельно дробная часть числа;
с плавающей точкой, когда число разбивается на мантиссу и порядок.
Представление в виде «с плавающей точкой» (мантиссаЕпорядок) читается как произведение мантиссы числа на основание системы, возведенное в указанный порядок. Для десятичной системы это выглядит как:
мантисса·10порядок.
Представление с фиксированной точкой удобно для восприятия человеком, но приводит к существенным ограничениям диапазонов хранимых чисел. Кроме того, представление с фиксированной точкой плохо подходит для записи очень больших и очень малых чисел. В связи с чем, в компьютере используется представление вещественного числа с плавающей точкой.
Примером представления числа в виде «с плавающей точкой» являются записи:
17512Е-2, 1.7512Е2, 175.12Е0, 0.17512Е3.
Все эти представления относятся к одному и тому же числу 175,12.
Из приведенного примера ясно, что такое представление не является однозначным, поэтому необходимо добавить условие, позволяющее однозначно получать представление для каждого числа. Таким условием является нормализованная форма записи числа. При нормализованной записи необходимо чтобы мантисса была представлена в виде правильной дроби, т.е. целая часть равна 0, а первая цифра после запятой была отлична от 0. В приведенных примерах нормализованной записью является 0.17512Е3.
Существует несколько различных представлений вещественных чисел. Как правило, они отличаются диапазоном и точностью представления. Рассмотрим представление вещественных чисел на примере величины типа Double (двойная точность), используемой в языке Pascal. Такое представление позволяет записывать числа из диапазона от 5.0е-324 до 1.7е308… с точностью до 15-16 разрядов.
Для рассматриваемого представления используется 64 бита (8 байт), разделенные на 3 логические группы:
1 группа состоит из 1 старшего бита в представлении (63 бит). Эта группа отвечает за знак числа (1- отрицательное, 0 – положительное)
2 группа состоит из 11 разрядов (с 52 по 62 биты). Эта группа отвечает за «смещенный» порядок числа
3 группа состоит из 52 разрядов (с 0 по 51 биты). Группа отвечает за мантиссу числа.
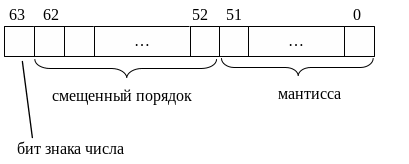
Рис. Схематическое представление величины типа Double.
Алгоритм получения компьютерного представления величины типа Double
1. Перевести модуль числа в двоичную систему счисления и записать результат в нормализованной форме. При этом под нормализованной формой будем понимать такую запись, при которой целая часть числа равна 1. В этом случае можно сэкономить один разряд (не хранить его явно, но подразумевать его существование).
2. К порядку числа, полученному на предыдущем шаге добавить величину 1023 и записать результат в виде 11-битного двоичного числа. Эта величина называется «смещенным» порядком.
3. Записать результат по схеме, представленной на рисунке: знак числа (1 – если число отрицательное или 0 – если число положительное), затем «смещенный порядок» и мантиссу. Для удобства восприятия получившееся 64-битное двоичное число переводят в шестнадцатеричную систему.
Пример: Получить компьютерное представление числа 125,125 в виде величины типа Double.
В соответствии с алгоритмом переведем это число в двоичную систему счисления: 1111101,0012.
Это же число в нормализованной форме будет записано как: 1,111101001∙26. Жирным курсивом выделены элементы результата, которые будут использоваться дальше.
Смещенный порядок равен 6+1023=1029, что в двоичной системе счисления будет записано как: 10000000101.
Запишем результат по схеме.
Получим: 0 10000000101 1111010010000000000000000000000000000000000000000000
Для удобства восприятия запишем результат в 16-ричной системе счисления: 405F480000000000
Алгоритм получения величины числа по компьютерному представлению.
1. При необходимости перевести число в двоичную систему и разбить на группы.
2. Группу, отвечающую за «смещенный» порядок перевести в десятичную систему счисления и вычесть число 1023.
3. Записать мантиссу с учетом хранящейся дробной части и подразумеваемой 1 и умножить ее на 2 в степени, вычисленной в п.2. алгоритма (переместить запятую на указанное количество разрядов).
4. Перевести число из двоичной в десятичную систему и записать его с учетом знака.
Пример: Определить величину числа, если его компьютерное представление имеет вид: C03774BC00000000
Переведем это число в двоичную систему и запишем, разбив на группы:
1 10000000011 0111011101001011110000000000000000000000000000000000
В старшем бите хранится 1, следовательно число отрицательное.
В группе смещенного порядка хранится число: 10000000011, что соответствует числу 1027. Соответственно порядок числа равен: 1027-1023=4.
Теперь можно записать число в двоичной системе счисления: 1,011101110100101111∙24 = 10111,01110100101111 23,456. Следовательно, это число (-23,456).
Текстовая информация
Для хранения текстовой информации в памяти компьютера используются специальные кодировочные таблицы, которые ставят в соответствие каждому символу некоторый числовой код. Широкое применение получила кодовая таблица ASCII, состоящая из 256 символов. Первая часть кодовой таблицы (символы с кодами от 0 до 127) является универсальной и используется для хранения специальных управляющих символов и символов латинского алфавита. Использование символов из этой части обеспечивает гарантированное представление информации на всех компьютерах во всем мире. Вторая часть таблицы (символы с кодами от 128 до 256) является национальной или альтернативной. Эта часть используется для представления символов национальных алфавитов, символов псевдографики и т.д. Использование символов из этой части может привести к нечитаемости текстовой информации. Такая проблема часто возникала при отправке электронных писем в другие страны. Например, набирая текст письма русскими буквами в России, формировался соответствующий текстовый документ с кодами ASCII, входящими в альтернативную кодовую часть. Сам документ естественно просматривался без проблем, но при отправке письма, например, в Германию, где используется другая альтернативная часть, письмо не читалось. Поэтому для гарантированного прочтения стали использоваться символы латиницы, но само слово писалось так, как оно записывается по-русски. Такой подход породил так называемый транслит, который сейчас широко распространен в сети Internet. Нечитаемость сообщения объясняется тем, что реально запоминаются не символы, набираемые на клавиатуре, а их коды. При воссоздании символов по их кодам с использованием другой кодовой таблицы очевидно и получается нечитаемое сообщение. Кроме того, даже в России существовало несколько кодовых таблиц для альтернативной части (IBM CP866, KOI8-R, CP1125 и т.д.), что также приводило к нежелательным последствиям. С такой ситуацией Вы встречались, просматривая Web-страницы не в той кодировке. Но после выбора нужной кодировки все становилось на свои места. Тем не менее, кодовая таблица ASCII до сих пор применяется потому, что для хранения кода одного символа используется всего 8 бит (1 байт) памяти. Это одновременно и достоинство и недостаток таблицы. С одной стороны это удобно – объем текстового файла получается равным количеству символов в тексте. Кроме того, такое представление является минимальным. Но с другой стороны с помощью 8 бит можно закодировать всего 256 различных символов, что и становится существенным недостатком, т.к. нельзя в рамках одной таблицы закодировать символы хотя бы наиболее распространенных алфавитов.
Выходом из этой ситуации является применение кодовой таблицы Unicode, предложенной в 1991 г. ( http://www.unicode.org/charts/). В этой кодовой таблице для хранения кода символа используется 2 байта (16 бит) памяти, что позволяет закодировать 65 536 различных символов. Такого количества достаточно для всех существующих в настоящий момент алфавитов и еще остается существенный запас. Естественно при этом объем файла по сравнению с ASCII-кодировкой увеличивается вдвое, т.к. каждый символ занимает не 1, а 2 байта памяти. Для совместимости с ASCII первые 128 символов обеих таблиц совпадают. Для национальных алфавитов выделенные определенные области таблицы Unicode. На рис. представлены символы кириллицы и их коды в соответствии со стандартом Unicode 5.1.
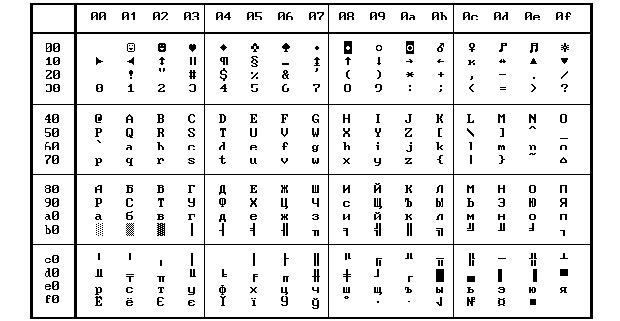
Рис. Таблица ASCII.
Рис. Область кириллических символов таблицы Unicode.
Само преобразование текстовой информации в компьютерное представление не вызывает никаких проблем. Каждый символ сообщения, включая пробелы, знаки пунктуации и т.д. по соответствующей кодовой таблице заменяется на числовой код.
Пример: Получить компьютерное представление фразы «Знание – сила!» с помощью кодовой таблицы ASCII.
Используя кодовую таблицу ASCII найдем каждую букву текста и заменим ее на сумму номера строки и столбца: «87 AD A0 AD A8 A5 20 2D 20 E1 A8 AB A0 21»
Для обратного преобразования необходимо компьютерное представление разбить на отдельные блоки (по 8 бит для ASCII-кодировки или 16 бит для Unicode-кодировки), а затем каждый блок независимо декодировать по кодовой таблице.
Пример: Декодировать сообщение «88 20 AE AF EB E2 2C 20 E1 EB AD 20 AE E8 A8 A1 AE AA 20 E2 E0 E3 A4 AD EB E5 2C 20 88 20 A3 A5 AD A8 A9 20 2D 20 AF A0 E0 A0 A4 AE AA E1 AE A2 20 A4 E0 E3 A3 2E».
Решение: Т.к. сообщение кодирование осуществлялось с помощью таблицы ASCII, то необходимо каждое число разбить на отдельные цифры: первая цифра определяет номер столбца, а вторая – номер строки. На пересечении соответствующей строки и столбца и будет находится искомый символ. Число 88 – дает строку с номером 8 и столбец с номером 8. На пересечении этой строки и столбца находится символ «И». Следующий код 20 декодируется как символ « » (пробел), стоящий на пересечении строки с номером 2 и столбца с номером 0. Проводя процесс далее получим все фразу «И опыт, сын ошибок трудных, И гений – парадоксов друг.».
Графическая информация
С точки зрения компьютерного представления выделяют 3 вида графической информации:
Растровая графика. Все изображение разбивается на ряд элементарных объектов – пикселей, каждый из которых имеет один определенный цвет. В памяти компьютера при этом хранится код цвета каждого пикселя. Общего представления о том, что содержится в рисунке, компьютер не имеет.
Векторная графика. Все изображение строится из некоторых фигур, контуры которых описываются кривыми Безье. При таком способе построения рисунка запоминается последовательность действий пользователя. Рисунок легко может быть увеличен или уменьшен без потери качества изображения. Для задания точки на кривой Безье достаточно 4 чисел. Следовательно, и в этом случае графическая информация сводится к числовой.
Фрактальная графика. Изображение строится на основе формулы.
Достоинства и недостатки каждого вида графики подробно рассматриваются в курсе «Программное обеспечение ЭВМ». С практической точки зрения наибольший интерес представляет растровая графика. Для этого необходимо предложить универсальный способ числового кодирования цвета. На самом деле существует большое количество цветовых палитр, позволяющих свести цвет к некоторой числовой информации. Все эти палитры, как правило, широко применяются в различных графических редакторах и рассматриваются при изучении компьютерной графики. Мы рассмотрим один из наиболее распространенных способов кодирования с помощью палитры RGB.
С помощью палитры RGB каждый цвет получается путем интеграции трех базовых цветов: красного, зеленого и синего. При этом, очевидно, достаточно хранить интенсивности этих базовых цветов. В зависимости от отводимого под хранение каждого пикселя объема памяти будет отличаться и общее количество цветов, которое можно использовать в изображении. Объем памяти, отводимый под хранение кода цвета одного пикселя изображения, называется битовой глубиной цвета. Битовая глубина цвета (i) и максимальное количество цветов (N) связаны соотношением:
Рассмотрим наиболее типичные битовые глубины цвета и оценим количество цветов, возникающих при таком кодировании.
1 бит. Цветного изображения в этом случае получить нельзя, т.к. с помощью 1 бита можно закодировать только 2 цвета. Обычно это черный и белый.
4 бита. Такое представление используется при программировании графики с помощью языка Pascal и позволяет закодировать 16 различных цветов. Каждому базовому цвету отводится по 1 биту. Если в этом бите стоит 1, то значит данная составляющая присутствует в кодируемом цвете, в противном случае – нет. Оставшийся бит используется для придания яркости всем входящим в цвет компонентам. Палитра кстати и делится на 2 части: темную (с кодами от 0 до 7) и яркую (с кодами от 8 до 15):
Темные цвета |
Светлые цвета |
||||
Константа |
Число |
Цвет |
Константа |
Число |
Цвет |
Black |
0 |
Черный |
DarkGray |
8 |
Темно-серый |
Blue |
1 |
Синий |
LightBlue |
9 |
Ярко-синий |
Green |
2 |
Зеленый |
LightGreen |
10 |
Ярко-зеленый |
Cyan |
3 |
Голубой |
LightCyan |
11 |
Ярко-голубой |
Red |
4 |
Красный |
LightRed |
12 |
Ярко-красный |
Magenta |
5 |
Фиолетовый |
LightMagena |
13 |
Ярко-фиолетовый |
Brown |
6 |
Коричневый |
Yellow |
14 |
Желтый |
8 бит. Представление используется в безопасном режиме Windows, а также в ряде графических форматов типа bmp и gif. Данное представление позволяет закодировать 256 цветов.
При распределении бит между базовыми цветами по 3 бита получили красный и зеленый цвет и 2 бита – синий. Это обусловлено тем, что человек в наименьшей степени может различить интенсивность синей составляющей.
24 бита. (3 байта) Позволяет закодировать 16 777 216 цветов. Под каждую составляющую отводится 8 бит, что позволяет закодировать по 256 интенсивностей каждого базового цвета. По данным физиологов человеческий глаз способен различить до 17 миллионов оттенков, поэтому данное представление практически перекрывает возможности человеческого зрения.