5. Гидравлический расчет трубопроводов.

Гидравлическая система в жид-ть передается ч/з трубопровод (нефте- и газо трубопровод, системы водоснабжения). Жид-ть может двигаться за счет того, что пот. эн. в начале больше чем в конце. Разность пот. эн. затрачивается на преодоление гидравлического сопротивления и на изменение кинетической энергии. Повыш. пот. эн. в начале трубопровода может создаваться: 1) за счет насосов; 2) повышения давления на свободной поверхности байки; 3) за счет разности уровня.

Методика расчета одинакова.

Трубопроводы разделяются на простые (постоянного сечения без разветвлений) и сложное (различного диаметра, с разветвлениями).

Формула Бернулли, экспериментальные данные.

Лекция 5

1. Простой трубопровод

Пусть простой трубопровод расположен произвольно в пространстве. Имеет общую длину l, диаметр d, местное сопротивление ξ₁, ξ₂, ξ₃, ξ₄ и t₁ t₂. Пусть протекает жидкость, плотность которой и коэффициент кинем. Вязкости нам известны. Запишем уравнение Бернулли для сечений 1 и 2. Т.к. трубопровод имеет постоянный диаметр, то скорость можно рассчитать U₁=U₂, будем считать, что α₁=α₂.

Уравнение Бернулли:

, (1)

Где - сумма гидравлических сопротивлений

ξтруб – коэффициент сопротивления всей трубы

- потребляемый напор

- распол.напор

(2)

Q-объемный расход

с и ^m – коэффициенты для ламинарного и турбулентного течения

Для ламинарного течения: ; ;

Подставив эти значения можно получить:

(3) m=1

Для турбулентного течения: (4) m=2

Характеристикой трубопровода наз-ся зависимость потребного напором от расхода жидкости.

Для ламинарного течения (т.к.m=1) будем иметь:

Порядок расчета для простого трубопровода зависит от постановки задач.

1. Q, ρ, ν, размеры трубопровода, шероховатость, z₁ и z₂. Определить H_потр.

Последовательность:

1. Определить число Re: , где

2. Определить коэффициент местных сопротивлений: ξi

3. Определить Н_потр по формулам 2, 3 или 4.

2. Даны свойства жидкости (ρ, ν), размеры трубопровода, шероховатость, типы местных сопротивлений, Н_расп. Определить объемный расход (Q).

Граф. аналитический метод:

1. Задается произвольно ряд значений Q.

2. Для каждого Q определяется: Re, коэффициенты местных сопротивлений, коэф.тр., Н_потр, как в задаче 1.

3. Строится характеристика трубопровода.

Н_расп мы имеем точку пересечения Н_расп и Н_потр даст значение Q.

3. Задан Q, ρ, ν, типы местных сопротивлений, размеры трубопровода кроме d, шероховатость, Н_расп. Определить d.

Граф. аналитический метод:

1. Задается ряд значений d.

2. Определяется Re для каждого значения, коэффициент местных сопротивлений, коэффициент потери на трение, потребный напор как в задаче 1.

3. Строится график.

В точке пересечения d.

2. Сложный трубопровод.

1) Последовательно соединенные трубопроводы.

Пусть мы имеем 3 последовательно соединенных трубопровода. Очевидно, что расход проходящий через 1 трубопровод: Q₁=Q₂=Q₃=Q

Потери напора (потери на трение) l_трА-В=l_тр1+l_тр2+l_тр3

Выражение для потр. напора:

(6)

Построим характеристики для 1, 2 и 3 трубопровода.

Т.к. расход для всех трубопроводов одинаковый, то Н_потр определяется сложением.

2) Параллельно соединенные трубопроводы.

Расход которой проходит при параллельно соединенном трубопроводе:

Q=Q₁+Q₂+Q₃ (7)

Суммарная птеря напора исходя из уравнения Бернулли = потере напора в каждом трубопроводе.

(8)

Выразим гидравлические потери через расходы:

(9)

Значение c_i и mi определяем по урав-ниям 3 и 4.

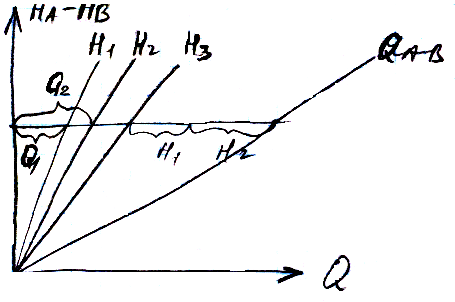
Построим характеристику параллельно соединенных трубопроводов.

Потери напоров в каждом трубопроводе одинаковы поэтому:

Лекция 6