3. Расчет гидравлических потерь в трубах не круглого сечения.

Rr=ПLτ

Rr – сила трения

П – смачиваемый периметр

L - длина

τ – касательные напряжения

Опыты показывают, что расчет … не круглого сечения можно производить по тем же формулам, что и для труб круглого сечения, если d заменить на динамический диаметр.

Гидравлический диаметр

S – площадь поперечного сечения

Местные гидравлические сопротивления при турбулентном течении.

Потери полного напора подсчитываются по формуле Тарси

Задача состоит в том, чтобы определить значение … коэффициент из опытов известно, что при турбулентном режиме _i зависит от вида местного сопротивления и практически не зависит от Re, т.е.потери определяются вихреобразованием. Побочное _i определяется по графикам, таблицам, эмпирическим формулам. При внезапном расширении _i может быть определено аналитически.

При внезапном расширении скорость уменьшается, давление увеличивается, образуется зона обратных токов с вихрем. Случайной называют потерями на удар Борда-Корно:

α₁=α₂=1

α – коэффициент округленности

Из уравнения Бернулли мы можем получить

Из уравнения количества движения можем получить

(P₁-P₂)S₂=G(U₂-U₁)=U₂ρS₂(U₂-U₁)

Уравнение расхода U₂S₂=U₁S₁

Используя записанные уравнения мы можем получить

- теорема Борда-Корно

Потери полного напора равны скоростному напору потерянной скорости

На практике большие потери при внезапном расширении широко используется в логарифмических уплотнениях.

Потери при внезапном сужении рассчитывается по формуле Идельчика

Потери при плавном сужении канала зависит от отношения площадей , ξ колеблется в диапазоне от 0,01 до 0,1.

Потери в отводах – это плавный поворот; потери уменьшаются с увеличением радиуса поворота .

ξ_i - в справочнике (Идельчика)

Эквивалентная длина трубопровода. При расчетах ламинарных движений когда местное сопротивление пропорционально скорости в первой степени потери удобно выражать через эквивалентную длину трубопровода – это длина такого трубопровода заданного диаметром сопротивление которого равно заданному местному сопротивлению.

Суммарные потери в этом случае

4. Истечение жид-ти ч/з отверстие насадки.

Этот процесс широко реализуется на практике при подаче топлива, при подаче воды на лопасти гидротурбин.

Пусть мы имеем ёмкость из которой через отверстие в стенке вытекает жид-ть пот. энергия жид-ти частично превращается в кинетическую, частично затрачивается на приобретение местного сопротивления. Задача состоит в том, чтобы определить скорость U₂ и гидравлич. сопрот. расход. Напор пост, т.е. z₁=const, то можно считать, что U₁=0.

Перепад давлений: P₁+ρgz₁-P₂

Будем считать, что отверстие мало, а стенка тонкая. Частицы обтекая крону, движутся по криволинейным траекториям, что называют центробежными силами направ. к оси, которые сжимают струю d₂<d.

Отношение площадей S2/S называют коэффициентом совершенного сжатия струи

Уравнение Бернулли

Если бы ξ=0, то теор.υ>υ_действ.

H – перепад гидравлических напоров

φ – скоростной коэффициент

Посчитаем расход в сечении 2

ψ – коэф.расхода

φψε – зависят от формы и размеров отверстий

При Re<50 велико значение коэффициента потерь ψ. Коэффициент совершенного сжатия ε – близко к 1. При увеличении Re за счет φ ψ возрастает, достигая максимального значения=0,67 при Re≈350, а затем уменьшатся за счет ε. При Re>5∙10⁴ значение всех коэффициентов приближ.к значению для идеальной жид-ти.

При Re→∞; ξ→0; φ→1; ε=0,61; ψ=0,61;

Для маловязкой жидкости таких как: вода, керосин при больших Re принимают ε=0,63; ξ=0,065; φ=0,97; ψ=0,61;

Часто истечение из отверстия

В этом случае струя сжимается меньше, чем при совершенном сжатии за счет направляющего действия стенок.

ε_н=ε+0,37n², где

Истечение жид-ти ч/з внеш. цилиндрический насадок

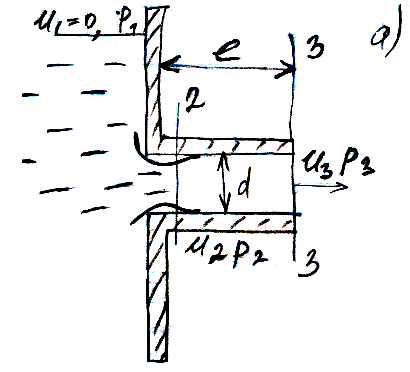
l=(2…6)d

По истечении через насадку возможны 2 случая: а и б.

ε≈1,0; ψ=φ.

Потери напора определяются потерями на удар Берда-Корно м-у сечениями 2 и 3. При Re>10⁴; ε=1,0; ξ=0,5

Потери напора будут > в 7,4, чем при истечении через отверстие тонкой стенки. U₃ меньшев 1,2, за счет дополнительных потерь, расход увеличивается в 3,5 за счет коэффициента универсального сжатия=1.

U₂>в 1,2 т.к.P₂>P₃

При увеличении напора U₂ увеличивается, P₂ уменьшается и при некотором критическом значении P₂ равном pнасыщенных паров начинается кипение и течение переходит в режим б.

P₂ становится=P₃, а истечение становится как истечение через отверстие тонкой стенки.