6. Уравнение Бернулли для потоков реальной жид-ти в каналах.

Определим среднюю удельную кинетическую энергию в данном сечении с учетом неравномерного распределения скоростей.

Умножим и разделим уравнение на U²_ср

α – коэффициент Карриалиса, коэффициент неравномерности поля скоростей

α – отношение действительной кинетической энергии потока к кинетической энергии с тем же расходом, но имеющим равномерное поле скоростей. Тогда уравнение Бернулли для реальной жидкости:

При равномерном поле скоростей α=1.

Для ламинарного движения в круглой трубе α=2.

7. Гидравлический удар.

Если при движении воды или другой жид-ти резко изменить скорость течения (закрыть кран и т.д.), то в трубопроводе возникает гидравлический кран, высланный изменением давления. Гидравлический удар – разрушение трубопровода. Жуковский изучил московский водопровод, трубы которого разрушались, хотя давление в водопроводе было не значительным.

Гидравлический удар можно рассматривать как частный случай неустановившейся жид-ти. Физическую картину гидравлического удара можно представить следующим образом:

После закрытия резко крана не вся масса жидк-ти прекращает движение мгновенно. Вначале прекращает движение слой жид-ти непосредственно соприкасающийся с задвижкой, затем последовательно прекращает движение слой жид-ти с увеличивающим расстояние от задвижки при этом давление увеличится до уровня превышающего давление в напорном баке. В каждом сечении трубопровода будет возникать колебательный процесс, но вследствие сопротивления колебания будут затухать. При эксплуатации …

Жуковский установил, что

,

где - модуль упругости

, а- скорость звука

β – коэффициент сжимаемости жид-ти

Е зависит от температуры и давления жид-ти.

Зная Е и плотность жид-ти можно определить повышение давления: - формула Жуковского.

Уменьшить ∆p можно за счет медленного закрытия задвижки или крана, за счет использования гидроаккумуляторов.

Лекция 4

1. Закон сопротивления гладких труб.

Закон сопротивления гладких труб впервые был получен экспериментально

- универсальный закон сопротивления для гладких труб при турбулентном течении.

Несколько позднее получена теоретически формула

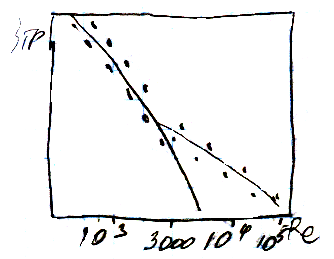
Закон сопротивления соответствующий степенному закону распределения скоростей при n=1/7 был получен в 1811 г Блазиусом

- формула Блазиуса

При Re< 10⁵

В расчетах иногда используют формулу Никуладзе

Иногда используют формулу Кондакова

2. Течение шероховатого

На практике все трубы имеют ту или иную шероховатость. Она характеризуется … степенью гребешков. Называют абсолютной шероховатостью K_S. Рассматривают также относительную K_S/R. При ламинарном течении все шероховатые трубы имеют такое же сопротивление, что и гладкие. При турбулентном режиме рассматривают 3 случая:

1. Без проявления шероховатости, когда сопротивление гладких и шероховатых труб совпадают, т.е. неровности лежат в пределах ламинарного подслоя. Такие трубы называются гидравлически гладкими. ; υ*- динамическая скорость

2. Переходный режим. Он наступает при увеличении числа Re, при уменьшении величины ламинарного подслоя. . Коэффициент трения зависит от Re и от шероховатости.

3. С полным проявлением шероховатости . Коэффициент трения обусловлено не трением, а завихрением, и сопротивление не зависит от Re. Автомодельный режим относительно Re, режим квадратической зависимости гидравлического давления от скорости. . Для шероховатых труб получена интерполяционная формула . Для рактических расчетов используется формула Альтшуля

Прог. скорость шерох.труб менее напол.чем в гладких. Они описываются степенным законом с числом n=