Равенство Маркова

Обозначим через вероятность того, что через шагов (после испытаний) система перейдет из состояния в состояние . Очевидно, что при получим переходные вероятности . По известным переходным вероятностям нужно найти вероятность перехода системы из состояния в состояние через шагов. Для этого введем в рассмотрение промежуточное (между и ) состояние , т.е. будем считать, что из первоначального состояния за шагов система переходит в состояние , с вероятностью , после чего за оставшиеся шагов из промежуточного состояния она перейдет в конечное состояние с вероятностью . По формуле полной вероятности:

.

Полученное выражение называется равенством Маркова.

Если в равенстве Маркова предположить, что , а , то получим:

.

Таким образом, можно найти все вероятности , а значит и матрицу . Далее предположим, что , а , тогда по аналогии с предыдущими рассуждениями, получим .

В общем случае .

Предельные вероятности

Следующей важной задачей является исследование вероятностей переходов системы при неограниченном увеличении числа .

Теорема Маркова. Пусть существует такое число шагов, при которых все вероятности строго положительны (отличны от нуля). Тогда для каждого состояния существует предельная вероятность его наступления, т.е. такое число , что независимо от исходного состояния имеет место равенство .

Смысл содержащегося в теореме утверждения интуитивно понятен: вероятность того, что система окажется в состоянии не зависит от предыстории системы и мало отличается от предельной величины . Найти эти вероятности можно следующим образом. Воспользуемся доказанным ранее равенством Маркова 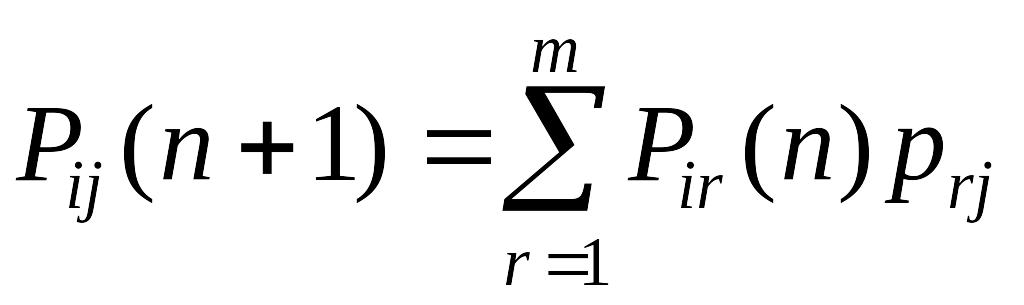. Если перейти к пределу при , то получим . Если дополнить это уравнение условием нормировки , то получится система уравнений, решениями которой и будут искомые величины . Причем, несложно показать, что эта система определяет величины однозначно, т.е. полученные значения единственны.

Контрольные вопросы к теме №2

1. Основные соединения и формулы для их расчета.

2. Правила суммы и произведения.

3. Урновая схема.

4. Понятие схемы независимых испытаний Бернулли.

5. Наивероятнейшее число наступления событий в схеме Бернулли.

6. Теорема Пуассона.

7. Локальная теорема Муавра–Лапласа.

8. Интегральная теорема Муавра–Лапласа.

Тема 3. Случайные величины Лекция 3. Одномерные случайные величины

Основные понятия:

случайная величина; дискретная случайная величина; непрерывная случайная величина; закон распределения; функция распределения; математическое ожидание; дисперсия случайной величины; отклонение случайной величины; среднеквадратическое отклонение; начальный момент порядка ; центральный момент порядка ; закон распределения дискретной случайной величины; биномиальное распределение; распределение Пуассона; геометрическое распределение; функция распределения вероятностей; плотность распределения вероятностей; закон распределения; мода непрерывной случайной величины; медиана непрерывной случайной величины; равномерное распределение; показательное распределение; нормальное распределение; функция Гаусса; теорема Ляпунова; асимметрия распределения случайной величины; эксцесс распределения случайной величины; стандартный интеграл Лапласа; правило «трех сигм»; закон больших чисел; неравенство Чебышева; теорема Чебышева.