Лекция 6. Векторная алгебра
Между духом и материей посредничает математика.
Хуго Штейнхаус
ПЛАН
Введение.
Декартова система координат.
Полярная система координат.
Элементы векторной алгебры.
Скалярное произведение векторов
Заключение.
6.1. Введение
- Дайте мне точку опоры, и я переверну весь мир, – мечтал Архимед в 250 году до нашей эры в Греции.
- Дайте мне универсальный язык, и я опишу весь мир, – мечтал Рено Декарт в1619 году во Франции.
Весь мир для них состоял из предметов и сил, которые приводили эти предметы в движение. Числа и силы, разъединенные физикой и математикой, были мало связаны между собой. Для того чтобы связать их, нужен был новый язык, простой и ясный, который был одинаково понятен всем, кто имеет дело с числами и их изменениями.
Мечта Декарта сбылась. Он нашел универсальный язык, на котором с тех пор говорит весь математический и физический анализ, – язык отвлеченных формул, каждая из которых при внешней похожести может описывать различные явления.
6.2. Декартова система координат
А все началось с оси действительных чисел, на которую Декарт поместил все известные и неизвестные (отрицательные и иррациональные) числа. Каждой точке на этой оси соответствовало свое число. Чем больше абсолютная величина числа – тем дальше находится оно от начала координат. Длина отрезка, заключенного между двумя точками, определяется как разность координат его концевых точек:
.
Определенный таким образом отрезок можно было делить пополам, и координата середины отрезка определялось как среднее его координат, т.е.
.
(6.1)
Если
отрезок АВ
внутренней точкой С
делится в соотношении
,
то координаты точки С
находятся из решения уравнения
,
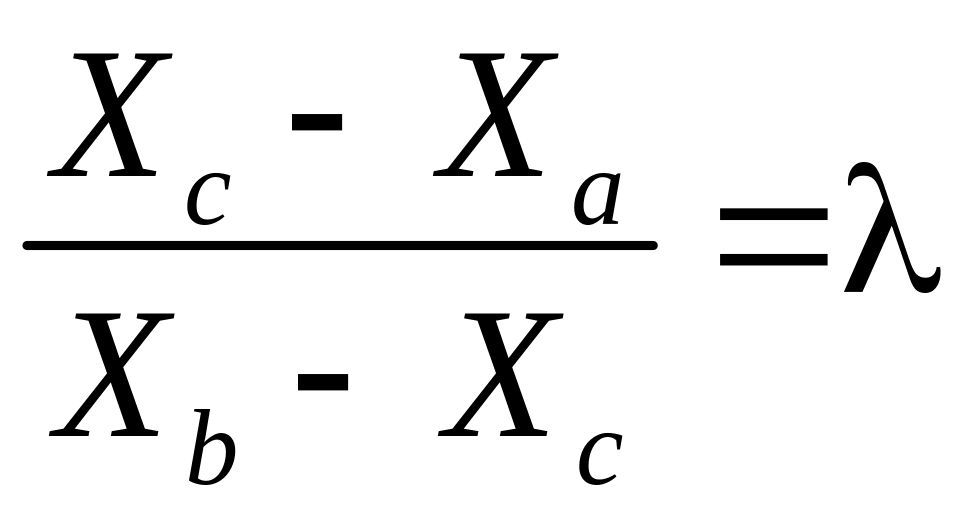откуда
.
(6.2)
Пример 6.1. Найти координаты середины отрезка АВ, если точка А отстоит вправо от начала координат на 5 ед., а точка В – на 13 ед., а также координаты точки K, делящий отрезок в отношении 1:7.
Решение. Воспользуемся выше данными формулами:
,
.
Н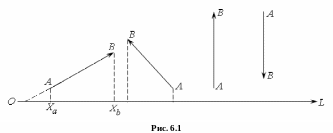
а
эту же ось можно было проецировать силы
– направленные отрезки, которые
назывались векторы.
Векторы обозначаются символами АВ,
,
.
В первых двух случаях начало вектора
находится в точке А,
конец – в точке В,
в третьем случае начало вектора находится
в любой точке (рис. 6.1).
И вновь число, равное разности координат его начала и конца, однозначно характеризовало почти все векторы. Это число называлось проекцией вектора на ось.
(6.3)
Эту формулу вы помните из школы.
По заданной проекции и углу между вектором и положительным направлением оси OL можно было найти модуль вектора или его длину.
,
(6.4)
откуда
.
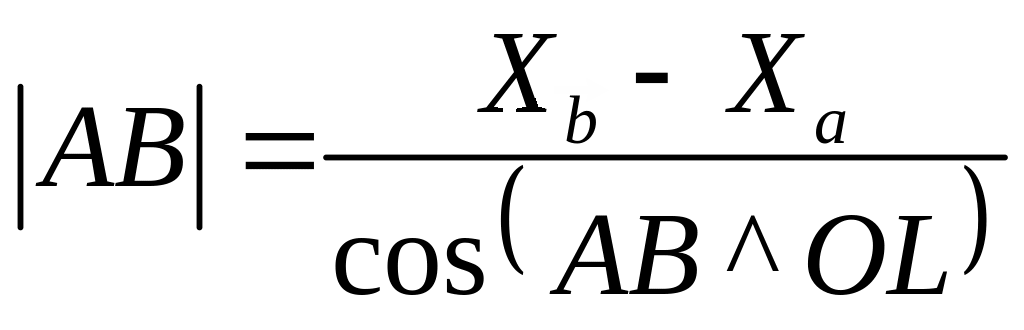Если угол между вектором и осью был острый – проекция считалась положительной, если тупой – отрицательной. Но если вектор был перпендикулярен оси – его проекция становилась равной нулю, и восстановить его модуль было невозможно. Такие векторы либо выпадали из рассмотрения, либо для них нужно было ввести дополнительную ось.
И Декарт ввел ее. Две взаимно перпендикулярные оси, выходящие из одной точки – нуля (начала), как две скрещенные шпаги, разделили плоскость на четыре части. Он назвал их Системой координат, а части квадрантами, или четвертями.
Теперь каждая
точка на плоскости, а потом и в пространстве
могла быть «привязана» к системе. Эти
«привязки» назывались координатами
точки
в декартовой системе координат. Координаты
однозначно определяли положение точки
на плоскости. Например, точка
находится в III
четверти,
,
и т.д.
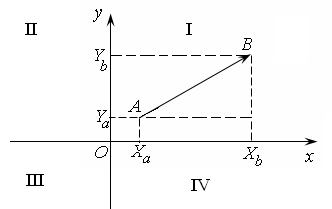
Рис. 6.2. Декартова система координат
Как только точки
получили свои координаты, – сразу стало
возможно определить между ними расстояние.
Если точки А
и В
имели координаты
и
соответственно, то расстояние между
ними определялось по теореме Пифагора
(рис. 6.2). Это была первая формула,
связывающая координаты воедино.
.
(6.5)
Формулы для середины отрезка и для пропорциональных отрезков не изменились, к ним просто добавилась вторая координата:
(6.6)
Формула (6.5) могла определить и модуль вектора (или его длину), если известны координаты начала и конца. В новой системе не было запрета на перпендикулярные векторы, как в случае с одной осью. Перпендикулярные одной, они были параллельны другой, и их модули определялись однозначно. Так родилась новая наука, объектами изучения которой являлись векторы. Она называется векторным анализом. В нашем случае рассмотрение этой темы носит ознакомительный характер. Желающие приобрести более глубокие знания могут обратиться к любому учебнику из списка рекомендованной литературы.