
Лекция 4
Системы линейных уравнений. Основные понятия: совместные и несовместные, определенные и неопределенные системы. Метод Гаусса. Общее решение. Теорема Кронекера-Капелли. Исследование на совместность систем линейных уравнений. Однородные системы и свойства их решений. Фундаментальная система решений.
5. Системы линейных уравнений
5.1. Основные понятия
Рассмотрим произвольную систему линейных уравнений

В общем случае nm.
Решением системы называется такая совокупность n чисел {1,2,...,n}, которая при подстановке в данную систему на место не известных x1,x2,...,xn преобразует все уравнения в тождества. Задача теории систем линейных уравнений состоит в том, чтобы найти все решения системы. При этом возможны три случая.
1) Система вообще не имеет решений. Системы линейных уравнений, не имеющие ни одного решения, называются несовместными. Например, система уравнений

несовместна. С геометрической точки зрения, это соответствует двум параллельным несовпадающим прямым плоскости xOy.
2) Если система, имеющая хотя бы одно решение, называется совместной. Совместные системы могут иметь либо одно решение, либо бесконечно много решений. Системы, имеющие только одно решение, называются определенными. Например,
![]()
С геометрической точки зрения, это соответствует двум пересекающимся прямым плоскости xOy.
3) Система, имеющая бесконечно много решений, называется неопределенной. Например,
![]()
С геометрической точки зрения, это соответствует двум совпадающим прямым плоскости xOy.
Историческая справка. В трактатах до XIX в. рассматривались только квадратные системы линейных уравнений, т.е. системы, у которых число неизвестных равно числу уравнений. В случае несовместных или неопределенных систем довольствовались замечанием о некорректно поставленной задаче. В 1849 г. К. Гаусс (1777-1855) исследовал алгоритм последовательного исключения неизвестных для решения произвольных систем линейных уравнений, который с различными модификациями применяется до сих пор в практических вычислениях. Введение 1877 г. Г. Фробениусом (1849-1897) понятия ранга матрицы, позволило явно выразить условие совместности и определенности систем линейных уравнений через ее коэффициенты (теорема Кронекера-Капелли). Эта теорема содержалась в лекциях, прочитанных Л. Кронекером (1823-1891) в 1883-91 гг. А. Капелли (1858-1892) впервые дал формулировку теоремы с использованием термина "ранг" (1892 г.). К концу XIX в. усилиями К. Вейерштрасса (1815-1897), М. Жордана (1838-1922), Г. Фробениуса, Ш. Эрмита (1822-1901) и др. было завершено построение общей теории систем линейных уравнений.
5.2. Метод Гаусса
Одним из простейших способов решения системы линейных уравнений является прием, основанный на вычислении определителей (правило Крамера). Его преимущество состоит в том, что он позволяет сразу провести запись решения, особенно он удобен в тех случаях, когда коэффициенты системы являются не числами, а какими-то параметрами. Его недостаток – громоздкость вычислений в случае большого числа уравнений, к тому же правило Крамера непосредственно не применимо к системам, у которых число уравнений не совпадает с числом неизвестных. В таких случаях обычно применяют метод Гаусса.
Системы линейных уравнений, имеющие одно и то же множество решений, называются эквивалентными. Очевидно, что множество решений линейной системы не изменится, если какие-либо уравнения поменять местами, или умножить одно из уравнений на какое-либо ненулевое число, или если одно уравнение прибавить к другому.
Метод Гаусса (метод последовательного исключения неизвестных) заключается в том, что с помощью элементарных преобразований система приводится к эквивалентной системе ступенчатого вида. Сначала с помощью 1-го уравнения исключается x1 из всех последующих уравнений системы. Затем с помощью2-го уравнения исключается x2 из 3-го и всех последующих уравнений. Этот процесс, называемый прямым ходом метода Гаусса, продолжается до тех пор, пока в левой части последнего уравнения останется только одно неизвестное xn. После этого производится обратный ход метода Гаусса – решая последнее уравнение, находим xn; после этого, используя это значение, из предпоследнего уравнения вычисляем xn–1 и т.д. Последним находим x1 из первого уравнения.
Преобразования Гаусса удобно проводить, осуществляя преобразования не с самими уравнениями, а с матрицами их коэффициентов. Рассмотрим матрицу:

называемую расширенной матрицей системы, ибо в нее, кроме основной матрицы системы, включен столбец свободных членов. Метод Гаусса основан на приведении основной матрицы системы к треугольному виду (или трапециевидному виду в случае неквадратных систем) при помощи элементарных преобразованиях строк (!) расширенной матрицы системы.
Пример 5.1. Решить систему методом Гаусса:

Решение. Выпишем расширенную матрицу системы и, используя первую строку, после этого будем обнулять остальные элементы:

 получим
нули во 2-й, 3-й и 4-й строках первого
столбца:
получим
нули во 2-й, 3-й и 4-й строках первого
столбца:


Теперь нужно чтобы все элементы во втором столбце ниже 2-й строки были равны нулю. Для этого можно умножить вторую строку на –4/7 и прибавить к 3-й строке. Однако чтобы не иметь дело с дробями, создадим единицу во 2-й строке второго столбца и только
Теперь, чтобы получить треугольную матрицу, нужно обнулить элемент четвертой строки 3-го столбца, для этого можно умножить третью строку на 8/54 и прибавить ее к четвертой. Однако чтобы не иметь дело с дробями поменяем местами 3-ю и 4-ю строки и 3-й и 4-й столбец и только после этого произведем обнуление указанного элемента. Заметим, что при перестановке столбцов меняются местами, соответствующие переменные и об этом нужно помнить; другие элементарные преобразования со столбцами (сложение и умножение на число) производить нельзя!


Последняя упрощенная матрица соответствует системе уравнений, эквивалентной исходной:
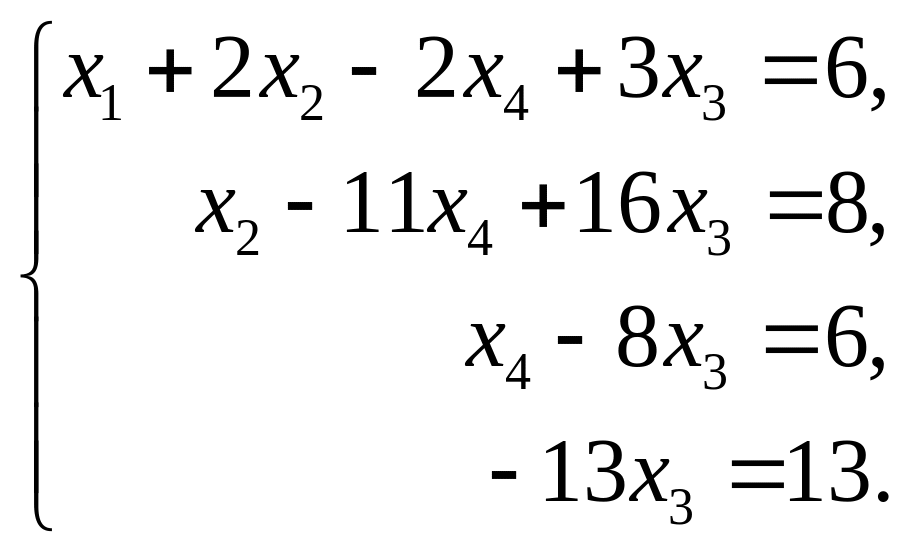
Отсюда, используя обратный ход метода Гаусса, найдем из четвертого уравнения x3 = –1; из третьего x4 = –2, из второго x2 = 2 и из первого уравнения x1 = 1. В матричном виде ответ записывается в виде

Мы рассмотрели случай, когда система является определенной, т.е. когда имеется только одно решение. Посмотрим, что получится, если система несовместна или неопределенна.
Пример 5.2. Исследовать систему методом Гаусса:

Решение. Выписываем и преобразуем расширенную матрицу системы


Записываем упрощенную систему уравнений:

Здесь, в последнем уравнении получилось, что 0=4, т.е. противоречие. Следовательно, система не имеет решения, т.е. она несовместна.
Пример 5.3. Исследовать и решить систему методом Гаусса:

Решение. Выписываем и преобразуем расширенную матрицу системы:


В результате преобразований, в последней строке получились одни нули. Это означает, что число уравнений уменьшилось на единицу:
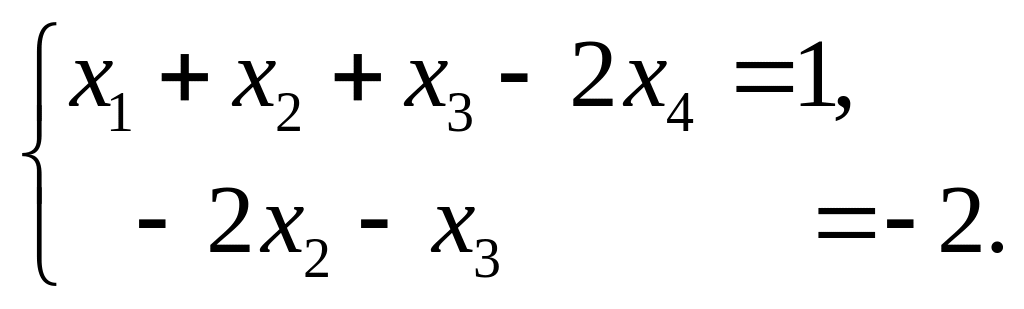
Таким образом, после упрощений осталось два уравнения, а неизвестных четыре, т.е. два неизвестных "лишних". Пусть "лишними", или, как говорят, свободными переменными, будут x3 и x4. Тогда

Полагая x3 = 2a и x4 = b, получим x2 = 1–a и x1 = 2b–a; или в матричном виде

Записанное подобным образом решение называется общим, поскольку, придавая параметрам a и b различные значения, можно описать все возможные решения системы.
