Определители n-го порядка
Чтобы сформулировать определение определителя любого порядка, необходимо ввести понятие минора и алгебраического дополнения матрицы.
Дополнительным минором Mij элемента aij называется определитель, получаемый из данного путем вычеркивания i-й строки и j-го столбца. Алгебраическим дополнением Aij элемента aij называется минор этого элемента, взятого со знаком (–1)i+j, т.е. Aij = (–1)i+jMij.
Например, найдем миноры и алгебраические дополнения элементов a23 и a31 определителя
Получаем
Используя понятие алгебраического дополнения можно дать определение определителя n-го порядка
Определителем n-го порядка называется сумма произведений элементов первой строки на их алгебраические дополнения:
.
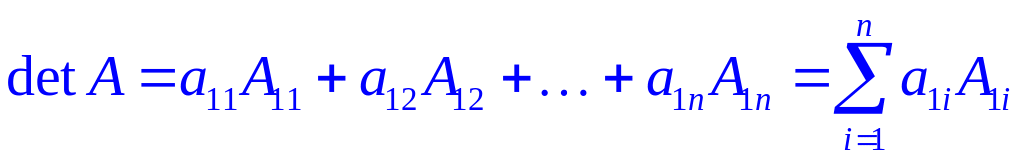(2.11)
Формула (2.11) представляет собой правило составления определителя n-го порядка по элементам первой строки соответствующей ему матрицы и по минорам элементов первой строки, являющиеся определителями (n–1)-го порядка.
Естественно возникает вопрос, нельзя ли использовать для получения величины определителя элементы и отвечающие им алгебраические дополнения не первой, а произвольной i-й строки, и не только строки, но и столбца. Ответ на этот вопрос даёт следующая основная теорема теории определителей (теорема о разложении определителя n-го порядка по строке или столбцу).
Теорема 2.1. Определитель матрицы A равен сумме произведений всех элементов некоторой строки (или столбца) на их алгебраические дополнения:
(2.12)
Доказательство основной теоремы не приводится (см. дополнение 1).
Данная теорема лежит в основе одного из основных методов вычисления определителей, т.н. метода понижения порядка. В результате разложения определителя n-го порядка по какой-либо строке или столбцу, получается n определителей (n–1)-го порядка. Чтобы таких определителей было меньше, целесообразно выбирать ту строку или столбец, в которой больше всего нулей. На практике формулу разложения определителя обычно записывают в виде:
(2.13)
т.е. алгебраические дополнения записывают в явном виде через миноры.
Примеры 2.4. Вычислить определители, предварительно разложив их по какой-либо строке или столбцу. Обычно в таких случаях выбирают такой столбец или строку, в которой больше всего нулей. Выбранную строку или столбец будем обозначать стрелкой.
;
Основные свойства определителей
Разлагая определитель по какой-либо строке или столбцу, мы получим n определителей (n–1)-го порядка. Затем каждый из этих определителей (n–1)-го порядка также можно разложить в сумму определителей (n–2)-го порядка. Продолжая этот процесс, можно дойти до определителей 1-го порядка, т.е. до элементов матрицы, определитель которой вычисляется. Так, для вычисления определителей 2-го порядка придется вычислить сумму двух слагаемых, для определителей 3-го порядка – сумму 6 слагаемых, для определителей 4-го порядка – 24 слагаемых. Число слагаемых будет резко возрастать по мере увеличения порядка определителя. Это означает, что вычисление определителей очень высоких порядков становится довольно трудоемкой задачей, непосильной даже для ЭВМ. Однако вычислять определители можно и по-другому, используя свойства определителей.
Свойство 1. Определитель не изменится, если в нем поменять местами строки и столбцы, т.е. при транспонировании матрицы:
.
Доказательство см. дополнение 1.
Данное свойство свидетельствует о равноправии строк и столбцов определителя. Иначе говоря, любое утверждение о столбцах определителя справедливо и для его строк и наоборот.
Свойство 2. Определитель меняет знак при перестановке двух строк (столбцов).
Предположим вначале, что переставлены две соседние строки матрицы: i и i+1. Разложим определитель исходной матрицы по элементам i-й строки, а определитель новой матрицы (с переставленными строками) ' – по элементам (i+1)-й строки. Разложения будут отличаться только знаком, т.к. в формуле (2.7) для ' каждое алгебраическое дополнение будет иметь противоположный знак – множитель (–1)i+j сменится на множитель –(–1)i+1+j, поэтому '=–.
Если переставить не соседние строки, а скажем i-ю и (i+k)-ю, то такую перестановку можно представить как последовательное смещение i-й строки на k строк вниз, а (при этом каждый раз знак определителя меняется), а (i+k)-й строки на (k–1) вверх, что тоже сопровождается (k–1) изменением знака, т.е. знак поменяется нечётное число (2k–1) раз: '=–.
Свойство 3. Общий множитель всех элементов в какой-либо строке (столбце) можно вынести за знак определителя.
Например,
Для доказательства этого утверждения достаточно разложить по первой строке определитель, стоящий слева.
Рассмотренное
свойство диссонирует со свойствами
умножения матрицы на число. Действительно,
при умножении матрицы на число все её
элементы умножаются на это число – это
лишь умножение одной строки или столбца
матрицы определителя на это число.
Поэтому, если A
– квадратная матрица порядка n,
то
.
Свойство 4. Если все элементы i-й строки (j-го столбца) определителя представлены в виде суммы двух слагаемых, то и весь определитель представляется в виде суммы двух определителей, у которых все строки (столбцы) за исключением i-й (j-го), такие же, как и в исходном определителе, а i-я строка (j-й столбец) в первом определителе состоит из первых слагаемых и во втором – из вторых.
Например,
Для доказательства этого утверждения достаточно разложить по второй строке определитель, стоящий слева.
Свойство 5. Определитель не изменится, если к элементам одной строки (столбца), прибавить элементы другой строки (столбца), умноженной на какое-либо число.
Например,
Для доказательства этого равенства достаточно разложить определитель по второй строке, разбить на две группы слагаемых и собрать их снова в виде двух определителей:
.
Поскольку второй определитель равен нулю, то видим, что определитель не меняется.
Свойство 6. Определитель произведения матриц равен произведению определителей матриц:
.
Доказательство этого свойства не приводится (см. дополнение 1).
Теорема 2.2. Определитель равен нулю, если он имеет:
1) хотя бы две одинаковые строки (столбца);
2) нулевую строку (столбец);
3) хотя бы две строки (столбца), элементы которых пропорциональны;
4) хотя бы одну строку (столбец), являющуюся линейной комбинацией других строк (столбцов).
1) Действительно переставим эти две строки (столбца). С одной стороны определитель не изменится, а с другой, по свойству 2, поменяет знак, т.е. =–, откуда =0.
2) Это утверждение вытекает из свойства 3 при k=0.
3) Действительно вынося коэффициент пропорциональности за знак определителя, получим определитель с двумя одинаковыми строками (столбцами); отсюда следует, что он равен нулю.
4) здесь достаточно использовать свойства 3 и 4.