Дополнение 3 к главе 2. Определение определителя через его элементы

При изучении определителей второго и третьего порядков можно было заметить, что всякий член определителя является произведением элементов, взятых по одному в каждой строке и в каждом столбце. Такой подход к определению определителя можно сохранить и при рассмотрении определителя n-го порядка.

Пусть теперь дана квадратная матрица

. (2.25)

Рассмотрим всевозможные произведения по n элементов этой матрицы, расположенных в разных строках и разных столбцах, т.е. произведения вида

, (2.26)

где индексы ₁, ₂, …, _n составляют некоторую перестановку из чисел 1, 2, …, n. Число таких произведений равно числу различных перестановок из n элементов, т.е. равно n!

Для определения знака, с каким произведение (2.2) входит в состав определителя, заметим, что из индексов этого произведения можно составить подстановку

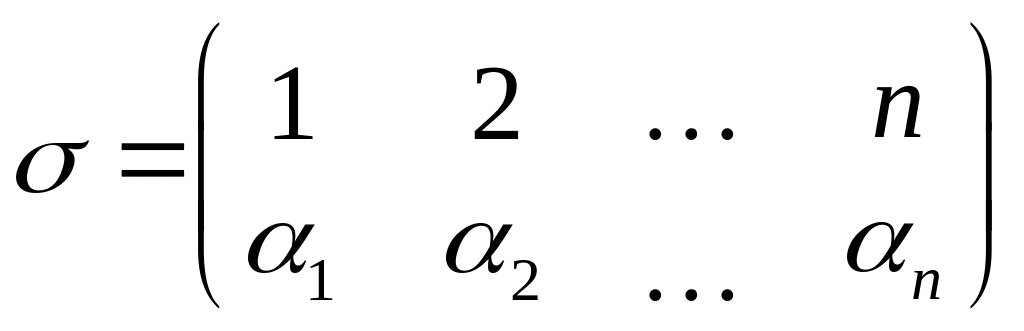, (2.27)

где i переходит в _i, если в состав произведения (2.26) входит элемент, стоящий в i-й строке и в _i-м столбце матрицы (2.25). Рассматривая выражения определителей второго и третьего порядков, можно заметить, что в них со знаком плюс входят те члены, индексы которых составляю чётную подстановку, а со знаком минус – члены с нечёткой подстановкой индексов. Естественно сохранить эту закономерность и в определении определителя n-го порядка.

Таким образом, мы приходим к следующему определению.

Определителем n-го порядка, соответствующим матрице (2.25), называется алгебраическая сумма n! членов, составленная следующим образом: членами служат всевозможные произведения n элементов матрицы, взятых по одному из каждой строки и из каждого столбца, причём член берётся со знаком плюс, если его индексы составляют чётную подстановку, и со знаком минус – в противоположном случае.

Кратко это можно записать так:

. (2.28)

Здесь сумма берётся по всевозможным подстановкам (2.27) и .

Приведённое определение определителя даёт в частных случаях n=2 и n=3 те же формулы. Например, при n=2 из элементов матрицы

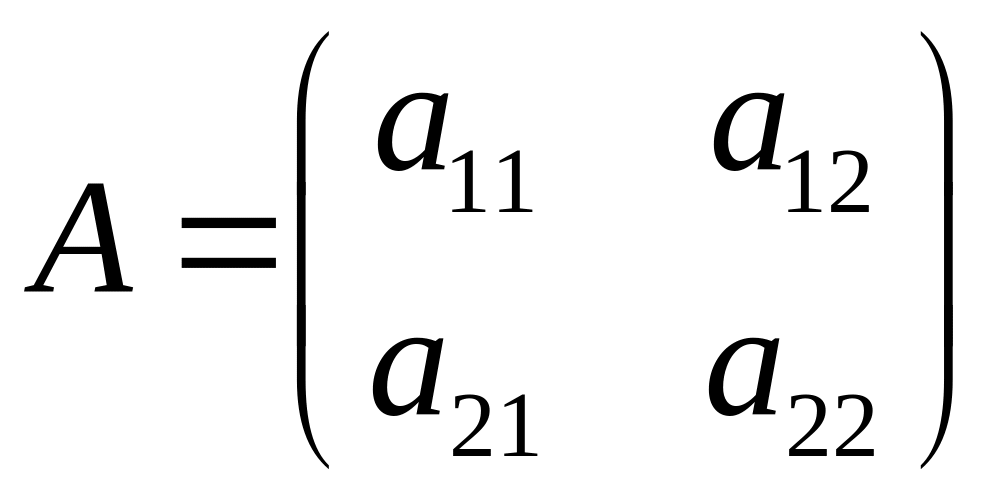
можно составить только два указанных в определении произведения a₁₁a₂₂ и a₁₂a₂₁, которым соответствуют подстановки

и ,

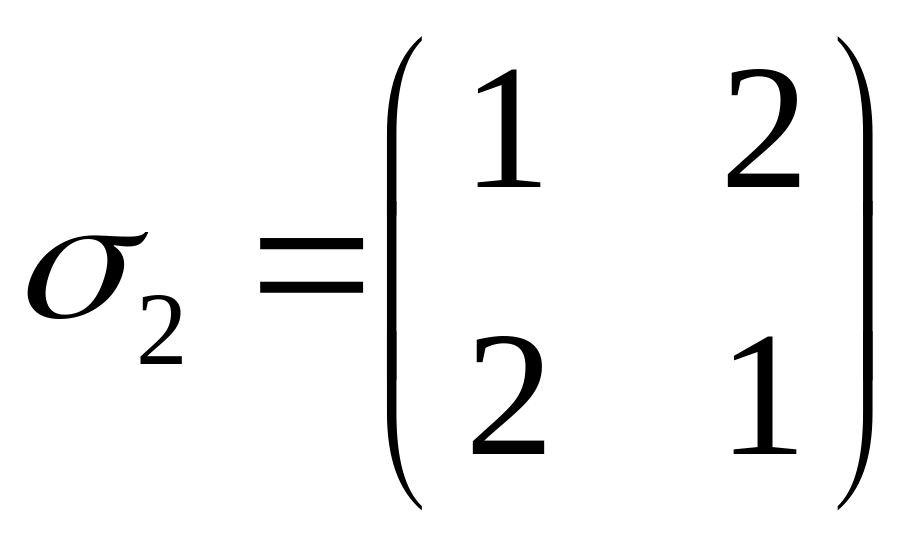чётная и нечётная соответственно, т.к. |₁|=0, а |₂|=1. Поэтому, согласно формуле (2.28)

Пример 2.18. Найти, чему равен определитель:

Решение. Согласно определению  есть алгебраическая сумма 4!=24 слагаемых, но здесь только одно слагаемое a₁₄a₂₃a₃₂a₄₁ отлично от нуля. Ему соответствует подстановка

.

Число инверсий в этой подстановке равно ||=6. Следовательно, слагаемое a₁₄a₂₃a₃₂a₄₁ надо взять со знаком плюс. В результате получаем, что

. 

Пример 2.19. Найти, при каких значениях i и j член a₅₁a_1ia_2ja₄₃a₃₂ определителя пятого порядка имеет знак минус.

Решение. Индексы i и j могут принимать только следующие значения: а) i=4, j=5 или б) i=5, j=4, т.к. при других значениях i и j произведение a₅₁a_1ia_2ja₄₃a₃₂ будет содержать по меньшей мере два элемента из одного столбца. Расположим элементы в порядке возрастания первых индексов: a_1ia_2ja₃₂a₄₃a₅₁. Этому члену соответствует подстановка

.

Пусть а) i=4, j=5. Тогда получим подстановку

,

число инверсий которой равно |=8. Следовательно, при i=4, j=5 данное слагаемое берётся со знаком плюс.

Пусть б) i=5, j=4. Тогда

и |=9. Следовательно, в этом случае данное слагаемое берётся со знаком минус. 