Упражнения и задачи
1.
Выполнить следующие действия:
а)
 ;
б)
;
б)
 .
.
2.
Решить уравнение
 ,
где
,
где
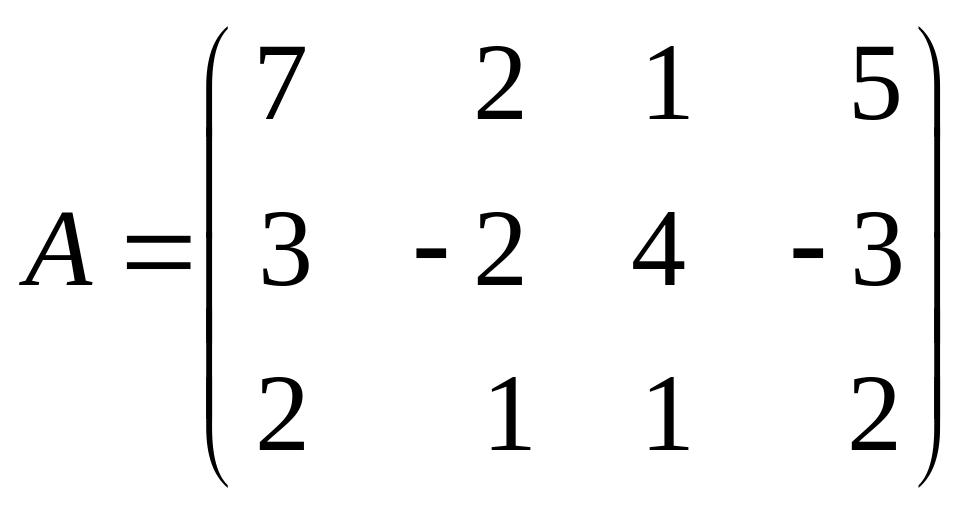 ;
;
 .
.
3.
Найти произведение матриц:
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
;
г)
 ;
д)
;
д)
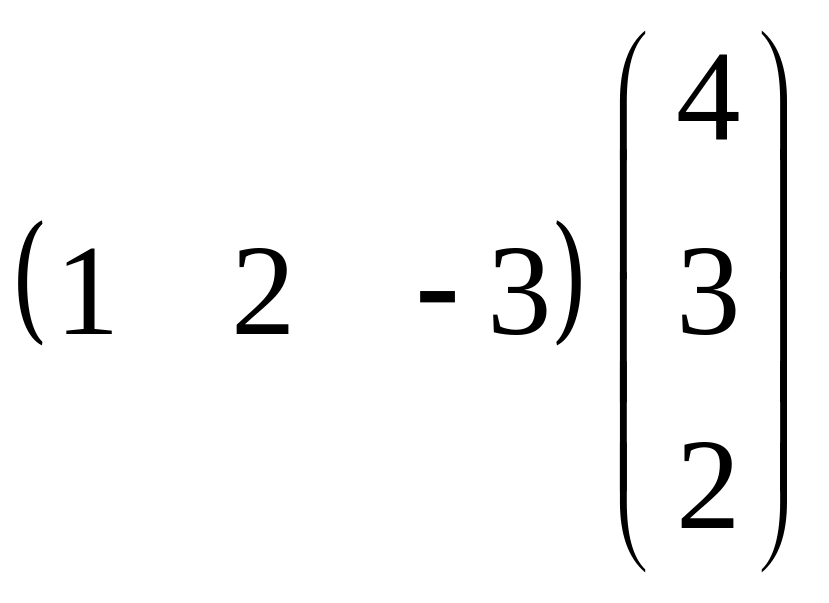 ;
е)
;
е)
 .
.
4.
Найти произведение матриц и проверить
ассоциативный закон умножения:
а)
 ;
б)
;
б)
 .
.
5.
Найти [A,B]=AB–BA
(коммутатор),
если:
а)
 ;
б)
;
б)
 .
.
6.
Найти
(произведение
Йордана),
если:
а)
 ;
б)
;
б)
 .
.
7.
Найти все матрицы, перестановочные с
данной:
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
8.
Найти AAT
и ATA,
если:
а)
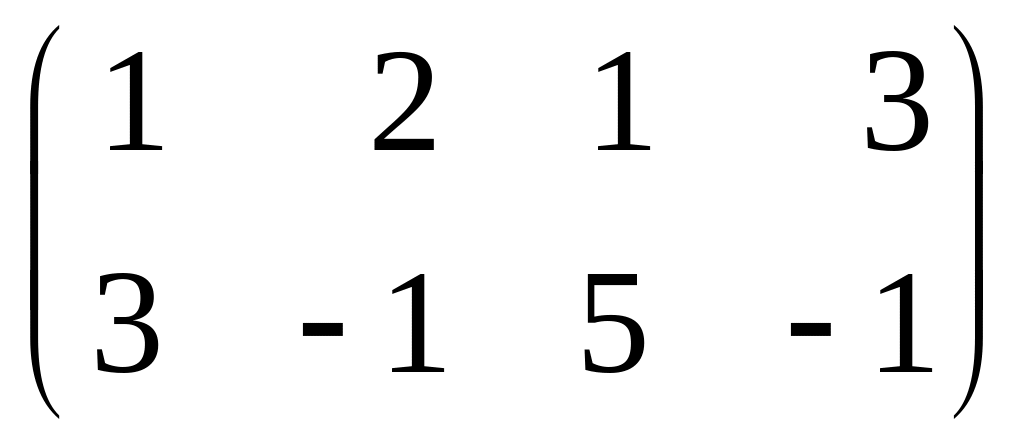 ;
б)
;
б)
 .
.
9.
Проверьте равенство
,
если
 ,
,
 .
.
10.
разложить матрицу A
в сумму симметрической и кососимметрической
матриц, если:
а)
 ;
б)
;
б)
 .
.
11.
Найти:
а)
 ;
б)
;
б)
 ,
в)
,
в)
 ,
г)
,
г)
 .
.
12.
Покажите, что матрица
 – идемпотентная,
– идемпотентная,
 – инволютивная.
– инволютивная.
13.
Найти все матрицы второго порядка,
квадраты которых равны: а) нулевой
матрице; б) единичной матрице.
14.
Найти функции от матриц, если:
а)
 ;
б)
;
б)
 .
.
1
При этом блочные элементы
 сами вычисляются по правилу умножения
матрицы
сами вычисляются по правилу умножения
матрицы
 на число .
на число .


 ;
б)
;
б)
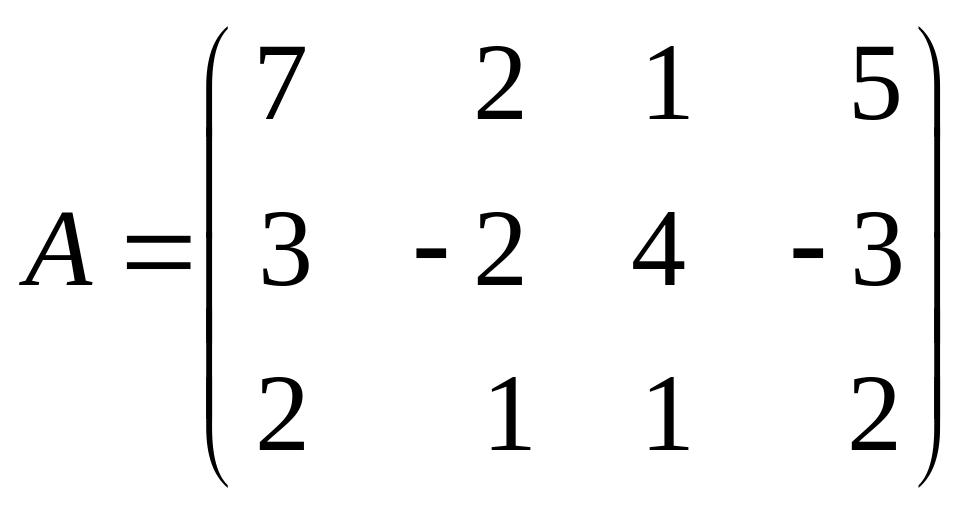 ;
;
 .
. ;
в)
;
в)
 ;
; ;
д)
;
д)
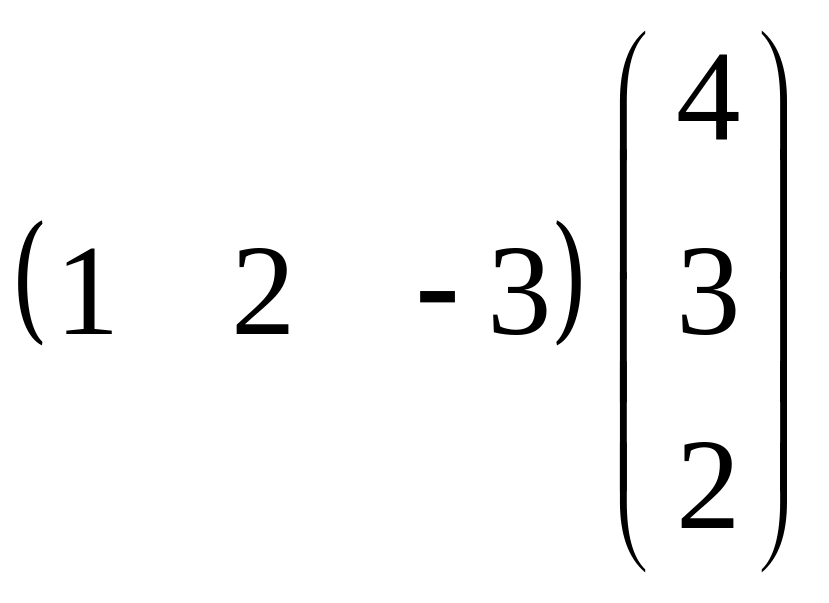 ;
е)
;
е)
 .
. .
. .
. .
. .
. .
. .
. ;
б)
;
б)
 ,
в)
,
в)
 ,
г)
,
г)
 .
. – идемпотентная,
– идемпотентная,
 – инволютивная.
– инволютивная. .
.