*Блочные матрицы
Если
разделить некоторую матрицу A
на части вертикальными и горизонтальными
прямыми, то получаются прямоугольные
ячейки, являющиеся сами по себе матрицами.
Эти ячейки называют блоками
(или клетками)
матрицы. Сама матрица может рассматриваться
как таблица, элементами которой являются
более мелкие матрицы
:
.
При таком построении матрица A
составляется из блоков, и поэтому её
называют блочной
(или клеточной).
Одна и та же матрица может быть разбита на блоки различными способами. Например, рассмотрим матрицу
.
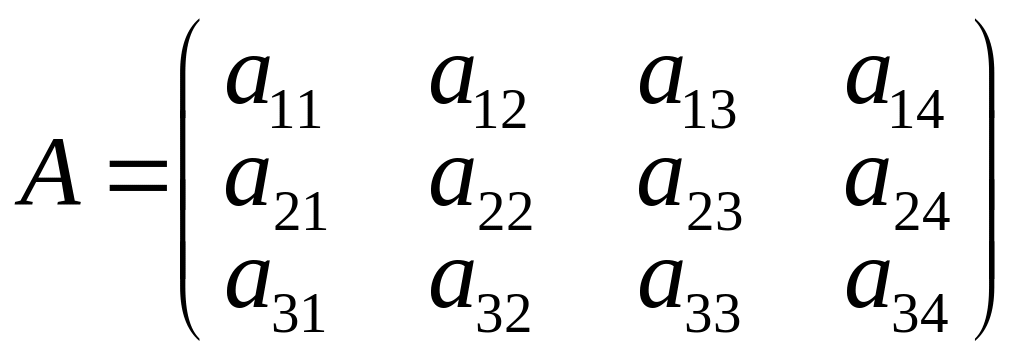Разобьём её на блоки
,
или
,
где
-
,
,
,
.
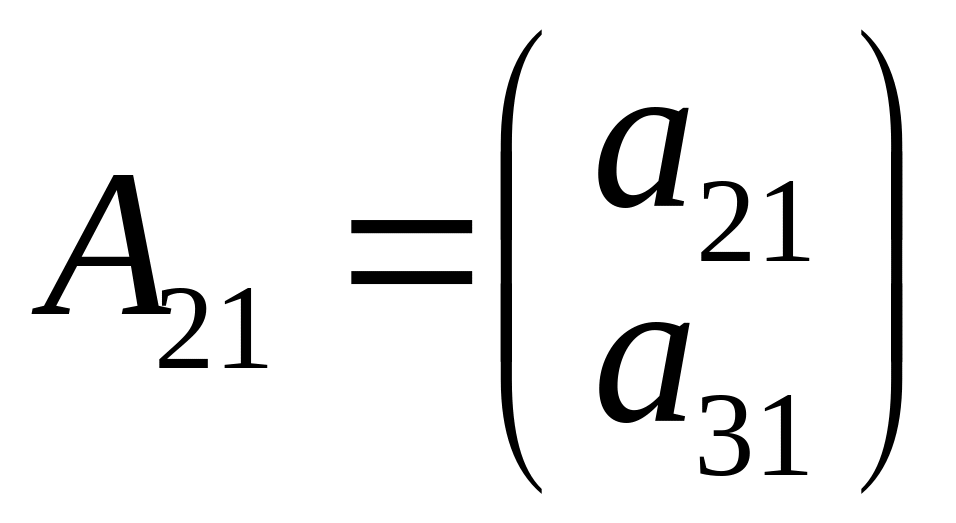Разбивая матрицу иначе, получим
,
или
,
где
|
|
|
|
|
|
,
,
,
,
,
.Блочные матрицы удобны тем, что действия над ними производятся формально по тем же правилам, что и над обычными матрицами. В самом деле, это в достаточной степени очевидно для сложения матриц и умножения матрицы на число.
В
самом деле, элементарно проверяется,
что если матрица
является блочной и имеет блочные элементы
,
то при том же разбиении на блоки матрице
отвечают блочные элементы
1.
Столь
же элементарно проверяется, что если
матрицы A
и B
имеют одинаковые порядки и одинаковым
образом разбиты на блоки, то сумме матриц
A
и B
отвечает блочная матрица с элементами
(здесь
и
– элементы матриц A
и B).
Подробнее
рассмотрим ситуацию с умножением
блочных матриц.
Пусть блочные матрицы
и
удовлетворяют двум условиям.
10. Число «блочных» столбцов матрицы A совпадают с числом «блочных» строк матрицы B (т.е. индекс для A и B изменяется в одинаковых пределах).
20. Для любых индексов , , число столбцов у матрицы A совпадает с число строк у матрицы B.
Тогда
.
Для доказательства этого равенства достаточно расписать обе его части через элементы матриц.
Действительно, рассмотрим две блочные матрицы
,
,
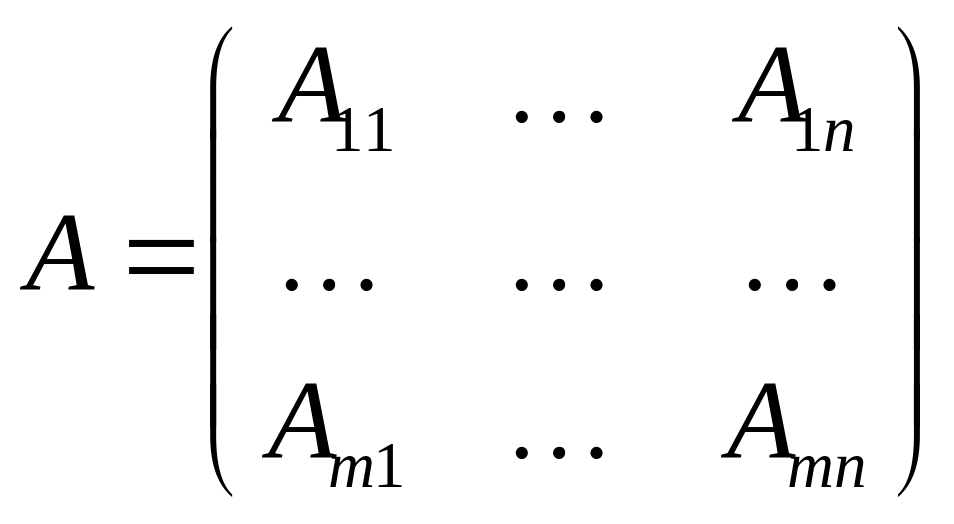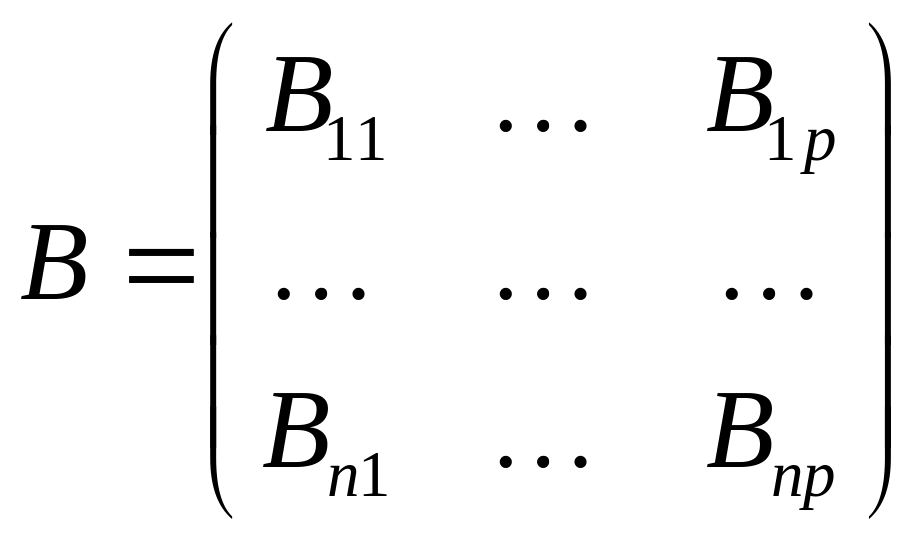Разбитые
на блоки
,
таким образом, что число столбцов блока
равняется числу строк блока
(=1,…,m;
=1,…,n;
=1,…,p).
При этом условии выражения
(1.6)
имеют смысл. Можно показать, что
,
(1.7)
т.е. что матрицы, разбитые надлежащим образом на блоки, можно перемножать обычным путём: блоки произведения равны суммам произведений блоков строк A на блоки соответственных столбцов B.
Докажем сначала это правило в следующем частном случае:
.
(1.8)
Пусть
,
,
,
– элементы соответственных матриц A,
B,
C,
D
(i=1,…,m;
j=1,…,n;
k=1,…,s;
l=1,…,t).
Выполняя действия, указанные в левой
части равенства (1.8), получим, что элемент,
стоящий в i-й
строке и j-м
столбце, будет равен
.
Однако, вычисляя соответственный элемент правой части, получим то же выражение, и, таким образом, равенство (1.8) доказано.
Пользуясь формулой (1.8), теперь можно доказать более общую формулу:
,
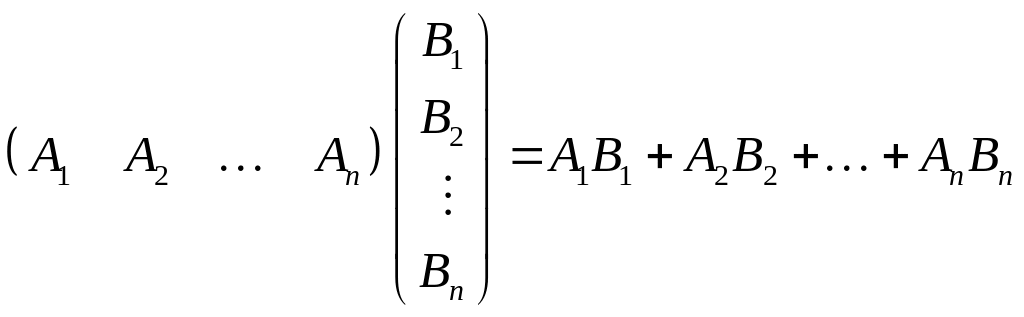(1.9)
где Ai, Bi – отдельные блоки. При n=2 эта формула совпадает с (1.8). Далее применяем метод математической индукции. Пусть для значений n, меньших заданного, формула (1.9) уже доказана, и пусть
.
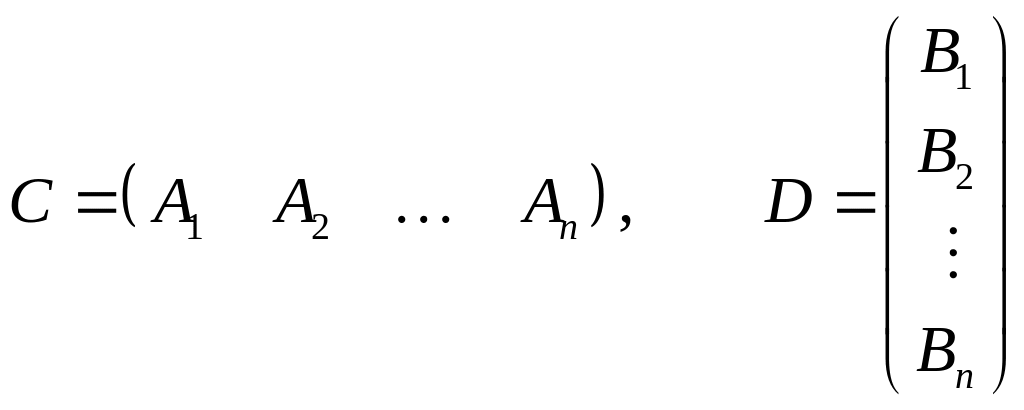Тогда из (1.8) имеем
.
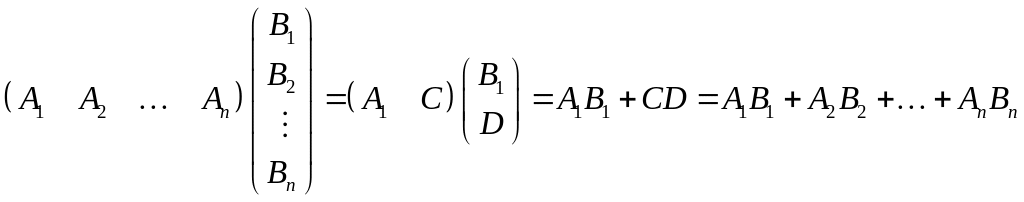Аналогичным путём получаются формулы
,
(1.10)
.
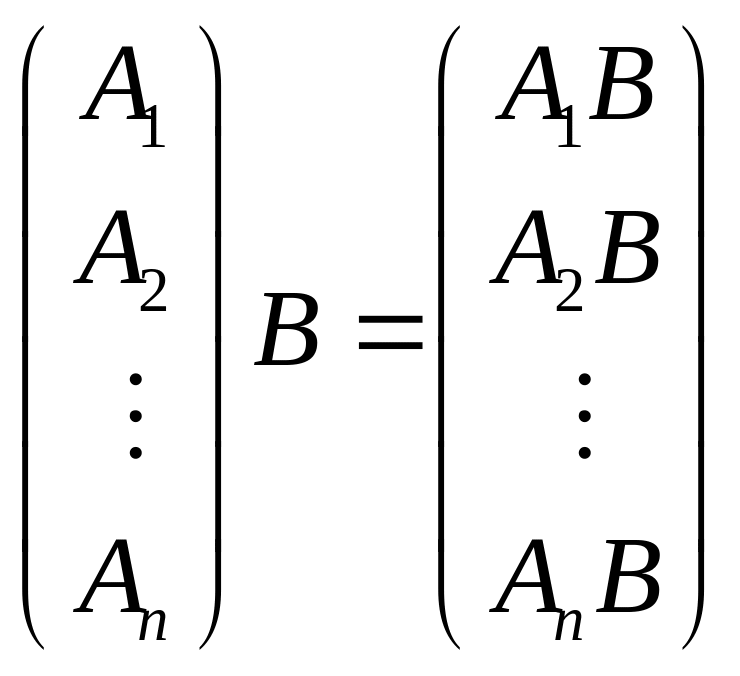(1.11)
Чтобы теперь из частных формул (1.9), (1.10), (1.11) вывести общую формулу (1.7), обозначим строки блоков матрицы A через U1,…, Um, столбцы блоков матрицы V через V1,…, Vp. На основании формулы (1.11)
.
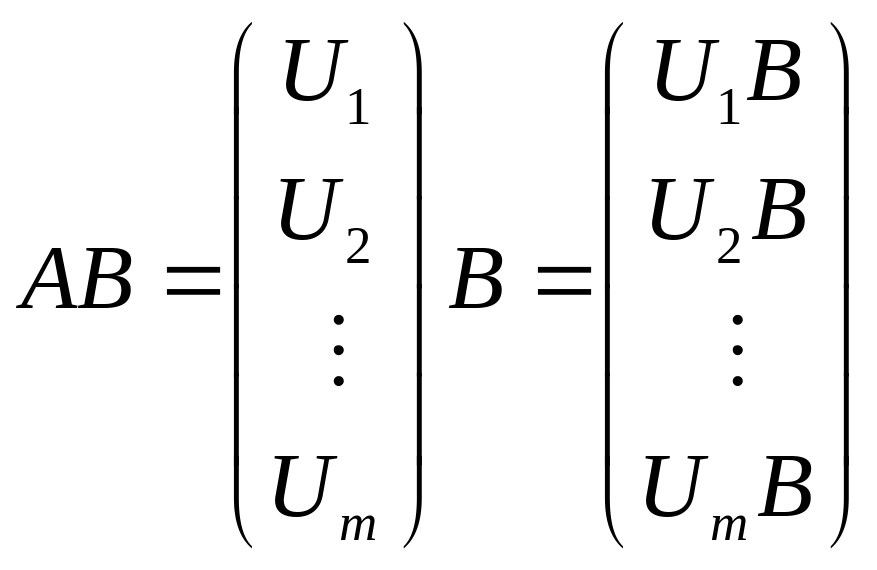Подставляя
сюда вместо матрицы B
её разбиение на блоки
и пользуясь формулой (1.11), получим
.
(1.12)
Однако в силу (1.9)
.
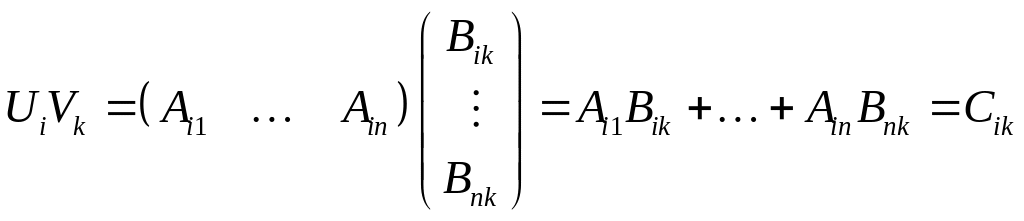Подставляя эти выражения в (1.12), получим формулу (1.7).
Пример 1.6. Перемножить матрицы при указанном подразделении их на блоки:
,
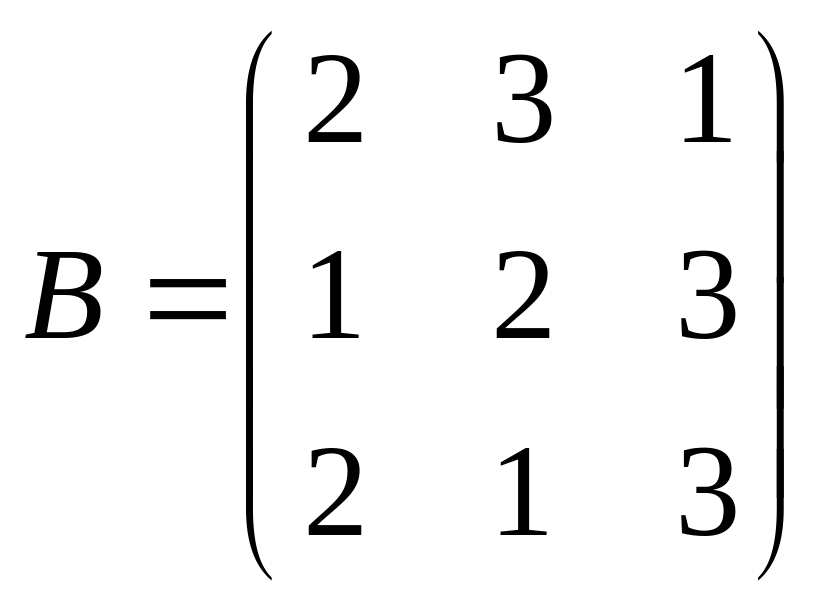
Решение. В данном случае можно написать
,
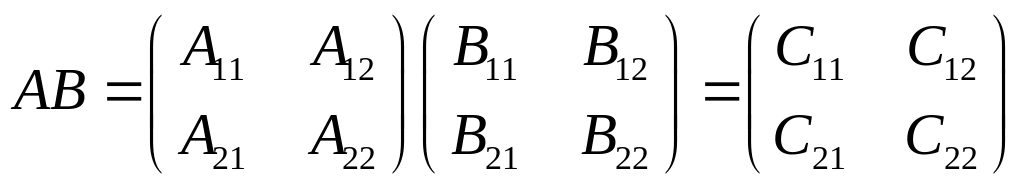где
,
,
,
.
В результате получаем следующую блочную матрицу
.
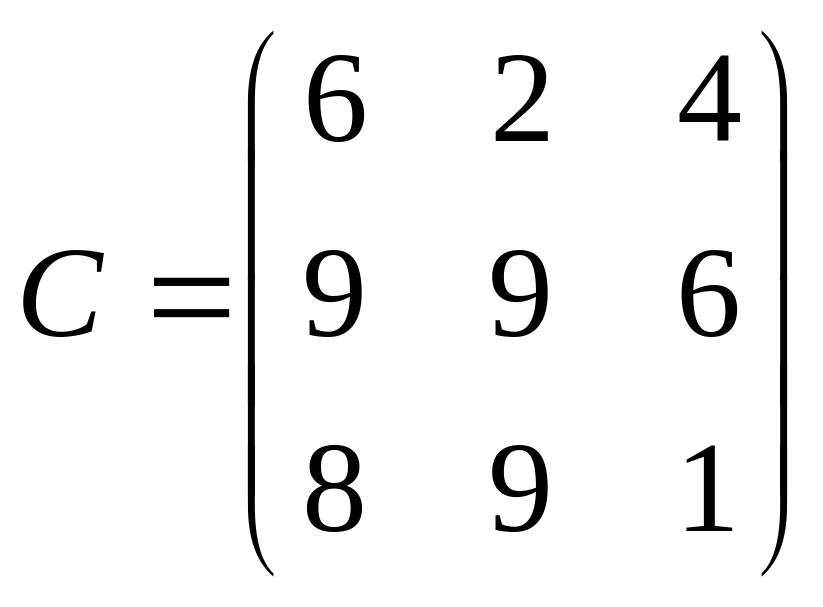
Чаще всего квадратные матрицы разбивают на блоки таким образом, чтобы диагональные блоки (т.е. блоки, расположенные вдоль главной диагонали) были квадратными.
Легко показать, что для выполнения умножения двух блочных матриц достаточно (но, как показывает пример 1.6, не необходимо), чтобы диагональные блоки были квадратными, причём порядки соответствующих диагональных блоков должны быть равны между собой.
Представление матриц в блочном виде часто оказывается удобным при нахождении суммы произведения, если матрицы имеют достаточно большие размеры, а их согласованные разбиения на блоки содержат нулевые, единичные, диагональные, треугольные матрицы.
Пример 1.7. Найдём произведения следующих блочных матриц предполагая, что все операции определены:
,
,
.
Блочная матрица вида
,
где A1, A2, …, As – квадратные матрицы, а O – нулевые матрицы надлежащих размерностей, называется блочно-диагональной (или квазидиагональной). Иногда квазидиагональную матрицу называют распавшейся матрицей.
Прямой суммой двух квадратных матриц A и B порядков m и n соответственно называется квадратная блочная матриц C порядка m+n, равная
.
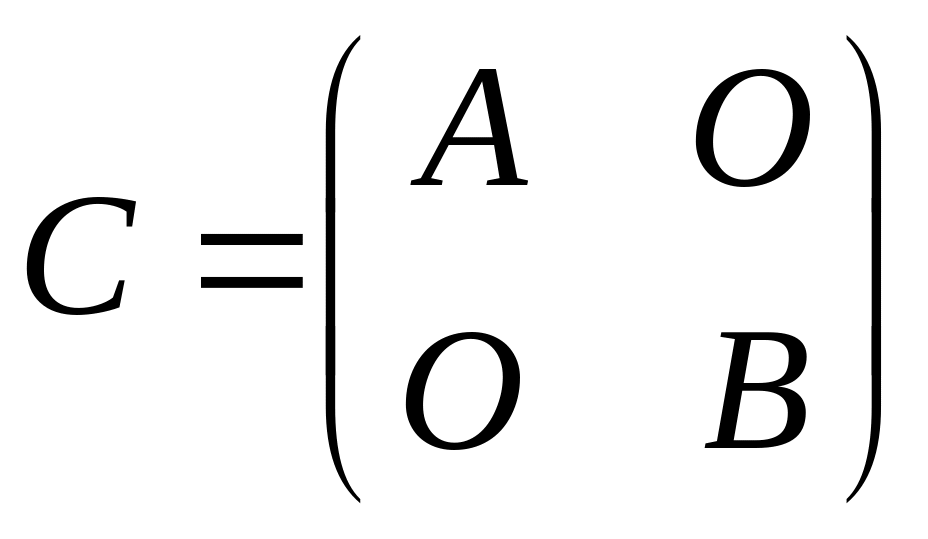Для обозначения прямой суммы матриц A и B используется запись C=AB.
Из определения прямой суммы матриц A и B очевидно, что эта сумма, вообще говоря, не обладает перестановочным свойством.
Укажем основные свойства прямой суммы матриц.
10.
Ассоциативность:
.
В результате выполнения операций в левой и правой частях равенства получается одна и та же блочно-диагональная матрица
,
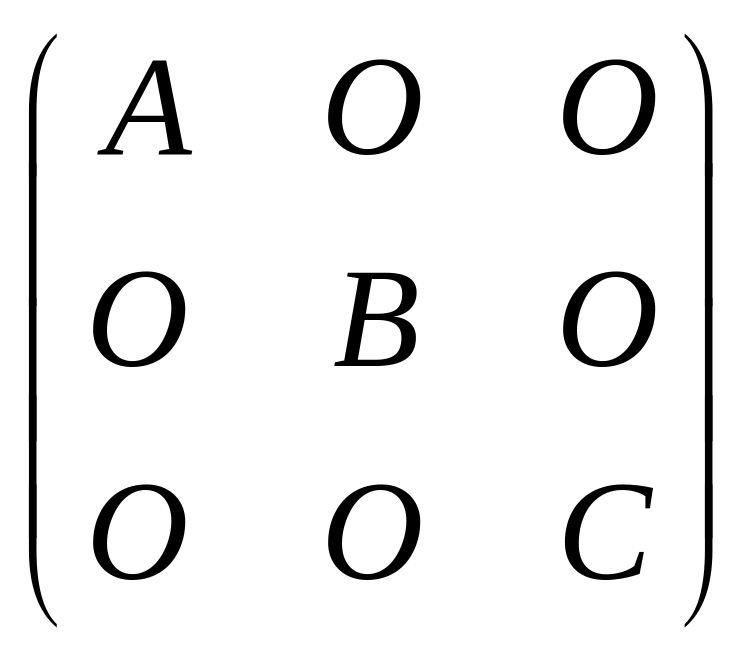где нулевые матрицы имеют соответствующий вид.
20. Пусть квадратные матрицы A1 и A2 имеют порядок m, а квадратные матрицы B1 и B2 – порядок n. Тогда
,
.
Действительно, эти записи означают следующее:
,
,
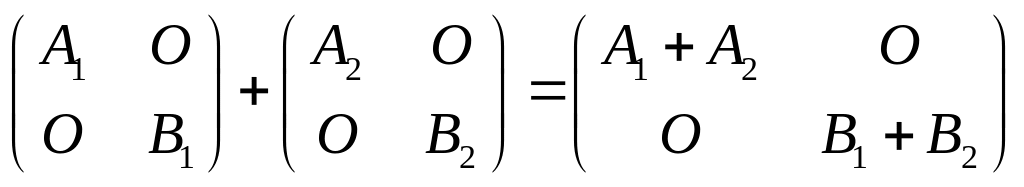что соответствует опепациям над блочными матрицами.
Отметим, что некоторые вычисления, связанные с системами линейных уравнений, значительно сокращаются, если использовать понятие кронекерова произведения матриц.
Пусть A и B – прямоугольные матрицы с размерами mn и pq соответственно. Кронекеровым (или прямым) матриц A и B называется mpnq-матрица C, которую в блочном виде можно изобразить так:
.
Для обозначения кронекерова произведения матриц A и B используется запись C=AB.
Для кронекерова произведения матриц выполнены свойства:
а)
;
б)
;
в)
;
г)
;
д)
;
е)
.