101. Действующее, амплитудное и среднее значение несинусоидальных токов и напряжений.

Под действующим значением тока (напряжения, ЭДС) понимают его среднее квадратичное значение за период:

.

При наличии аналитического выражения функции и возможности взятия интеграла от ее квадрата действующее значение определяется точно. Однако в общем случае на практике действующее значение переменной определяется на основе информации о действующих значениях конечного ряда гармонических.

Мгновенное значение тока – сумма разложенных гармоник и постоянной составляющей.

Пусть ток:

,

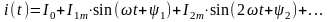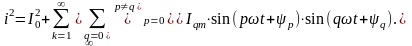
Так как:

и

,

то получаем:

.

При нахождении действующего значения тока необходимо вычислить ток каждой гармоники, используя .

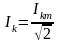В итоге: следовательно действующее значение тока равно корню квадратному из суммы квадратов постоянной составляющей тока и действующих значений отдельных гармоник.

Аналогичные выражения имеют место для действующего значения напряжения, ЭДС.

Среднее значение несинусоидального тока (напряжения, ЭДС) определяется по следующим выражениям:

-среднее по модулю значение: ,

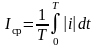-среднее значение за период - (постоянная составляющая): .

102.Коэффициенты, характеризующие форму кривых при несинусоидальных токах и напряжениях.

Для характеристики несинусоидальных периодических переменных служат следующие коэффициенты:

Коэффициент амплитуды – это отношение максимального значения тока к его действующему значению: .

Коэффициент формы – это отношение действующего значения тока к его среднему по модулю значению: .

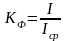Коэффициент искажений – это отношение действующего значения тока первой (основной) гармоники к действующему значению тока: .

Коэффициент гармоник – это отношение действующего значения высших гармонических токов к действующему значению тока первой гармоники (основной): .

Данные расчетные выражения аналогичны и для напряжений и ЭДС.

Вопрос №103.

Активная и реактивная мощности несинусоидального тока. Мощность искажения. Коэффициент искажения.

Под активной мощностью несинусоидального тока понимают среднее значение мгновенной мощности за период первой гармоники: .

В связи с присутствием гармонических составляющих необходимо учитывать мощность от каждой гармоники: , т.е. .

Аналогично для реактивной мощности:

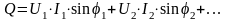, т. е. .

В выражении для реактивной мощности нет постоянной составляющей 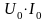, т.к. она присутствует только на активных элементах.

Важно отметить, что (где S – полная мощность), т.к.

.

Здесь вводится понятие мощности искажения Т (не имеет физического смысла), которая определяется:

.

Мощность искажения – мощность определяемая произведениями действующих значений разнопорядковых гармонических тока и напряжения. По величине мощности искажения делают вывод о качестве электрической энергии в электрических сетях.

Отношение 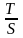показывает степень различия в формах тока и напряжения.

Иной смысл приобретает и коэффициент мощности, который приравнивают к косинусу некоторого условного угл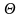а (сдвиг фаз между эквивалентными по действующим значениям синусоидами напряжения и тока): .

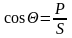Коэффициент искажений – это отношение действующего значения тока первой (основной) гармоники к действующему значению тока: .