96. Расчёт несимметричного режима в 3-х фазной цепи методом симметричных составляющих для случая несимметричного участка с сопротивлением в фазах.
Алгоритм для расчета при несимметрии:
несимметричный участок цепи заменяют источниками напряжения в соответствии с принципом компенсации
неизвестные напряжения на зажимах этих источников раскладывают на симметричные составляющие
применяя метод наложения, разбивают несимметричный режим на три симметричных с источниками соответственно прямой, обратной и нулевой последовательностей. расчет симметричных режимов ведется на одну фазу
применяют теорему об активном двухполюснике и преобразуют однофазные расчетные схемы, заменяя всю симметричную часть эквивалентным двухполюсником и выделяя ветвь несимметричного участка
записывают уравнения по законам Кирхгофа для симметричных составляющих токов и напряжений в преобразованных схемах
составляют дополнительные уравнения, устанавливающие связи между симметричными составляющими токов и напряжений на основе анализа несимметричного участка
определяют симметричные составляющие токов и напряжений как непосредственно на участке несимметрии, так и в любой другой части схемы
искомые токи и напряжения находят на основе метода наложения.
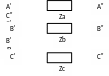
Доп. ур-я, отражающ. вид несимметрии:
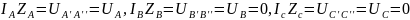
Уравнения для симметричных составляющих:
97. Причины возникновения несинусоидальных периодических токов и напряжений. Свойства и методы расчёта.
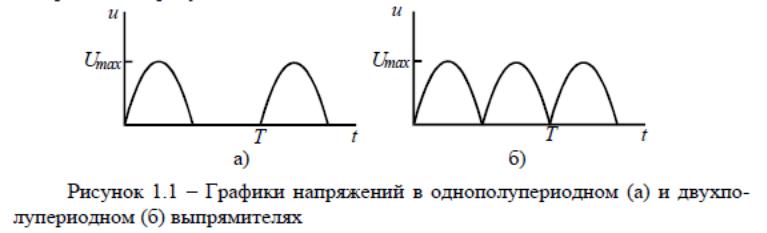
На практике зависимости ЭДС и токов от времени всегда в большей или меньшей степени отличны от синусоидальных. Например, в генераторах пере-менного тока (синхронных генераторах) из – за того, что кривая распределения магнитной индукции вдоль зазора между статором и ротором отличается от си-нусоидальной. Кроме того, в цепях, содержащих нелинейные элементы, даже при синусоидальных ЭДС источников возникают несинусоидальные токи и на-пряжения. К таким цепям можно отнести выпрямители. Графики мгновенных значений напряжения в схемах одно- и двухполупериодного выпрямителей изображены на рисунке 1.1
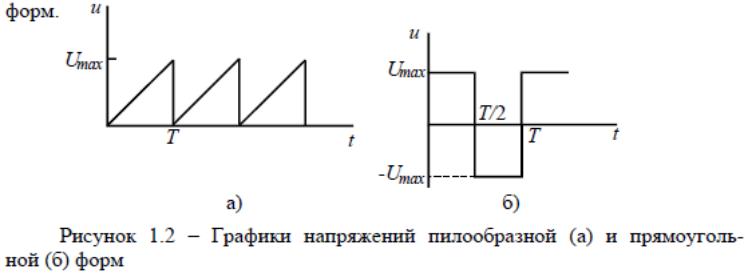
В электронных цепях широкое распространение нашли специальные ге-нераторы несинусоидальных напряжение. Самыми распространенными генера-торами такого типа являются генератор линейно изменяющегося напряжения (ГЛИН) и мультивибратор. Благодаря повторяющимся процессам зарядки и разрядки конденсатора, на выходе генератора возникает соответственно напряжение пилообразной (рисунок 1.2, а) или прямоугольной (рисунок 1.2, б) форм.
Периодическая несинусоидальная функция времени f(t) при любых значениях t удовлетворяет соотношению f(t+T)=f(t), где T - период колебания – наименьшее время, по истечению которого колебания полностью повторяются.
Наиболее наглядным способом представления несинусоидальных величин являются кривые их мгновенных значений (рисунок 1.1 и 1.2), которые можно наблюдать на экране осциллографа. Вторым способом представления периодических несинусоидальных величин является аналитическое разложение функции времени в тригонометрический ряд Фурье.