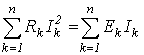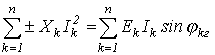- •Источники эдс и источники тока. Реальные и идеальные источники энергии. Их внешние характеристики.
- •Режимы работы источников электрической энергии ( режим холостого хода, короткого замыкания, согласованный, номинальный)
- •Обобщённый закон Ома. Закон Ома для участка цепи
- •Первый и второй законы Кирхгофа. Расчёт электричес-кой цепи по законам Кирхгофа ( на примере электрической цепи).
- •Последовательное, параллельное и смешанное соединение элементов.
- •Метод эквивалентных преобразований с одним источником.
- •Метод контурных токов
- •Метод узловых потенциалов
- •Теорема об активном 2-х полюснике ( принцип эквивалентного генератора)
- •Принцип наложения ( суперпозиции ).
- •Принцип взаимности в линейных электрических цепях.
- •Принцип компенсации.
- •Теорема о взаимных приращениях токов и напряжений ( теорема вариации )
- •Входные и взаимные проводимости. Способы определения.
- •Преобразование звезды в треугольник и треугольника в звезду. Назначение этих преобразований.
- •Эквивалентные преобразования последовательно-параллельных электрических схем с источниками и без источников. Назначение указанных преобразований.
- •Потенциальная диаграмма и её построение
- •Баланс мощности для электрических цепей постоянного и синусоидального токов
- •Основные топологические понятия ( граф, подграф, связный граф, направленно - ориентированный граф, дерево, путь, контур, главный контур, ветви связи ).
- •Передача энергии от активного 2-х полюсника, пассивному.
- •Передача электрической энергии по линии электропередач
- •Топологические матрицы графа и их свойства ( матрица соединений, матрица главных сечений, матрица главных контуров)
- •Первый и второй законы Кирхгофа в матричной форме
- •М етод контурных токов в матричной форме.
- •Метод узловых потенциалов в матричной форме.
- •Основные понятия, относящиеся к переменным и синусоидальным токам (мгновенное и амплитудное значение, период, частота, фаза, начальная фаза). Диапазон частот, применяемый в технике.
- •Способы получения переменных токов. Принцип действия машинного генератора переменного тока.
- •Действующее и среднее значение синусоидально изменяющихся величин.
- •Синусоидальный ток в отдельных элементах электрической цепи.
- •Векторное изображение синусоидально изменяющихся величин
- •Векторная диаграмма. Правила её построения.
- •Комплекс мгновенного значения. Комплексная амплитуда. Комплекс действующего значения.
- •Законы Ома и Кирхгофа в комплексной форме
- •Мощность в цепи синусоидального тока. Активная, реактивная и полная мощности. Единицы их измерения. Треугольник мощностей.
- •Коэффициент мощности. Значение реактивной мощности в электрических сетях. Пути повышения коэффициента мощности.
- •Последовательное соединение r-l-c элементов
- •Резонанс напряжений. Условия возникновения резонанса. Резонансная частота.
- •Колебательный контур. Добротность контура.
- •П араллельное соединение r-l-c элементов. Треугольник токов и проводимостей.
- •Резонанс токов. Условия возникновения резонанса. Резонансная частота.
- •Резонансные кривые.
- •Частотные характеристики.
- •Энергетические процессы при резонансе.
- •Резонанс в сложной цепи
- •45. Магнитосвязанные электрические цепи. Анализ процессов в магнитосвязанных электрических цепях. Коэффициент взаимоиндукции. Коэффициент магнитной связи.
- •Уравнение электрической цепи с взаимной индукцией (на примере электрической цепи ).
- •Последовательное соединение индуктивно-связанных катушек. Согласное и встречное соединение. Сопротивление цепи при согласном и встречном соединении катушек.
- •Параллельное соединение индуктивно-связанных катушек. Согласное и встречное соединение. Сопротивление цепи при согласном и встречном соединении катушек.
- •Воздушный трансформатор ( без ферромагнитного сердечника ). Векторная диаграмма воздушного трансформатора. Коэффициент трансформации.
- •50. Падение и потери напряжения в линии электропередач
- •52. Линейные пассивные четырёхполюсники. Уравнения типа «а». Обобщённые параметры. Связь между коэффициентами.
- •53. Симметричный четырёхполюсник. Связь между коэффициентами.
- •54 Вопрос. Определение коэффициентов четырёхполюсника из опытов холостого хода и короткого замыкания.
- •57. Понятие о мостовых схемах.
- •58. Область применения трёхфазных устройств. Трёхфазный генератор. Принцип действия
- •59.Симметрия, уравновешенность 3-х фазных систем. Практическое значение этих свойств.
- •60. Соединение трёхфазных источников и потребителей в четырёхпроводной и трёхпроводной схемах.
- •61.Получение кругового вращающегося магнитного поля. Асинхронный и синхронный электродвигатели. Принцип действия.
- •62. Соединение 3-х фазной системы звездой. Соотношения между линейными и фазными токами и напряжениями.
- •63. Соединение 3-х фазной системы треугольником. Соотношения между линейными и фазными токами и напряжениями.
Потенциальная диаграмма и её построение
Под потенциальной диаграммой понимают график распределения потенциала вдоль какого-либо участка цепи или замкнутого контура. По оси абсцисс на нем откладывают сопротивления вдоль контура, начиная с какой-либо произвольной точки, по оси ординат - потенциалы. Каждой точке участка цепи или замкнутого контура соответствует своя точка на потенциальной диаграмме.
Рассмотрим последовательность построения потенциальной диаграммы поданным примера 2.
Пример: Построить потенциальную диаграмму для контура abcea (см. рис. 2.9).
Решение. Подсчитаем суммарное сопротивление контура: 4 + 3 + 1 = 8 0м. Выберем масштабы по оси абсцисс (ось х) и по оси ординат (ось у).
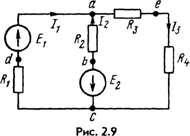
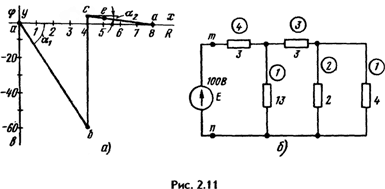
Произвольно примем потенциал одной из точек, например точки a, φa = 0. Эту точку на диаграмме рис. 2.11, а поместим в начало координат.
Потенциал точки b: φb = φa + I24 = φa - 60 = - 60 В; ее координаты: х = 4, у = -60. Потенциал точки с: φc = φb + Е2 = 4 В; ее координаты: х = 4, у = 4. Потенциал точки е: φe = φc + I3R4 = 4 - 1 x 1 = З В; ее координаты: х = 5; у = 3.
Тангенс
угла а1 наклона прямой ааЬ к
оси абсцисс пропорционален току I2,
а тангенс угла а2 наклона
прямой се - току I3; ![]() ,
где mr и mφ - масштабы
по осям х и у.
,
где mr и mφ - масштабы
по осям х и у.
Обратим внимание на различие в знаках, с которыми входит падение напряжения IR при определении потенциала какой-либо точки схемы через потенциал исходной точки и при составлении уравнений по второму закону Кирхгофа. При вычислении потенциала последующей точки через потенциал предыдущей IR берут со знаком минус, если перемещение по сопротивлению R совпадает по направлению с током, тогда как при составлении уравнений по второму закону Кирхгофа IR некоторого участка цепи берут в сумме ΣIR со знаком плюс, если обход этого участка совпадает с направлением тока I на нем.
Баланс мощности для электрических цепей постоянного и синусоидального токов
Баланс мощностей является следствием закона сохранения энергии и может служить критерием правильности расчета электрической цепи.
а) Постоянный ток
Для любой цепи постоянного тока выполняется соотношение:
|
(14) |
Это уравнение представляет собой математическую форму записи баланса мощностей: суммарная мощность, генерируемая источниками электрической энергии, равна суммарной мощности, потребляемой в цепи.
Следует указать, что в левой части (14) слагаемые имеют знак “+”, поскольку активная мощность рассеивается на резисторах. В правой части (14) сумма слагаемых больше нуля, но отдельные члены здесь могут иметь знак “-”, что говорит о том, что соответствующие источники работают в режиме потребителей энергии (например, заряд аккумулятора).
б) Переменный ток. (особенность, полн активная и реактивная состовляющие мощности источника и приемника дБ равны др др)
Из закона сохранения энергии следует, что сумма всех отдаваемых активных мощностей равна сумме всех потребляемых активных мощностей, т.е.
|
(15) |
В ТОЭ доказывается (вследствие достаточной громоздкости вывода это доказательство опустим), что баланс соблюдается и для реактивных мощностей:
|
(16) |
где
знак “+” относится к индуктивным
элементам ![]() ,
,
“-”
– к емкостным ![]() .
.
Умножив
(16) на “j” и сложив полученный результат
с (15), придем к аналитическому выражению
баланса мощностей в цепях синусоидального
тока (без учета взаимной индуктивности):
![]() или
или
![]()