45. Магнитосвязанные электрические цепи. Анализ процессов в магнитосвязанных электрических цепях. Коэффициент взаимоиндукции. Коэффициент магнитной связи.
При протекании тока по катушке возникает ЭДС самоиндукции и потокосцепление самоиндукции, которое будет пронизывать только витки данной катушки.
χ11=W1Ф11=L1i1 χ12=W1Ф12=M12i2
χ22=W2Ф22=L2i2 χ21=W2Ф12=M21i1
M12= M21 – коэффициент взаимоиндукции [Гн]
Определим параметры катушек взаимоиндуктивности при наличии общего потока:
1. полное потокосцепление каждой катушки
χ1= χ11± χ12= W1Ф11± W1Ф12= L1i1± M12i2 χ2= χ22± χ21= W2Ф22± W2Ф21= L2i2± M21i1
«+» ставится, если ток, протекающий по 2ой (1ой) катушке усиливает значение потокосцепления 1ой (2ой) катушки.
«-» если ослабляет.
2. определение ЭДС
е1= -dχ1/dt= -W1* dФ11/dt (-/+) W1* dФ12/dt= -L1*di1/dt (-/+)M12*di2/dt
е2= -dχ2/dt= -W2* dФ22/dt (-/+) W2* dФ21/dt= -L2*di2/dt (-/+) M21*di1/dt
минус ставится при согласном включении, плюс при встречном.
В комплексной форме: Ė1=-jωL1İ1 (-/+) jωM12İ2 ; Ė2=-jωL2İ2 (-/+) jωM21İ1
3. Эдс взаимоиндукции
eM1=± M12*di2/dt ; eM2=± M21*di1/dt
ĖM1=± jωM12İ2 ĖM2=± jωM21İ1
4. Напряжение на катушках
U1= -e1= W1* dФ11/dt ± W1* dФ12/dt= L1*di1/dt ± M12*di2/dt
U2= -e2= W2* dФ22/dt ± W2* dФ21/dt= L2*di2/dt ± M21*di1/dt
5. Сопротивление взаимоиндуктивности
XM=ωМ [Ом]
żM=jωМ [Ом]
6. Коэффициент связи
коэффициент
связи характеризует интенсивность
взаимовлияния 2х катушек при протекании
по ним токов. Не превышает единицу.
Уравнение электрической цепи с взаимной индукцией (на примере электрической цепи ).
Для расчета электрических цепей, имеющих индуктивно связанные катушки используются уравнения Кирхгофа или метод контурных токов.
Теорема об активном двухполюснике может применяться только в том случае, когда выделенная ветвь не имеет индуктивных связей с остальной частью эл.цепи.
Нельзя проводить преобразование треугольника в звезду и звезды в треугольник, если между ветвями есть индуктивная связь.
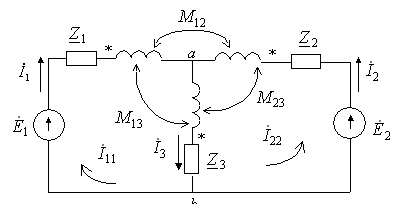
По методу контурных
токов: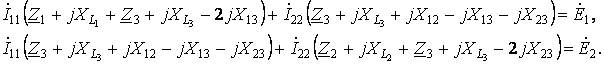
где
.