15. Барометрическая формула. Распределение Больцмана Барометрическая формула — определяет зависимость давления или плотности газа от высоты в поле тяжести

  

Давайте теперь узнаем, откуда же получается барометрическая формула. Давление газа на некой высоте, определяется как :

  

Теперь возьмем колонну в атмосфере и выделим в ней тонкий слой воздуха высотой dh. Ясно, что такой слой вызывает изменение давления на величину dP :

  

Знак минус необходим для того, что с увеличением высоты давление уменьшается

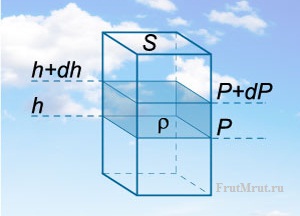
Рассматривая атмосферный воздух как идеальный газ, можно воспользоваться уравнением Менделеева — Клапейрона

  

Из этого уравнения выражаем давление

  

А теперь можно и плотность газа

  

Подставляя найденную плотность газа в дифференциальное уравнение dP, мы получаем :

  

Сделав все преобразования. мы получаем зависимость давления P от высоты подъема h. Теперь необходимо проинтегрировать обе части нашего уравнения:

  

Проинтегрировав, у нас полечилась вот такое уравнение:

  

И теперь последний рывок, это взять логарифм. И у нас получится Барометрическое уравнение.

  

В Формуле мы использовали :

 — Давление газа (атмосферное)

 — Давление газа над уровнем моря

 — Высота над уровнем моря

 — Плотность газа

 — Ускорение свободного падения

 — Постоянная Больцмана

 — Температура

 — Масса одной молекулы

 — Универсальная газовая постоянная

 — Молярная масса

 — Количество вещества

 — Число Авогадро

Распределение Больцмана — концентрация молекул газа под воздействием гравитационного поля в зависити от высоты

  

Из формулы видно, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул (чем меньше высота, тем меньше потенциальная энергия)

Если частицы находятся в состоянии хаотического теплового движения и имеют одинаковую массу и , то распределение Больцмана применимо в любом внешнем потенциальном поле, а не только в поле сил тяжести.

Так же есть формула, показывающая зависимость давления газа от высоты «Барометрическая формула«:

  

В Формуле мы использовали :

 — Концентрация молекул на некой высоте

 — Концентрация молекул на уровне моря

 — Высота над уровнем моря

 — Плотность газа

 — Ускорение свободного падения

 — Постоянная Больцмана

 — Температура

 — Масса одной молекулы

 — Универсальная газовая постоянная

 — Молярная масса

 — Количество вещества

 — Число Авогадро

16. Средняя длина свободного пробега молекул. Среднее число столкновений. Понятие о вакууме.

Молекулы газа, находясь в хаотическом движения, непрерывно сталкиваются друг с другом. Между двумя последовательными столкновениями молекулы проходят некоторый путь l, называемым длиной свободного пробега. В общем случае длина пути между последовательными столкновениями различна, но так как мы имеем дело с очень большим числом молекул и они находятся в беспорядочном движении, то можно говорить о средней длине свободного пробега молекул <l>.  Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d (рис. 1). Он зависит от скорости сталкивающихся молекул, т. е. от температуры газа (несколько уменьшается с ростом температуры). 

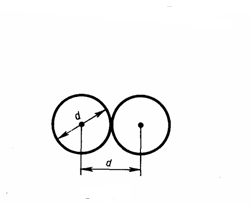
Рис.1

Так как за 1 с молекула в среднем проходит путь, который равен средней арифметической скорости <v>, и если < z > — среднее число столкновений, которые одна молекула газа делает за 1 с, то средняя длина свободного пробега будет    Для определения < z > представим себе молекулу в виде шарика диаметром d, которая движется среди других как бы застывших молекул. Эта молекула столкнется только с теми молекулами, центры которых находятся на расстояниях, равных или меньших d, т. е. лежат внутри так называемого ломаного цилиндра радиусом d (рис. 2).  Среднее число столкновений за 1 с равно числу молекул в объеме, так называемого ломаного цилиндра:    где n — концентрация молекул, V = πd²<v> ,где <v> — средняя скорость молекулы или путь, пройденным ею за 1 с). Таким образом,среднее число столкновений    Расчеты показывают, что при учете движения других молекул    Тогда средняя длина свободного пробега    т. е. <l> обратно пропорциональна концентрации n молекул. С другой стороны, p=nkt. Значит,   

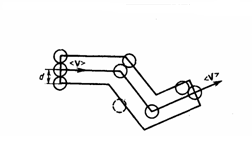
Рис.2

вакум

Газ называется разреженным, если его плотность столь мала, что средняя длина свободного пробега молекул < λ > может быть сравнима с линейными размерами l сосуда, в котором находится газ. Такое состояние газа называется вакуумом.

       Различают следующие степени вакуума: сверхвысокий ( ), высокий ( ), средний ( ) и низкий вакуум.

       Свойства разреженных газов отличаются от свойств неразреженных газов. 

Если из сосуда откачивать газ, то по мере понижения давления число столкновений молекул друг с другом уменьшается, что приводит к увеличению их длины свободного пробега. При достаточно большом разрежении столкновения между молекулами относительно редки, поэтому основную роль играют столкновения молекул со стенками сосуда.

       В состоянии высокого вакуума уменьшение плотности разреженного газа приводит к соответствующей убыли частиц без изменения < λ > . Следовательно, уменьшается число носителей импульса или внутренней энергии в явлениях вязкости и теплопроводности. Коэффициенты переноса в этих явлениях прямо пропорциональны плотности газа. В сильно разреженных газах внутреннее трение, по существу, отсутствует.

       Удельный тепловой поток в сильно разреженных газах пропорционален разности температур и плотности газа.

       Стационарное состояние разреженного газа, находящегося в двух сосудах, соединенных узкой трубкой, возможно при условии равенства встречных потоков частиц, перемещающихся из одного сосуда в другой: , где n₁ и n₂ – число молекул в 1 см³ в обоих сосудах;  и  – их средние арифметические скорости.

       Если Т₁ и Т₂ – температуры газа в сосудах, то предыдущее условие стационарности можно переписать в виде уравнения, выражающего эффект Кнудсена:

где P₁ и P₂ – давления разреженного газа в обоих сосудах.