5. Законы сохранения импульса и и момента импульса

Импульс силы    Векторная физическая величина, являющаяся мерой действия силы за некоторый промежуток времени.  - импульс силы  за малый промежуток времени t. Вектор импульса силы сонаправлен с вектором силы.

[ I ]= Н.с

Закон Сохранения Импульса

Импульсом называют векторную величину, равную произведению массы тела на ее скорость:

При взаимодействии тел замкнутой системы полный импульс системы остается неизменным:

Закон сохранения импульса есть следствие второго и третьего законов Ньютона. Пример использования закона сохранения импульса.

Рассмотрим неупругое столкновение, при котором выполняется закон сохранения импульса. Пусть при абсолютно неупругом столкновении двух тел их скорость будет общей после удара. Ее нужно определить. Напишем векторное уравнение, соответствующее закону сохранения импульса системы:

После проецирования векторов на выбранную ось получим скалярное уравнение, которое позволит определить искомую величину v_общ. Еще один пример - реактивное движение. Рассмотрим простейший случай этого движения, при котором происходит одномоментное взаимодействие - выстрел из винтовки.

До выстрела скорости винтовки и пули были равны нулю. После выстрела они имели различные скорости. Если известна скорость пули, ее масса и масса ружья, можно определить скорость, которую приобрело ружье после выстрела:

Отсюда после проецирования векторов на выбранную ось получим:

Для замкнутой системы тел момент внешних сил всегда равен нулю, так как внешние силы вообще не действуют на замкнутую систему.         Поэтому  , то есть

         или         

       Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени.         Это один из фундаментальных законов природы.         Аналогично для замкнутой системы тел, вращающихся вокруг оси z:

         отсюда                   или          .

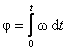6. Гармонические колебания и их характеристики. Квазиупругая сила

Гармонические колебания — колебания, происходящие под действием силы, пропорциональной смещению. Происходят по закону синуса и косинуса. x = x_maxcos(ωt+φ_o), φ = ωt+φ_o, где x — смещение тела от положения равновесия, x — амплитуда колебаний, ω — циклическая частота колебаний, φ_o — начальная фаза, t — время, φ — фаза гармонического колебания.

Скорость и ускорение при гармонических колебаниях.

V(t) = Δx/Δt = x^,(t) (если φ_o=0) V = x^,(t) = x_maxωcos (ωt+π/2) V_max = x_maxω a = V^,(t) = x^,,(t) a = x_maxω²sin (ωt) a_max = x_maxω²

Квазиупругая сила

Квазиупругая сила, направленная к центру О сила F, величина которой пропорциональна расстоянию r от центра О до точки приложения силы; численно F = cr, где с — постоянный коэффициент. Тело, находящееся под действием К. с., обладает потенциальной энергией П = ¹/₂cr². Название "К. с." связано с тем, что аналогичным свойством обладают силы, возникающие при малых деформациях упругих тел (так называемые силы упругости). Для материальной точки, находящейся под действием К. с., центр О является положением устойчивого равновесия. Выведенная из этого положения точка будет совершать около О линейные гармонические колебания или описывать эллипс (в частности, окружность).