Атом во внешнем поле. Диа- и парамагнетизм.
Диа- и парамагнетики
Диамагнетиками называются такие вещества, у которых магнитный момент атома в отсутствии внешнего магнитного поля равен нулю.
при 
Когда
во внешнее магнитное поле помещают
какое-либо вещество, то все атомы этого
вещества оказываются в магнитном поле,
которое изменяет движение электронов
в атоме так, что появляется дополнительный
ток, подобный индукционному току. Если
вектора 
и 
образуют
некоторый угол α, то в магнитном
поле
орбита
электрона начнёт вращаться вокруг
направления
с
некоторой угловой скоростью (
-
ларморова частота прецессии). Такое
движение в механике называют прецессией.
П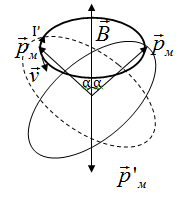
рецессия
электронной орбиты эквивалентна
дополнительному движению электрона
вокруг магнитного поля помимо вращения
вокруг собственной оси и вращения по
орбите. Это дополнительное движение
электрона в магнитном поле и приводит
к возникновению замкнутого индукционного
тока, обладающего магнитным моментом,
который ориентирован всегда против
поля. Таким образом, причина появления
дополнительных магнитных моментов –
прецессия орбиты электрона.
Поскольку диамагнетики намагничиваются против магнитного поля, их намагниченность отрицательна.
К диамагнетикам относятся металлы Bi, Ag, Au, Cu; вода; стекло; инертные газы и др.
Диамагнетизм присущ всем веществам, но у ряда веществ диамагнитный эффект перекрывается более сильными эффектами.
Парамагнетиками называются вещества, у которых атомы в отсутствии внешнего магнитного поля обладают некоторым постоянным магнитным моментом
при
.
Однако,
вследствие теплового движения молекул
их магнитные моменты ориентированы
беспорядочно, поэтому 
.
При наложении магнитного поля возникают
силы, ориентирующие магнитные моменты
каждого атома. Магнитные моменты
стараются выстроиться по полю. Таким
образом, парамагнетик намагничивается,
создавая собственное магнитное поле,
сонаправленное с внешним полем и
усиливающего его.
Процесс ориентации магнитных моментов атомов во внешнем магнитном поле называется парамагнитным эффектом.
В парамагнетике выстраивающие силы относительно малы по сравнению с силами теплового движения, которые стремятся разрушить упорядочение. Поэтому с понижением температуры магнитная восприимчивость парамагнетиков обычно возрастает.
К парамагнетикам относятся: редкоземельные металлы, Pt, Al, Mg, Cr, O2 и др.
Вектор намагничивания. Магнитное поле в веществе.
Намагни́ченность — векторная физическая величина, характеризующая магнитное состояние макроскопического физического тела. Обозначается обычно М или J. Определяется как магнитный момент единицы объёма вещества:
Здесь, M — вектор намагниченности; m - вектор магнитного момента; V — объём.
В общем случае (случае неоднородной, по тем или иным причинам, среды) намагниченность выражается как
и является функцией координат.
Связь между M и напряженностью магнитного поля H в диамагнитных и парамагнитных материалах, обычно линейна (по крайней мере, при не слишком больших величинах намагничивающего поля):
где χm называют магнитной восприимчивостью. В ферромагнитных материалах нет однозначной связи между M и H из-за магнитного гистерезиса.
Магнитная индукция определяется через намагниченность как:
(в
системе СИ)
(в
системе СГС)
Магнитное поле в веществе |
|
|
|
При изучении магнитного поля в веществе различают два типа токов – макротоки и микротоки. Макротоками называются токи проводимости и конвекционные токи, связанные с движением заряженных макроскопических тел. Микротоками (молекулярными токами) называют токи, обусловленные движением электронов в атомах, молекулах и ионах. Магнитное поле в веществе является суперпозицией двух полей: внешнего магнитного поля, создаваемого макротоками и внутреннего, или собственного, магнитного поля, создаваемого микротоками. Характеризует
магнитное поле в веществе вектор
Количественной
характеристикой намагниченного
состояния вещества служит векторная
величина – намагниченность
где Для
того чтобы связать вектор намагниченности
среды
с
током
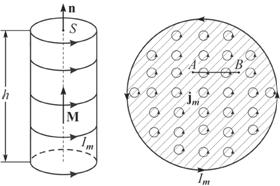
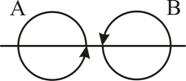
а б в Рис. 6.3 Каждый атомный ток в плоскости сечения стержня, перпендикулярной его оси, представляет микроскопический кружок, причем все микротоки текут в одном направлении – против часовой стрелки (рис. 6.3, б). В местах соприкосновения отдельных атомов и молекул (А, В) молекулярные токи противоположно направлены и компенсируют друг друга (рис.6.3, в). Нескомпенсированными остаются лишь токи, текущие вблизи поверхности материала, создавая на поверхности материала некоторый микроток , возбуждающий во внешнем пространстве магнитное поле, равное полю, созданному всеми молекулярными токами. Закон полного тока для магнитного поля в вакууме можно обобщить на случай магнитного поля в веществе:
где
и Как видно из рисунка 6.4, вклад в дают только те молекулярные токи, которые нанизаны на замкнутый контур L.
Рис. 6.4 Алгебраическая сумма сил микротоков связана с циркуляцией вектора намагниченности соотношением
тогда закон полного тока можно записать в виде
Вектор
называется напряженностью магнитного поля. Таким
образом, закон
полного тока для
магнитного поля в веществе утверждает,
что циркуляция
вектора напряженности магнитного
поля
Выражение (6.3.6) – это закон полного тока в интегральной форме. В дифференциальной форме его можно записать:
Намагниченность изотропной среды с напряженностью связаны соотношением:
где |
,
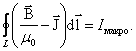равный геометрической сумме 
и 
магнитных
полей:
,
,
равная отношению магнитного момента
малого объема вещества к величине
этого объема:
,
–
магнитный момент i-го
атома из числа n атомов,
в объеме ΔV.
,
рассмотрим равномерно намагниченный
параллельно оси цилиндрический
стержень длиной h и
поперечным сечением S (рис.
6.3, а). Равномерная намагниченность
означает, что плотность атомных
циркулирующих токов внутри
материала
повсюду
постоянна.
,
–
алгебраическая сумма макро- и микротоков
сквозь поверхность, натянутую на
замкнутый контур L.
,
,
вдоль
произвольного замкнутого контура L
равна алгебраической сумме макротоков
сквозь поверхность, натянутую на этот
контур:
,
,
,
–
коэффициент пропорциональности,
характеризующий магнитные свойства
вещества и называемый магнитной
восприимчивостью среды.
Он связан с магнитной проницаемостью
соотношением 