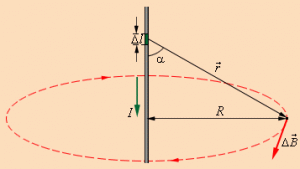
36. Закон Био-Савара-Лапласа и его применение. Закон Био Савара Лапласа — Магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемая отдельными участками токов.

  

Яндекс.ДиректВсе объявления

Законы РФ-Советы юриста онлайнЗаконы РФ – Бесплатные консультации юриста онлайн. Спрашивайте!juristplus.ru Санкт-Петербург

Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:

  

Закон Био-Савара-Лапласа для некоторых токов:

Магнитное поле прямого тока :    

Магнитное поле кругового тока :    

В формуле мы использовали :

 — Магнитная индукция

 — Вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током

 — Магнитная постоянная

 — Относительная магнитная проницаемость (среды)

 — Сила тока

 — Расстояние от провода до точки, где мы вычисляем магнитную индукцию

 — Угол между вектором dl и r

37. Циркуляция вектора индукции магнитного поля.

По определению циркуляцией вектора   по замкнутому контуру   называется интеграл  , знак которого зависит от направления обхода контура. Циркуляция вектора   по любому замкнутому контуру равна алгебраической сумме токов, охватываемых этим контуром, умноженной на магнитную постоянную: .

Это - теорема о циркуляции для вектора индукции магнитного поля.

Или  . Это – теорема о циркуляции в дифференциальной форме, где 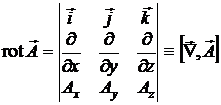 , то есть   - это векторное произведение оператора 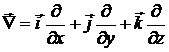 и вектора  .

Зная индукцию   как функцию координат, можно простым дифференцированием определить плотность тока   в каждой точке пространства, то есть определить распределение токов, создающих данное магнитное поле.

38. Закон Ампера. Закон Ампера — Если провод, по которому течет ток, находится в магнитном поле, то на каждый из носителей тока действует сила Ампера

  

Закон Ампера в векторной форме

  

Закон Ампера устанавливает, что на проводник с током, помещенный в однородное магнитное поле, индукция которого В, действует сила, пропорциональная силе тока и индукции магнитного поля

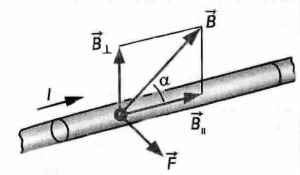
Сила Ампера направлена перпендикулярно плоскости, в которой лежат векторы dl и B. Для определения направления силы, действующей на проводник с током, помещенный в магнитное поле, применяется правило левой руки.

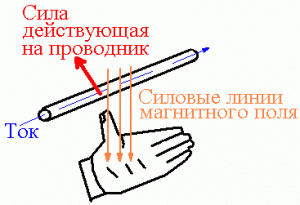
Чтоб найти силу Ампера для двух бесконечных параллельных проводников, токи которых текут в одном направлении и эти проводники находятся на расстоянии r, необходимо :

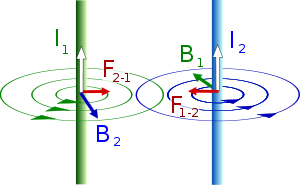
Бесконечный проводник с током I1 в точке на расстоянии r создаёт магнитное поле с индукцией:

По закону Био-Савара-Лапласа для прямого тока :    

Теперь по закону Ампера найдём силу, с которой первый проводник действует на второй:

  

По правилу буравчика,  направлена в сторону первого проводника (аналогично и для  , а значит, проводники притягиваются).

  

Интегрируем, учитывая только проводник единичной длины (пределы l от 0 до 1) и сила Ампера получается:

  

В формуле мы использовали :

 — Сила Ампера

 — Скорость хаотического движения носителя

 — Скорость упорядоченного движения

 — Магнитная постоянная

 — Относительная магнитная проницаемость (среды)

 — Магнитная индукция

 — Элементарная длина провода

 — Угол между векторами dl и B