6. Ограниченность функции

Функция , называется ограниченной на множестве X, если существуют числа m и M такие, что .

Число называется точной нижней гранью функции f, а число - точной верхней гранью функции f на множестве M. Разность M0 - m0 называется колебанием функции f на множестве X.

Если функция f: X → R имеет конечный предел в точке , то она ограничена в некоторой окрестности этой точки.

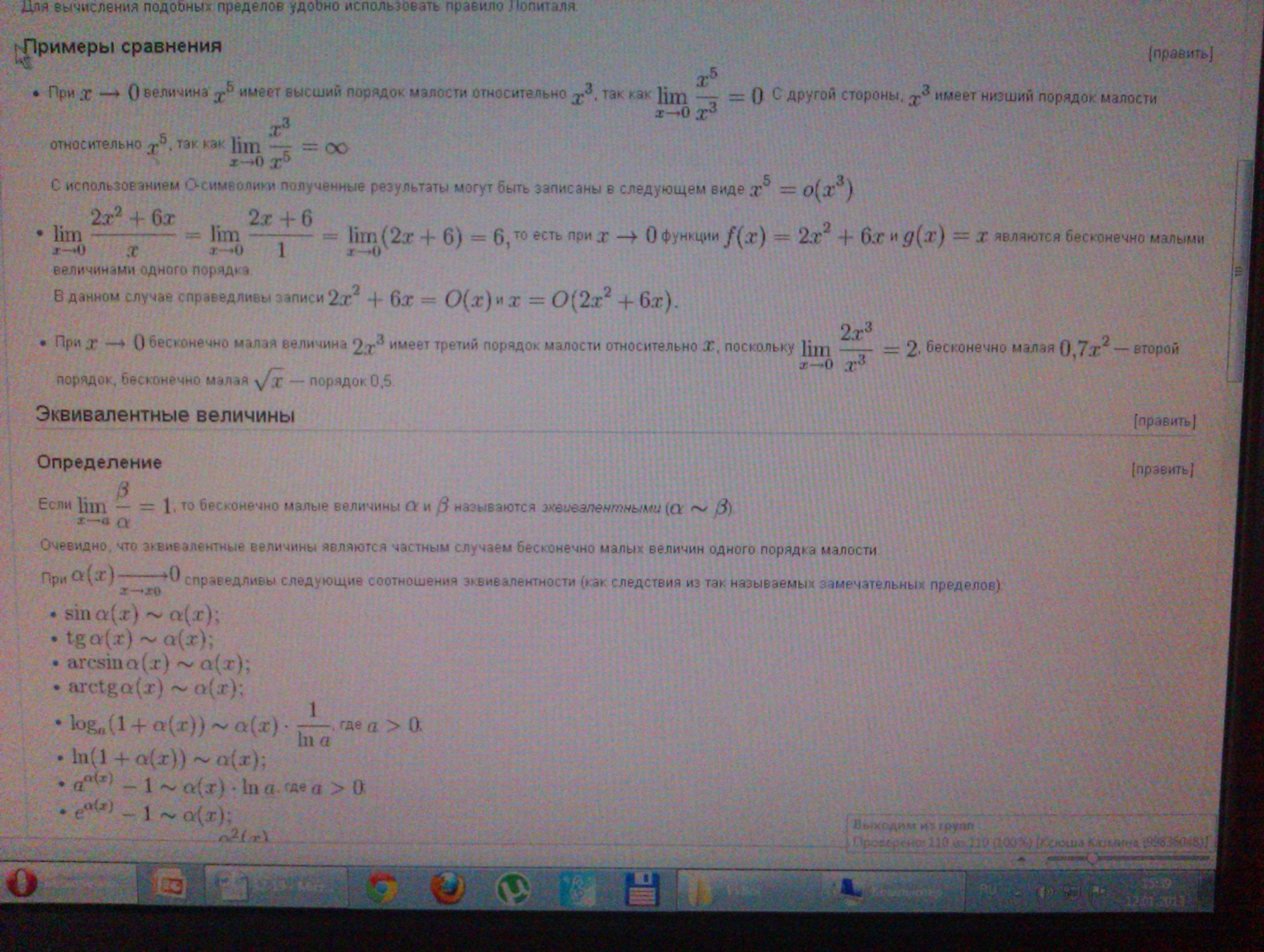
Теорема (следствие теоремы о пределе на бесконечности произведения бесконечно малой и ограниченной последовательностей)

Пусть {A(n)} и {B(n)} - бесконечно малые. Тогда {A(n)B(n)} - бесконечно малая.

9Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.

Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.

10.

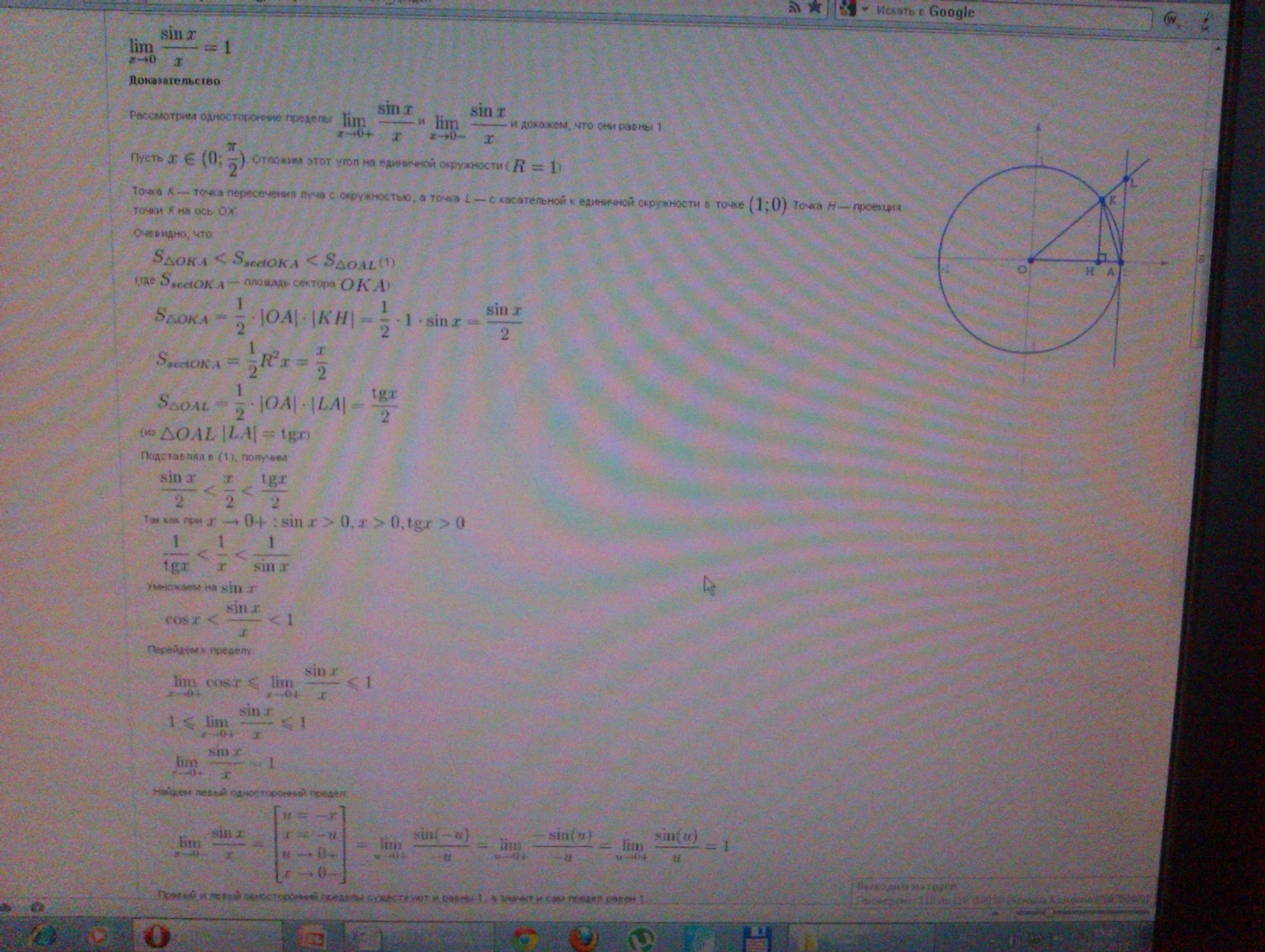
Первый замечательный предел.

12.На оси Х – две точки: x0 и x1 (рис.1). Если от x1 отнимем x0, то узнаем длину шага между ними – а говоря иначе, узнаем, на сколько приросла точка x0 в точке x1. Эта разность между двумя заданными точками оси X и называется приращением аргумента.

Точки x0 и x1 образуют на оси Y соответственно точки у0 и у1. Если от у1 отнять у0, то мы получим приращение функции.

Итак, в функции y = f(x) относительно определенных точек x0 и x1:

разность x1 – x0 называется приращением аргумента, а разность у1 – у0 называется приращением функции.

Но у0 и у1 – зависимые переменные (зависимые от значений х). То есть их правильно записывать так: f(x0) и f(x1). Следовательно, приращение функции – это разность f(x1) – f(x0).

Приращение обозначается греческой буквой Δ (дельта):

Δx = x1 – x0;

Δy (или Δ f) = f(x1) – f(x0).

Можно сказать и иначе: если к x0 прибавить величину приращения Δx, то мы получим точку x1.

То есть x1 = x0 + Δx (рис.2).

Тогда точку f(x1), отмеченную на первом рисунке как у1, тоже можно обозначить иначе:

f(x0 + Δx).

Осталось вывести формулу приращения функции.

Формула приращения функции:

Δy = f(x0 + Δx) – f(x0)

или

Δf = f(x0 + Δx) – f(x0)

Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.

13.Свойство. Сумма конечного числа непрерывных функций есть функция непрерывная.

Непрерывность функции в точке равносильна её непрерывно-

сти в этой точке и справа и слева.

Отметим, что приведенные выше свойства функций, непре-

рывных в точке, распространяются на функции, непрерывные

справа или слева.

14.

Непрерывность функции в точке и на множестве

Определение 1 Функция yfx=() называется непрерывной в точке x0, если выполняются следующие три условия :

1) функция определена в точке , т.е. yfx=()x0x0∈Df().

2) существует lim()xxfx→0

3) lim()()xxfxfx→=00

Если в точке нарушено хотя бы одно из условий то функция называется разрывной в точке , а точка называется x0x0x0 точкой разрыва

Определение 2 Функция называется yfx=()непрерывной в точке x0, если

∀>∃>∀−<⇒−<εδδ0000 :()xxxfxfx

Так как xxx−=0Δ-приращение аргумента, а fxfxy()()−=0Δ-приращение функции в точке то x0

функция непрерывна в точке , если для yfx=()x0∀>∃>εδ00 ΔΔxy<⇒<δε т.е. Δпри . y→0Δx→0 x000xy0)(lim0xfxfxx=→f(x)

Определение 3 Функция yfx=() называется непрерывной в точке x0, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е.

limΔΔxy→=00

Определение 4 Функцияyfx=(), непрерывная во всех точках множества Х, называется непрерывной на этом множестве

17.

17.

10.

23. Асимптота кривой – это прямая, к которой кривая приближается сколь угодно близко при удалении в бесконечность. Представьте себе мчащийся по прямолинейному шоссе автомобиль и всадника, скачущею по полю с той же скоростью, но направленной в каждый момент на автомобиль. Маршрут всадника в этом случае будет кривой линией, называемой трактрисой, для которой линия шоссе является асимптотой.

Виды

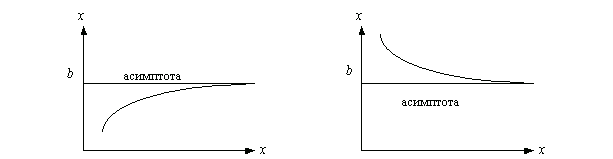
3.1 Горизонтальная асимптота

Пусть $ lim f (x) = b. Тогда говорят, что у функции f (x) имеется горизонтальная асимптота y = b. График функции чаще всего имеет такой вид (при x ® +¥) (рис.2)

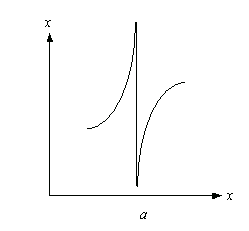
Вертикальная асимптота

Пусть при x ® a ± 0 lim f (x) = ± ¥. Тогда говорят, что прямая x = a является

х ® ¥

вертикальной асимптотой f (x). График функции f (x) при приближении x к а ведёт примерно так (рис.4), хотя, конечно, могут быть разные варианты, связанные с тем, куда уходит f (x) в + ¥ или - ¥.

Чаще всего вертикальная асимптота появляется тогда, когда f (x) имеет вид

.

Тогда вертикальные асимптоты находятся как корни уравнения

Наклонная асимптота

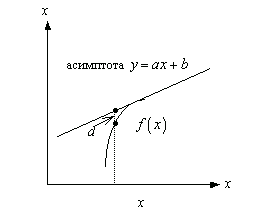усть уравнение асимптот есть y = ax + b. Значение функции при аргументе х есть d = ax + b – f (x). Неограниченное приближение к асимптоте означает, что величина d = ax + b – f (x) стремится к 0 при х ® ± ¥

lim [f (x) – (ax + b)] = 0.

x ® ¥

Если эта величина стремится к нулю, то тем более стремится к нулю величина

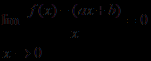
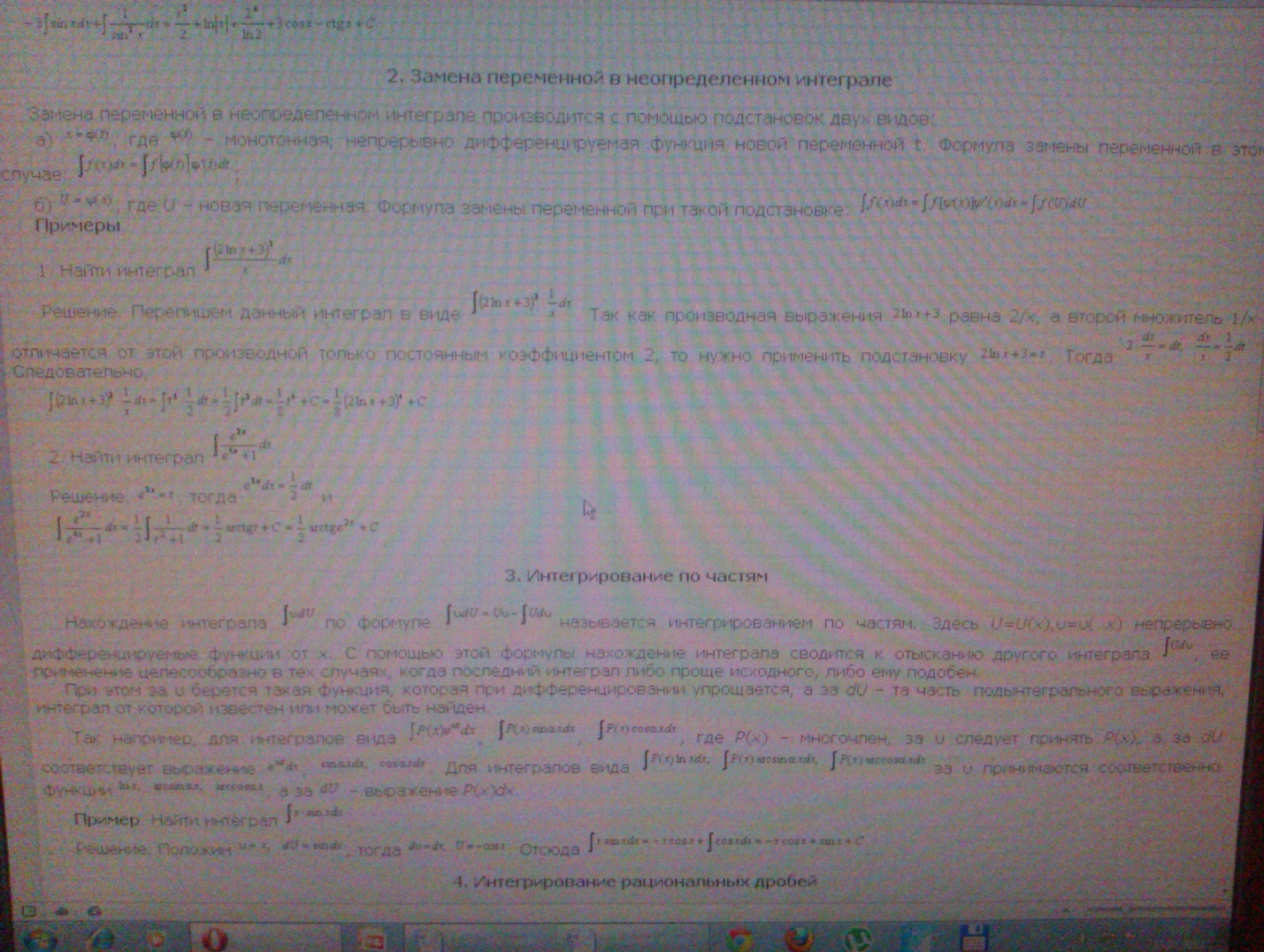
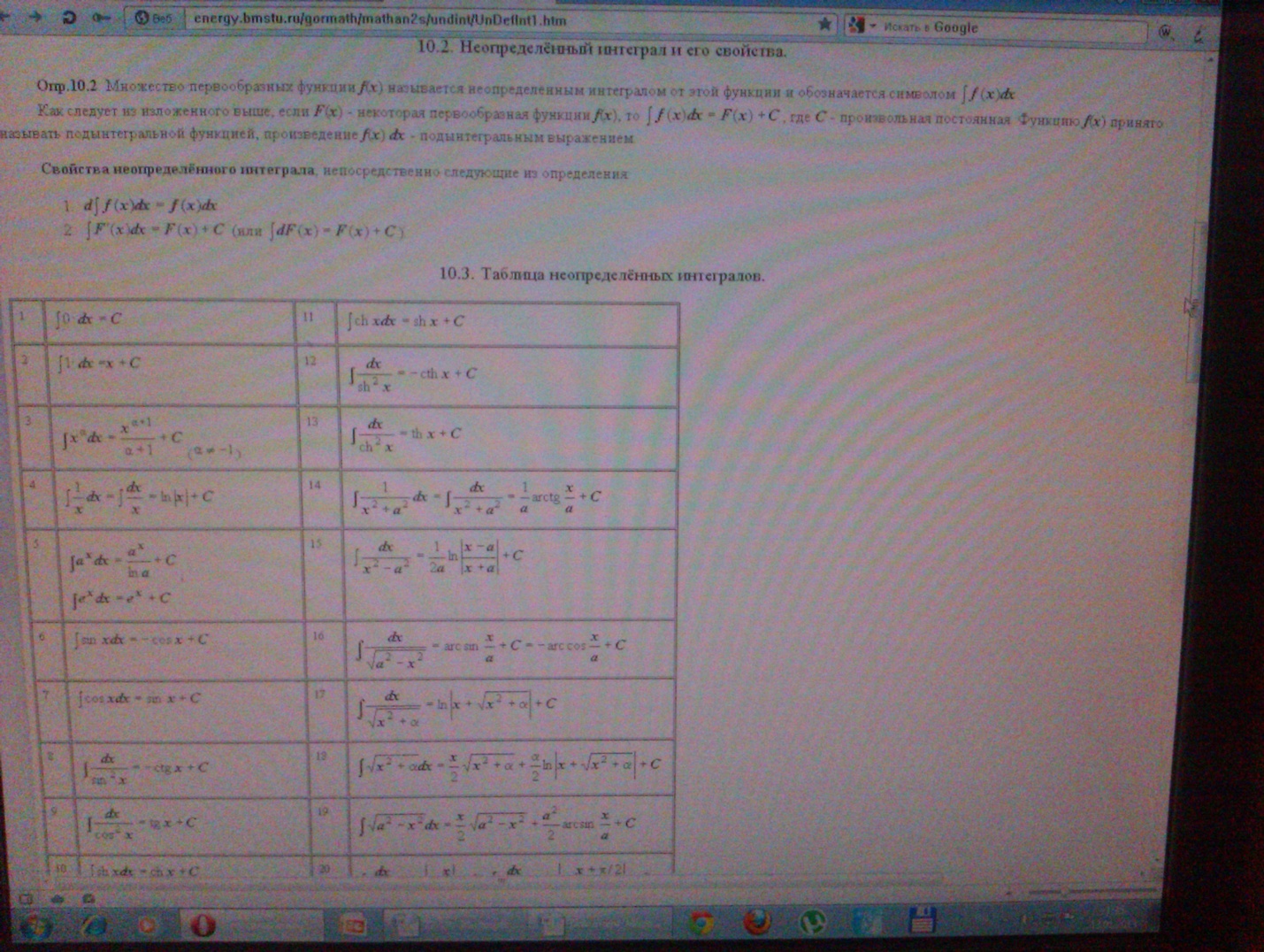
№1. Первообра́зной[1] или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Свойства первообразной

Первообразная суммы равна сумме первообразных

Первообразная произведения константы и функции равна произведению константы и первообразной функции

Достаточным условием существования первообразной у заданной на отрезке функции является непрерывность на этом отрезке

Необходимыми условиями существования являются принадлежность функции первому классу Бэра и выполнение для неё свойства Дарбу

У заданной на отрезке функции любые две первообразные отличаются на постоянную.

2.