12.Уравнение линии на плоскости R2

Уравнением линии на плоскости Оху называется равенство, со-

держащее переменные х и у, вида F(х, у) = 0, которому удовлетворя-

ют все точки данной линии и только они. Для вывода уравнения ли-

нии часто используются формулы:

а) расстояние между двумя точками ( ) 1 1 1 М х , у и ( , ). 2 2 2 М х у

2

2 1

2

2 1 d = (х − х ) + ( у − у ) (5.1)

б) деление отрезка в данном отношении: если точка М(х, у) делит

отрезок, определяемый точками ( ) 1 1 1 М х , у и ( , ). 2 2 2 М х у в отношении

= λ

2

1

ММ

М М , то координаты точки М определяются по формулам:

λ

λ

+

+

=

1

1 2 х х х ,

λ

λ

+

+

=

1

1 2 у у у . (5.2)

В частности, если точки М – середина отрезка , 1 2 М М то λ = 1 и

формулы (5.2) принимают вид:

2

1 2 х х х +

= ,

2

1 2 у у у +

= . (5.3)

Пример 5.1. Найти уравнение множества точек, равноудаленных

от точек А(1; 3) и B (3; 1).

Решение. Пусть М(х, у) – произвольная точка искомой линии,

тогда, согласно условию, имеем АМ = ВМ или по (5.1)

(х −1)2 + ( у − 3)2 = (х − 3)2 + ( у −1)2 .

Возведя обе части равенства в квадрат и упрощая, получим

х2 – 2х + 1 + у2 – 6у + 9 = х2 – 6х + 9 + у2 – 2у + 1,

откуда получаем у = х . Это серединный перпендикуляр, восставлен-

ный из середины отрезка АВ.

В пространстве задана декартова прямоугольная система координат. Рассмотрим сферу радиуса R, с центром в точке А(а,в,с). Сфера- множество точек, отстоящих от центра на одном и том же расстоянии R. Обозначим через M(x,y,z) произвольную точку на сфере, радиуса R, тогда . Мы получим две точки:

(1).

Возведя в квадрат обе части равенства (1), мы получим более удобную формулу:

(2).

Равенство (2) называется уравнением сферы с центром в точке А(а,в,с) и радиуса R.

Определим теперь, что следует вообще понимать под уравнением некоторого множества. Пусть выбрана система координат. Под уравнением множества S в этой системе координат мы будем понимать выражение определения S через координаты его точек, т.е. высказывание, верное для координат точек, принадлежащих S, и неверное для координат точек, ему не принадлежащих.

Вывод уравнения окружности

Окружностью называется геометрическая фигура, состоящая из всех то-

чек плоскости, расположенных на заданном (одинаковом) расстоянии от дан-

ной точки.

Данная точка называется центром окружности, а отрезок, соединяющий

центром с какой-либо точкой окружности, – радиусом окружности.

Уравнением фигуры в прямоугольной системе координат на плоскости

называется уравнение с двумя переменными х и у, которому удовлетворяют ко-

ординаты любой точки фигуры и не удовлетворяют координаты точек, не при-

надлежащих этой фигуре.

Выведем уравнение окружности радиуса r с центром С в заданной прямо-

угольной системе координат. Пусть точка С имеет координаты (хо; уо) (рис. 1).

Рис. 1

Расстояние от произвольной точки М (х; у) до точки С (хо; уо) вычисляет-

ся по формуле МС х хо у уо .

2 2

Если точка М лежит на окружности, то МС = r, или МС2 = r2, то есть ко-

ординаты точки М удовлетворяют уравнению

(х – хо)2 + (у – уо)2 = r2. (1)

Если точка М (х; у) не лежит на данной окружности, то МС2 r2, и коор-

динаты точки М не удовлетворяют уравнению (1).

Следовательно, прямоугольной системе координат уравнение окружности

радиуса r с центром в точке С (хо; уо) имеет вид

(х – хо)2 + (у – уо)2 = r2.

Если центром окружности радиуса r является начало координат, то урав-

нение примет вид

х2 + у2 = r2.





х

у

r

С хо ; уо

Мх ; у

О

Если центр окружности радиуса r лежит на оси абсцисс, то уравнение

примет вид

(х – хо)2 + у2 = r2.

Если центр окружности радиуса r лежит на оси ординат, то уравнение

примет вид

х2 + (у – уо)2 = r2.__

Пусть центр сферы находится в точке A (a; b; c), а радиус сферы равен R. Точками сферы являются те и только те точки пространства, расстояние от которых до точки A равно R. Квадрат расстояния от любой точки B (x; y; z) сферы до точки A равен

(x – a)2 + (y – b)2 + (z – c)2.

Поэтому уравнение сферы с центром A (a; b; c) и радиусом R имеет вид:

(x – a)2 + (y – b)2 + (z – c)2 = R2.

13. Векторно-параметрическое уравнение прямой

где - фиксированная точка, лежащая на прямой; - направляющий вектор (см. рис. 4.11).

В координатах (параметрические уравнения):

16 Взаимное расположение прямой и плоскости

Пусть прямая L задана уравнениями (5.17), а плоскость Р – урав-

нением (5.25). Углом между прямой L и плоскостью Р называется

угол φ, образованный прямой L и ее проекцией на плоскость Р. Для

вычисления угла φ используется формула

2 2 2 2 2 2

( , )

sin

A B C m n p

Am Bn Cp

n S

n S

+ + + +

+ +

φ = = . (5.33)

Если выполняется равенство

Аm + Bn + Ср = 0, (5.34)

то прямая L и плоскость Р параллельны. Если же справедливы соот-

ношения

p

C

n

B

m

A = = , (5.35)

то прямая L и плоскость Р перпендикулярны.

Если условие (5.34) не выполняется, то прямая и плоскость пере-

секаются в единственной точке М1 = (х1, у1, z1). Координаты этой точ-

ки найдутся из равенств:







= +

= +

= +

,

1 1

1 1

1 1

z z рt

у у nt

х х mt

о

о

о

(5.36)

где t1 есть то единственное значение параметра t, при котором прямая

L и плоскость Р пересекаются:

Am Bn Cp

t Axo Byo Czo D

+ +

+ + +

= 1 .

Если Аm + Вn + Ср = 0 и Ахо + Вуо + Сzо + D ≠ 0, то прямая L и плос-

кость Р параллельны (они не пересекаются ни при одном значении t).

Если Аm + Вn + Ср = 0 , Ахо + Вуо + Сzо + D = 0, то прямая L лежит на

плоскости Р (они имеютбесчисленноемножествоточек пересечения).

14.

http://courses.edu.nstu.ru/getfile.php?curs=1735&file_id=16818

лекция №8

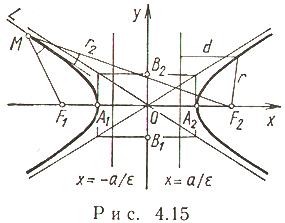
18. Пусть на плоскости заданы две точки ф1и ф2 и дано число a (0 < a < c). Гипербола - множество точек M плоскости, для каждой из которых модуль разности расстояний от точек и равен 2a. Точки и называются фокусами гиперболы; - действительная ось; - мнимая ось; O - центр; - левый и правый фокусы; - вершины; - фокальные радиусы:

Каноническое уравнение:

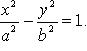
http://www.pm298.ru/2step5.php

19. Поверхности второго порядка

Поверхности второго порядка – это поверхности, которые в прямоугольной

системе координат определяются алгебраическими уравнениями второй степени.

1. Эллипсоид.

Эллипсоидом называется поверхность, которая в некоторой прямоугольной

системе координат определяется уравнением: [pic]

(1)

Уравнение (1) называется каноническим уравнением эллипсоида.

Установим геометрический вид эллипсоида. Для этого рассмотрим сечения

данного эллипсоида плоскостями, параллельными плоскости Oxy. Каждая из

таких плоскостей определяется уравнением вида z=h, где h – любое число, а

линия, которая получается в сечении, определяется двумя уравнениями

[pic] (2)

Исследуем уравнения (2) при различных значениях h.

1) Если [pic]> c (c>0), то [pic] и уравнения (2) определяют мнимый эллипс,

т. е. точек пересечения плоскости z=h с данным эллипсоидом не существует.

2) Если [pic], то [pic] и линия (2) вырождается в точки (0; 0; + c) и (0;

0; - c) (плоскости [pic] касаются эллипсоида).

3) Если [pic], то уравнения (2) можно представить в виде

[pic]

откуда следует, что плоскость z=h пересекает эллипсоид по эллипсу с

полуосями [pic] и [pic]. При уменьшении [pic] значения [pic]и

[pic]увеличиваются и достигают своих наибольших значений при [pic], т. е. в

сечении эллипсоида координатной плоскостью Oxy получается самый большой

эллипс с полуосями [pic] и [pic].

Аналогичная картина получается и при пересечении данной поверхности

плоскостями, параллельными координатным плоскостям Oxz и Oyz.

Таким образом, рассмотренные сечения позволяют изобразить эллипсоид как

замкнутую овальную поверхность (рис. 156). Величины a, b, c называются

полуосями эллипсоида. В случае a=b=c эллипсоид является сферой.