3. Искусственные нейронные сети

1. Основные проблемы, решаемые искусственными нейронными сетями

Искусственные нейронные сети (ИНС) строятся по принципам организа­ции и функционирования их биологических аналогов. Они способны решать широкий круг задач распознавания образов, идентификации, прогнозирова­ния, оптимизации, управление сложными объектами. Дальнейшее повыше­ние производительности компьютеров все в большей мере связывают с ИНС, в частности, с нейрокомпьютерами (НК), основу которых составляет искус­ственная нейронная сеть.

Глубокое изучение ИНС требует знания нейрофизиологии, науки о по­знании, психологии, физики (статистической механики), теории управления, теории вычислений, проблем искусственного интеллекта, статистики, мате­матики, распознавания образов, компьютерного знания, параллельных вы­числений и аппаратных средств (цифровых и аналоговых). С другой сто­роны, ИНС также стимулируют эти дисциплины, обеспечивая их новыми

инструментами и представлениями. Этот симбиоз жизненно необходим для исследования нейронных сетей.

Представим некоторые проблемы, решаемые искусственными нейронны­ми сетями.

1. Классификация образов. Задача классификации состоит в указании при­надлежности некоторого входного образа, представленного вектором признаков, одному или нескольким предварительно определенным клас­сам. К известным приложениям относятся распознавание букв, распо­знавание речи, классификация сигнала электрокардиограммы, класси­фикация клеток крови.

2. Кластеризация/категоризация. При решении задачи кластеризации, ко­торая известна также как классификация образов без учителя, отсут­ствует обучающая выборка с метками классов. Алгоритм кластеризации основан на подобии образов и размещает близкие образы в один кла­стер. Известны случаи применения кластеризации для извлечения зна­ний, сжатия данных и исследования свойств данных.

3. Аппроксимация функции. Предположим, что имеется обучающая выбор­ка, которая генерируется неизвестной функцией, искаженной шумом. За­дача аппроксимации состоит в нахождении оценки этой функции.

4. Прогнозирование. Пусть в последовательные моменты времени t]_,t₂,..., tN заданы N дискретных отсчетов {y(t₁),... ,y(tN)}. Задача состоит в предсказании значения y(tN +i) в момент tN +₁. Прогноз имеет значитель­ное влияние на принятие решений в бизнесе, науке и технике.

5. Оптимизация. Многочисленные проблемы в математике, статистике, технике, науке, медицине и экономике могут рассматриваться как про­блемы оптимизации. Задачей оптимизации является нахождение реше­ния, которое удовлетворяет системе ограничений и максимизирует или минимизирует целевую функцию.

6. Память, адресуемая по содержанию. В модели вычислений фон Нейма­на обращение к памяти доступно только посредством адреса, который не зависит от содержания памяти. Более того, если допущена ошибка в вы­числении адреса, то может быть найдена совершенно иная информация. Память, адресуемая по содержанию, или ассоциативная память, доступ­на по указанию заданного содержания. Содержимое памяти может быть вызвано даже по частичному или искаженному содержанию. Ассоциа­тивная память чрезвычайно желательна при создании перспективных информационно-вычислительных систем.

7. Управление. Рассмотрим динамическую систему, заданную {u(t),y(t)}, где u(t) является входным управляющим воздействием, a y(t) — выходом системы в момент времени t. В системах управления с эталонной мо­делью целью управления является расчет такого входного воздействия u(t), при котором система следует по желаемой траектории, диктуемой эталонной моделью.

2. Классификация ИНС

Нейронная сеть представляет собой совокупность нейроподобных элементов, определенным образом соединенных друг с другом и с внешней средой с помощью связей, определяемых весовыми коэффициентами.

С точки зрения топологии можно выделить три основных типа нейрон­ных сетей.

1. Полносвязные сети, в которых каждый нейрон передает свой выходной сигнал остальным нейронам, в том числе и самому себе.

2. Слабосвязные (с локальными связями) сети, где нейроны располагают­ся в узлах прямоугольной и гексагональной решетки.

3. Многослойные нейронные сети — в данных сетях нейроны объединяют в слои.

В свою очередь, среди многослойных нейронных сетей выделяют следу­ющие типы:

• сети без обратных связей (прямого распространения) — в таких сетях, называемых многослойным персептроном, нейроны входного слоя полу­чают входные сигналы, преобразуют их и передают нейронам первого скрытого слоя, и так далее вплоть до выходного, который выдает сигна­лы для интерпретатора и пользователя;

• сети с обратными связями (рекуррентные), в которых информация с последующих слоев передается на предыдущие.

Мы будем рассматривать и изучать далее многослойные сети прямого распространения.

3. Нейрон как составная часть ИНС

Нейрон является составной частью нейронной сети. Он состоит из элементов трех типов: умножителей (синапсов), сумматора и нелинейного преобразо­вателя. Синапсы осуществляют связь между нейронами, умножают входной сигнал на число, характеризующее силу связи (вес синапса). Сумматор вы­полняет сложение сигналов, поступающих по синаптическим связям от дру­гих нейронов, и внешних входных сигналов. Нелинейный преобразователь реализует нелинейную функцию одного аргумента — выхода сумматора. Эта функция называется функцией активации или передаточной функцией. На рис. 10 приведено строение одного нейрона.

Нейрон в целом реализует скалярную функцию векторного аргумента. Математическая модель нейрона:

n

s = ^ ад + b,

i=i

где Wi — вес синапса; i = 1,..., n; b — значение смещения; s — результат сум­мирования; x_i есть i-й компонент входного вектора (входной сигнал), i = = 1,..., n; y — выходной сигнал нейрона; n — число входов нейрона,; f (s) — нелинейное преобразование (функция активации).

Рис. 10. Нейрон

В общем случае входной сигнал, весовые коэффициенты и смещение мо­гут принимать действительные значения, а во многих практических зада­чах—лишь некоторые фиксированные значения. Выход определяется видом функции активации и может быть как действительным, так и целым.

В качестве функции активации нейронов берут обычно одну из следую­щих:

• пороговая функция активации;

• экспоненциальная сигмоида;

• рациональная сигмоида;

• гиперболический тангенс.

Вид этих функций будет описан в следующем разделе.

Данные функции активации обладают таким важным свойством как нели­нейность. Нелинейность функции активации принципиальна для построения нейронных сетей. Если бы нейроны были линейными элементами, то любая последовательность нейронов также производила бы линейное преобразова­ние и вся нейронная сеть была бы эквивалентна одному нейрону (или одно­му слою нейронов в случае нескольких выходов). Нелинейность разрушает суперпозицию и приводит к тому, что возможности нейросети существенно выше возможностей отдельных нейронов.

4. Архитектура многослойной сети прямого распространения

Опишем самую популярную архитектуру — многослойный персептрон с по­следовательными связями и сигмоидальной функцией активации (Feedforward Artifitial Neural Network, FANN).

В многослойных нейронных сетях с последовательными связями нейро­ны делятся на группы с общим входным сигналом — слои. Стандартная сеть

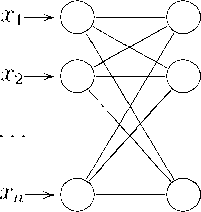
состоит из L слоев, пронумерованных слева направо. Каждый слой содер­жит совокупность нейронов с едиными входными сигналами. Внешние вход­ные сигналы подаются на входы нейронов входного слоя (его часто нумеру­ют как нулевой), а выходами сети являются выходные сигналы последнего слоя. Кроме входного и выходного слоев в многослойной нейронной сети есть один или несколько скрытых слоев, соединенных последовательно в прямом направлении и не содержащих связей между элементами внутри слоя и об­ратных связей между слоями. Число нейронов в слое может быть любым и не зависит от количества нейронов в других слоях. Архитектура нейронной сети прямого распространения сигнала приведена на рис. 11.

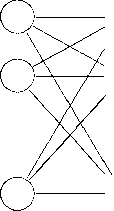
O^V2

О^Уп

Рис. 11. Архитектура многослойной сети

На каждый нейрон первого слоя подаются все элементы внешнего вход­ного сигнала. Все выходы нейронов i-го слоя подаются на каждый нейрон слоя i + 1.

Нейроны выполняют взвешенное суммирование элементов входных сиг­налов. К сумме прибавляется смещение нейрона. Над результатом суммиро­вания выполняется нелинейное преобразование — функция активации (пере­даточная функция). Значение функции активации есть выход нейрона. При­ведем схему многослойного персептрона. Нейроны представлены кружками, связи между нейронами — линиями со стрелками.

Функционирование сети выполняется в соответствии с формулами:

N_k-

L;

_s[k] _ ^sj _

Е wjk^]y'^k—1] + j^], j _1,...,Nk, k _1,..

i = 1

j _ f j, j _1,...,Nk, k _ 1,... ,L — 1,

[L] [L]

где

yj _ ^sj ,

yf ^1] — выходной сигнал i-го нейрона (k — 1)-го слоя;

wj_i —вес связи между j-м нейроном слоя (k — 1) и i-м нейроном k-го слоя;

bj^k] — значение смещения j-го нейрона k-го слоя;

y = f (s) — функция активации;

[k] „ , yj — выходной сигнал j-го нейрона k-го слоя;

Nk — число узлов слоя k;

L — общее число основных слоев;

n = N₀ — размерность входного вектора;

m = Nl — размерность выходного вектора сети.

На рис. 12 представлена сеть прямого распространения сигнала с пятью входами, тремя нейронами в скрытом слое и двумя нейронами в выходном слое.

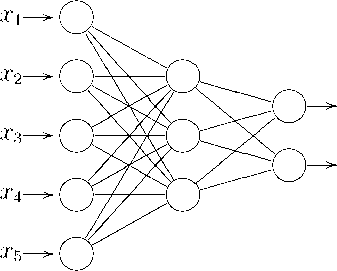
Рис. 12. Пример нейронной сети

5. Функции активации

В качестве функции активации нейронов берут обычно одну из следующих.

1. Пороговая функция активации

f (s) = l^{h s 1 0}

^w [0, s< 0.

Эта функция имеет разрыв первого рода в точке x = 0. График этой функции приведен на рис. 13(a).

2. Экспоненциальная сигмоида f (s) = ₁₊₍1-_as (рис. 13(b)). При уменьшении

параметра а сигмоида становится более пологой, вырождаясь в горизон­тальную линию на уровне 0.5 при а = 0. При увеличении а сигмоида все больше приближается к функции единичного скачка.

3. Рациональная сигмоида f (s) = -щ+а. График этой функции приведен на рис. 13(c).

S _ S

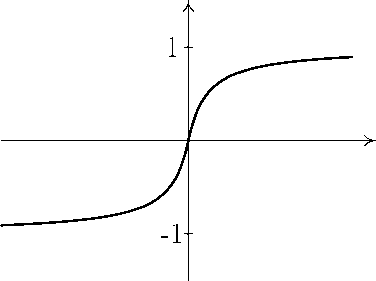
(c) рациональная сигмоида

Рис. 13. Графики различных функций активации

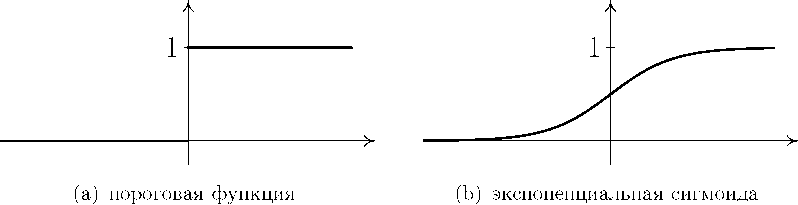
4. Гиперболический тангенс f (s) = th^s = ^e°S ^-e_ 1.

¹ j \ / a e a +e a

Здесь a — некоторый параметр.

В отличие от пороговой функции активации, три последние функции яв­ляются непрерывными, и более того, бесконечно дифференцируемыми. При решении практических задач чаще используют экспоненциальную сигмоиДу, и реже — гиперболический тангенс, так как для его реализации требуется большее число тактов работы ЭВМ. Кроме того, сигмоидальные функции обладают таким важным свойством как нелинейность.

6. Обучение многослойной сети прямого распространения

Если все параметры многослойной сети прямого распространения зафик­сированы, то есть W = {wj}, B = j — заданы, то многослойная сеть

прямого распространения осуществляет отображение пространства Rⁿ в про­странство R^m. Обозначим это отображение:

y = N(x, W, B),

где W, B — параметры отображения; x Е Rⁿ — аргумент отображения; у Е R^m — образ отображения.

Назовем пару (x,y), X Е Rⁿ, у Е R^m, обучающим примером.

В различных практических задачах обучающими примерами могут быть:

• в задачах классификации: X — набор значений параметров, у — номер класса, которому соответствует данный набор;

• в задачах прогнозирования: X — набор значений некоторой величины за последние n замеров, у — прогнозируемое значение этой величины;

• в задачах аппроксимации: X — аргумент функции, у — значение аппрок­симируемой (приближаемой) функции в точке X;

• в задачах управления: X — входное управляющее воздействие некоторой динамической системы, у — выход системы.

Обозначим все множество обучающих пар (X,y) для данной задачи M. В практических задачах множество M состоит обычно из конечного числа пар: M = {(X¹ ,у¹)} i=i..._p.

Если в необученную сеть ввести входной сигнал X одного из обучающих примеров выборки M, то выходной сигнал у = N(X, W, B) будет отличаться от требуемого у, определенного в обучающем примере.

Обучить многослойную сеть прямого распространения — это значит най­ти такие параметры W, B, чтобы ошибка сети на всем множестве обучающих примеров была как можно меньше.

К обучению сети возможны три подхода:

• обучение на всем множестве примеров;

• одиночное предъявление обучающих примеров;

• постраничное обучение.

Обучение на всем множестве примеров

Рассмотрим более подробно метод обучения на всем множестве примеров.

Составим функцию ошибки, которая определяет степень близости вход­ных сигналов к требуемым при решении всей совокупности примеров обуча­ющей выборки:

pm

V = 2 ЕЕ (у1 - у)²’ (8)

1=1 i=1

где yi — i-я компонента вектора N(X¹, W, B).

Функция (8) представляет собой сумму ошибок по всем обучающим при­мерам.

Таким образом, обучение сети эквивалентно задаче нахождения глобаль­ного минимума функции V многих переменных.

Для многослойной сети прямого распространения, состоящей из L основ­ных слоев, где k-й слой содержит N^k нейронов, число переменных функции LL

• будет равно ^ NkNk_-1 + ^2 Nk, то есть сумме общего числа связей и об- k=1 k=1 щего числа смещений.

Для решения задачи минимизации V ^ min может быть использован весь арсенал известных методов оптимизации:

• алгоритмы локальной оптимизации с вычислением частных производ­ных первого порядка;

• алгоритмы локальной оптимизации с вычислением частных производ­ных первого и второго порядков;

• стохастические алгоритмы;

• методы глобальной оптимизации.

Алгоритм обратного распространения ошибки

Наиболее используемым алгоритмом обучения многослойной сети прямо­го распространения является алгоритм обратного распространения ошибки (back propagation). Это рекурсивный алгоритм, который сначала применяет­ся к выходным нейронам сети, а затем проходит сеть в обратном направлении до первого слоя. В его основе лежит градиентный метод поиска минимума функции многих переменных. Синаптические веса настраиваются в соответ­ствии с формулами

j + 1) = j) + £ ^£ дМ.' (t)yi^fc-^1]''(t);

l=1 г = ¹...^{, N}k—1^{; j} = ¹...^{, N}k^{; k} = ^ ^{L — 1}...^{, 2;}

^p

^(t + ¹⁾ = ^(t) + ^££ ^д1](t)xi; ^г = ^1,... ^,No; ^j = ¹... ^,N1; '=1

j.' = (yj — yj^L’ .')/.'); j = 1,..., Nl; Nl = m;

Nfc₊i

дМ.' = £ д!^к+1].'w.jk|^+1]/'(sj^k].'); j = 1,..., Nk; k = L — 1, L — 2,..., 1;

i=1

bj^k] (t + 1) = + £ £ д»'(t); j = 1,..., Nk; k = L, L — 1,..., 1. '=1

Индекс l сверху означает, что данная величина вычислена для l-го обу­чающего примера.

Обучение на всем множестве примеров связано с определенными трудно­стями:

• все примеры могут не уместиться в оперативной памяти;

• сразу всех примеров может и не быть;

• есть шанс попадания в локальный минимум.

Поэтому полезно предварительное обучение на меньшем количестве приме­ров.

Метод одиночного предъявления примеров

Суть этого подхода состоит в том, что после предъявления обучающего при­мера параметры сети модифицируются так, чтобы улучшить решение одно­го примера. С этой целью используются формулы метода back propagation с числом обучающих примеров равным единице, при этом они примут вид

w[(t + 1) = wij(t) + гД[^к| (%Г^-1|(г); ⁱ = ^ . . . ^{, N}k-1^{; j} = ^1, . . . ^{, N}k^{; k} = ^{L, L} — ~^1, . . . ^{, 2;} wjj(t + 1) = wj¹ (t) + гД^^1](t)X_!; i = 1,..., No; j = 1,..., N1; Д'⁴ = (yj — yj^L)f'(sj^L|); j = 1,..., Nl; Nl = m;

^Nk+1

д[_Ч = ^ дц-_Чwjk+Чf'(sW); j = 1,..., Nk; k = L — 1, L — 2,..., 1;

i=1

b[^](t + 1) = bj^k|(t) + гД[^к| (t); j = 1,..., Nk; k = L, L — 1,..., 1.

Недостатками этого подхода являются:

• обучение происходит слишком медленно, так как величину г необходимо брать очень малой, иначе при обучении будет теряться навык к уже пройденным примерам;

• неустойчивость сходимости.

Постраничное обучение

При постраничном методе сети предъявляются для обучения примеры се­риями, то есть страницами. Страница — серия примеров, предъявляемая се­ти для обучения. Модификация параметров сети осуществляется исходя из всех примеров страницы. Первую страницу рекомендуется формировать из опорных примеров, характеризующих особенности функции, которую долж­на будет реализовать сеть (например, если сеть обучают классифицировать образы, то в первую страницу рекомендуется включить наиболее ярких пред­ставителей каждого класса).

В ходе обучения объем страницы и разнообразие примеров на ней можно увеличить (так как после начального образования появляется возможность для быстрого освоения все больших страниц).

Кроме того, важно, чтобы каждая страница была достаточно разнооб­разной, и на ней присутствовали представители разных классов

Для каждой страницы применяются формулы back propagation с той лишь разницей, что суммирование идет только по тем примерам, которые входят в данную страницу.

7. Использование многослойной сети прямого

распространения для решения задач аппроксимации

Фундаментальным фактом, лежащим в основе использования многослойной сети прямого распространения при решении многих практических задач, яв­ляется способность такой сети аппроксимировать любое непрерывное отоб­ражение.

Постановка задачи

Пусть R^m означает m-мерное евклидово пространство с расстоянием p_m(x, y) между векторами x = (x₁,..., x_m) и y = (y₁,..., y_m), задаваемое по формуле

m

В частности, при m = 1 будет p(x,y) = |x — y|.

Определение 1. Пусть заданы два отображения f : Q ^ R^m и g :

Q ^ R^m, где Q есть ограниченное замкнутое подмножество простран­ства Rⁿ. Говорят, что функция g аппроксимирует (приближает) функ­цию f с ошибкой (точностью) е > 0 на множестве Q С Rⁿ, если

Pm^{(f (x),}g^(x)) < ^е

для всех x Е Q.

Определение 2. Пусть Q есть ограниченное замкнутое подмножество пространства Rⁿ. Обозначим Cq^r™ множество всех непрерывных отоб­ражений из Q в R^m. Пусть G — некоторое множество отображений, опре­деленных в Q, со значениями в R^m. Говорят, что множество G плотно в множестве Cq^r™, если для любого f Е Cq^r™ и любого е > 0 существует g Е G, которое аппроксимирует f с заданной точностью е на Q.

В качестве G (то есть множества, всюду плотного в Cq^r™ ), желательно брать такое, элементы которого бы имели простую структуру и допускали легкую реализацию на ЭВМ. В качестве G можно взять множество отобра­жений, реализуемых многослойными сетями прямого распространения.

Теорема 2 (теорема о полноте). Пусть Q есть ограниченное замкнутое подмножество пространства Rⁿ. Множество всех отображений, осущест­вляемых многослойными сетями прямого распространения с n входами, m выходами, является плотным в Cq^r™ тогда и только тогда, когда функ­ция активации а является непрерывной и не является многочленом.

Таким образом, нейронные сети являются универсальными структурами, позволяющими реализовать любой вычислительный алгоритм. Для пред­ставления многомерных функций многих переменных может быть исполь­зована однородная двухслойная нейронная сеть с сигмоидальными переда­точными функциями.

m

N

+ 1 I (n + m + 1) + m,

Для оценки числа нейронов в скрытых слоях однородных нейронных се­тей можно воспользоваться формулой для оценки необходимого числа синап­тических весов L_w в многослойной сети с сигмоидальными передаточными функциями:

где n — размерность входного сигнала, m — размерность выходного сигнала, N — число элементов обучающей выборки.

8. Использование нейронных сетей

для решения задач прогнозирования

Прогнозирование экономических процессов

Задача прогнозирования состоит в вычислении и предсказании некоторых деталей будущего. Затем эта информация используется менеджерами для принятия стратегического решения. Для создания прогноза обычно исполь­зуются данные исторического тренда, а также статистические методы или модели линейного программирования. Существуют:

• качественные методы прогноза, например, мнение экспертов (Delphi me­thod), или отчеты об исследовании потребительских предпочтений;

• методы анализа временных рядов (Time Series Analysis Methods), напри­мер, метод изменчивого среднего (moving average), метод Бокса —Джен­кинса;

• причинные методы (causal methods), например, анализ статистических требований (Statistical demand analysis), или экономические модели.

Задача прогнозирования продаж

Прогнозирование продаж играет видную роль в системах принятия реше­ний. Эффективное и заблаговременное предсказание продаж может помочь ЛПР вычислить стоимость продукции, материальных затрат, и даже опре­делить цену продаж. Большинство методов, применяемых для предсказания продаж, используют те или иные факторы или данные временных рядов. Однако зависимость между этими факторами или данными временных ря­дов (независимые переменные) и величиной продаж (зависимая переменная) всегда слишком сложная. Получение результата посредством вышеуказан­ного подхода слишком трудоемко. Поэтому многие ЛПР используют свою интуицию, а не подходы, связанные с построением моделей.

Задача прогнозирования курса акций

В настоящее время имеется много методов для определения тенденции курса акций. В соответствие со своими специфическими свойствами они могут быть классифицированы следующим образом.

1. Технический анализ — проводится анализ тенденции курс акции в соот­ветствие со стоимостью и транзакциями в прошлом. Основой техниче­ского анализа является математическая статистика и теория математи­ческого прогнозирования. При этом могут быть использованы:

• линейная регрессионная модель Y = f (xi,... ,x_n) для определения прогноза, где Y — прогнозируемая величина, x_i,...,x_n — независи­мые переменные (факторы), f — линейная функция;

• нелинейная регрессионная модель, f — нелинейная функция, (при­мер—функция Кобба—Дугласа Y = XK^aL^i-a);

• авторегрессионная модель (при анализе данных временных рядов);

• другие методы прогнозирования случайных процессов.

2. Элементарный анализ — анализ внутренней информации, появляющейся на рынке. Например, формы финансовых отчетов, отчеты о прибылях и убытках, экономические статьи и т.д. Примером может служить па­дение курса акций Microsoft после решения суда о признании компании виновной в нарушении антимонопольного законодательства.

3. Информационный анализ — в его основе лежит анализ финансовой и ин­дустриальной политики правительства, выход государства на рынок ак­ций, война и т.п.

Следует отметить, что имеется много примеров как успешного, так и неудачного применения этих трех подходов к прогнозированию тенденции курса акций.

Отметим также, что в основе современного подхода к решению задачи прогнозирования лежит концепция детерминизма. Каждый из трех выше­упомянутых методов основан на этой концепции. Основная ее идея состоит в том, что для фиксированных начальных условий будущее является строго определенным, детерминированным. И даже если начальные условия имеют небольшую ошибку, будущее может быть определено приближенно.

Вместе с тем тенденция движения курса акций связана с потребностью акций со стороны населения. Это как раз та причина, по которой прогнозиро­вание тенденции движения курса акций есть чрезвычайно трудная проблема.

Кроме того, современная экономическая наука утверждает, что прогноз рынка принципиально невозможен.

Действительно, классическая модель Эрроу — Дебре утверждает, что эко­номическая система имеет конечное число точек равновесия, причем в окрест­ности любого устойчивого равновесия поведение системы слабо зависит от ее истории. Современная модель Эрроу — Дебре описывает взаимодействие многих рынков. В модель включены неопределенность и рынок ценных бу­маг. Доказано, что для такой модели число равновесий не просто бесконечно, но и континуально. Динамика такой системы принципиально не прогнозиру­ема и существенно зависит от характера пусть даже небольших внешних воздействий.

Многослойная сеть прямого распространения как возможный инструмент прогноза

Отметим причины, по которым многослойная сеть прямого распространения может быть применена для решения задач прогноза.

1. Такая сеть обучается на примерах и «добывает» необходимую функцио­нальную зависимость между зависимыми и независимыми переменными, даже если эта зависимость неизвестна и трудна для описания. Поэтому некоторые исследователи трактуют FANN как один из многопеременных нелинейных непараметрических статистических методов.

2. Многослойная сеть прямого распространения способна к обобщению. По­сле обучения сеть может делать корректное заключение для примеров, не входящих в обобщающую выборку, даже если данные имеют «шум».

3. Многослойная сеть прямого распространения — универсальный аппрок- симатор.

4. Многослойная сеть прямого распространения — нелинейна, в то время как большинство традиционных методов прогноза предполагают, что рассматриваемые временные ряды порождены линейными процессами. На самом деле процессы реального мира часто нелинейные.

Существует два подхода к применению многослойной сети прямого рас­пространения при решении задач прогнозирования.

1. Предсказание на основе независимых переменных-причин. В этом слу­чае вход сети — независимые предикаторные переменные. Функциональ­ная зависимость может быть представлена в виде у = f (x₁,... ,x_p), где X₁, . . . , X_p есть p независимых переменных, а у является зависимой пере­менной. В этом случае многослойная сеть прямого распространения есть функциональный эквивалент нелинейной регрессионной модели.

2. Экстраполяция, или задача прогнозирования временных рядов. Вход се­ти есть предыдущие наблюдения рядов данных, а выход — будущее (про­гнозируемое) значение. Сеть представляет следующую функциональную зависимость:

^yt+1 = ^{f (y}t, ^yt-1,..., ^yt-p⁾,

где y_t — значение наблюдаемой величины в момент t.

В этом случае многослойная сеть прямого распространения есть эквива­лент нелинейной авторегрессионой модели для задач прогнозирования на основе временных рядов.

Обучающий пример состоит из конечного набора предыдущих значений временного ряда. Предположим, мы имеем N значений у₁,... ,y_n в обу­чающем множестве и мы строим одношаговый прогноз. Тогда, используя FANN с n входами, мы получаем N — n обучающих примеров. Первый из них состоит из у₁,..., y_n и y_n+1 — требуемый (желаемый) выход. Второй будет содержать у₂,..., y_n+1 и y_n+₂ — желаемый выход. Наконец, послед­ний обучающий пример: y_N—n, y_N—n+₁,..., y_N—1 — на входе и y_N — цель.

Процесс обучения сети состоит в минимизации функций ошибки

1. ^N

• = 2 S ⁽У^{г - ai)2}’

i=n+1

где ai — действительный выход сети для i-го обучающего примера.

Выводы по использованию нейронных сетей для решения различных задач прогнозирования

Оценке возможностей нейронных сетей прямого распространения для реше­ния задач прогнозирования на основе временных рядов посвящено большое количество исследований. Однако их заключения часто противоречат друг другу. Часть из них заключают, что нейронные сетей прямого распростране­ния лучше, чем общепринятые методы, другая часть утверждает обратное. При сравнении нейронных сетей прямого распространения и модели Бокса- Дженкинса (при этом использовались данные о графике пассажирских авиа­перевозок, данные об объемах продаж в США автомобилей фирм США и автомобилей зарубежных производителей) эксперты пришли к выводу, что модель Бокса — Дженкинса дает лучший краткосрочный прогноз, в то время как модель на основе нейронных сетей предпочтительнее при долгосрочном прогнозе.

Вслед за успешным применением нейронных сетей прямого распростране­ния в научных работах практически все системы для интеллектуального ана­лиза данных используют нейронные сети в качестве инструмента прогноза.