Одномерное частотное распределение

ОЧР имеёт вид таблицы, содержащие следующие данные:

- первый столбец: значения изучаемой переменной;

- второй: абсолютная частота;

- третий: относительная частота в процентах;

- четвертый: рассчитывается только для количественных признаков и порядковых шкал, и содержит накопленную частоту.

Таблица ОЧР строится на основании данных матрицы «объект-признак».

Абсолютная частота – f_i. Относительная частота (в процентах). В сумме – 100%. f_i(%) = f_i/n* 100%. Замечание: теории статистического вывода вместо относительной частоты процентов используется относительная частота в долях от 1. Когда мы строим таблицу одномерного распределения для количественного признака, мы обязательно должны упорядочить значения признака по возрастанию. Накопленные частоты: абсолютные и относительные в процентах, возрастающие и убывающие – F_i(%). Наиболее часто исследователи пользуются возрастающие накопленной частотой в процентах. Если рассчитываем возрастающую накопленную частоту, начинаем с частоты, соответствующей первому значению признака. Накопленные частоты могут использоваться при ответе на вопрос, например: «Каков процент респондентов, возраст которых меньше либо равен 35 годам?». Одномерное частотное распределение количественных признаков называется вариационным рядом.

Возраст	fi	fi(%)	Fi(%)
16	1	2,4	2,4
17	15	36,5	38,9
18	19	46,3	85,2
19	3	7,3	92,5
20	2	4,8	97,3
21	1	2,4	99,7
	n = 41

Группировки количественных признаков в интервалы. Количественные признаки, имеющие достаточно большие разбросы значений или длинный/большой вариационный ряд, принято группировать в интервалы. Проводя группировку, исследователю необходимо решить ряд задач. Необходимо определить:

1) сколько интервалов будет содержать данная группировка;

2) интервалы одинаковой или разной длины;

3) каким образом будут определены границы интервалов.

Необходимо для того, чтобы всевозможные значения признаков имели свое место в группировке, а также чтобы каждое значение признака входило только в один интервал.

Наиболее важным является определение границ интервалов. Для границы интервалов важно, чтобы:

1) границы не пересекались;

2) не терялись значения непрерывных признаков.

Если возникает ситуация, когда теряются промежуточные значения непрерывного признака, необходимо при построении интервалов указывать пресекающиеся границы и одновременно отмечать, каким образом эти границы закрыты, то есть, если границы закрыты сверху, то пересекающееся значение попадает в первый (верхний) интервал; если снизу или слева, попадает в нижний или следующий интервал. Интервалы с пересекающимися границами строятся на этапе анализа данных. Если группировку интервалов мы хотим предоставить респондентам в качестве инструментария, пользоваться пересекающимися границами нельзя. В этом случае мы должны четко разграничивать значения переменных по интервалу. Если интервалы закрыты сверху, доход, равный 500 000, попадает в 1-ый интервал (от 100 000 до 500 000).

Существует три вида группировки интервалов:

1) типологическая;

2) аналитическая;

3) процентивная.

1) При построении типологической группировки не применяются какие-либо конкретные методики, а производится разбиение на интервалы в соответствии с задачами исследования и теоретическим представлением о том, как изменяется отношение к предмету исследования в зависимости от значения признака. То есть, исследователь сам определяет количество интервалов, длину интервалов, а также будут ли границы интервалов пересекающимися или не пересекающимися.

Основная задача исследователя: после группировки суметь теоретически обосновать каждый полученный интервал.

2) Это разбиение на заданное число интервалов равной длины. Для того чтобы построить аналитическую группировку, нужно померить интервалы.

1. D = x_max – x_min.

2. d/7 < l < d/6.

Количество интервалов равны 6 или 7, если объём выборочной совокупности не превышает 100 наблюдений. Если объём выборки превышает 100 и d (размах вариаций) имеет достаточно большое значение, рассматривают 12- 15 интервалов: d/15 < l < d/12 (государственная статистика). Длина интервала l всегда целое число, поэтому, если в определенных границах не содержится целого числа, берем (целое) l, ближайшее к дробному числу. Границы всегда пересекающиеся.

3) Это разбиение на заданное число интервалов с заданным процентным объектом из выборки.

В процентильной группировке длины интервалов разные, а частоты внутри каждого интервала одинаковые. При построении процентивной группировки вводится понятия квантиля (= процентиля). Квантиль (значение признака) - x_p, где p показывает, какая доля объектов из выборки имеет значение признака, меньшее квантиля.

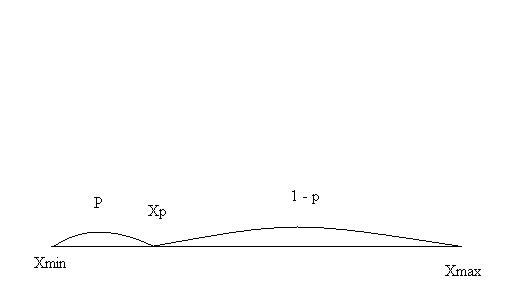
Существует несколько разновидностей ПГ:

1) Наиболее используемая – квартильная группировка – группировка, состоящая из 4 интервалов по 25% объектов из выборки:

x_min, x_0,25 , x_0,5, x_max;

2) терцильная – 3 интервала по 33,3% из выборки:

x_min, x_0,33, x_0,66, x_max;

3) квинтильная – 5 интервалов по 20%:

x_min, x_0,2, x_0,4, x_0,8, x_max;

4) децильная - 10 интервалов по 10%:

x_min, x_0,1…

Для того чтобы построить ПГ, пользуются возрастающей накопленной частотой.

1. Если ПГ строить по вариационному ряду, то соответствующие квантили определяются по возрастающей накопленной частоте, равной либо впервые превысившей значение p*100%. Данный способ определение границы ПГ является приблизительным.

2. Если необходимо определить точное значение квантилей, необходимо в качестве основы использовать аналитическую группировку и специальную формулу: .

Х₀ – левая граница интервала, в котором содержится искомый квантиль.

l – длина интервала

p * 100% – процент объектов из выборки, соответствующий квантилю.

F₀ – накопленная частота, соответствующая предшествующему искомому интервалу.

f_p – частота в процентах, соответствующая интервалу, содержащему квантиль.

Пример:

	fi	fi(%)	Fi(%)	F*
10-20	17	41,5	41,5	99,6
20-30	5	12,1	53,6	58,1
30-40	5	12,1	65,7	4,6
40-50	8	19,5	85,2	33,9
50-60	11	9,6	94,8	14,4
60-70	1	2,4	97,2	4,8
70-80	1	2,4	99,6	2,4

d < 75 -10 = 35

65/7 < l < 65/6

9,3 < l < 10,8

l = 10

x_min = 10

x_0,25 = 20

x_0,5 = 30

x_0,75 = 45

x_max = 75

	Fi(%)
10-20	25
20-30	25
30-45	25
45-75	25
	100%

x_min = 10

x_0,25 = = 16

x_0,5 =

x_0,75 = = 44,7

x_max = 80

	Fi(%)
10-16	25
16-26,7	25
26,7-44,7	25
44,7-80	25
	100%