13 Основные теоремы и применения дифференциального исчисления

13.1 Теоремы о среднем значении

Чтобы применять производную для изучения функций, нам будут нужны несколько теорем. Самая простая из них (теорема 1 ниже) содержит необходимое условие экстремума. Дадим точное определение этого понятия.

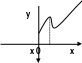Пусть функция f(x) определена в окрестности точки x₀. Говорят, что в точке х₀ функция имеет локальный максимум, если существует окрестность U_(x₀) такая, что f(x₀)  f(x) для любой точки xU_(x₀). Слово «локальный» подчёркивает, что f(x₀) является наибольшим среди значений функции лишь в точках, близких к x₀ (в точках некоторой окрестности).

Аналогично даётся определение локального минимума: x₀ – точка локального минимума  U_(x₀): xU_(x₀) f(x₀) f(x). Обратите внимание: неравенства в этих определениях нестрогие. Так удобнее, хотя и приходится считать, например, что постоянная функция в каждой точке имеет и максимум, и минимум. Понятие «экстремум»  обобщающее: это или локальный максимум, или локальный минимум.

Теорема 1 (теорема Ферма). Если х₀  точка экстремума функции f(x) и существует производная f ′(x₀), то f ′(x₀)  0.

Доказательство. Пусть, для определённости, х₀ – точка локального максимума. Дадим аргументу приращение х. Заметим, что f  f(x₀+x)f(x₀)  0, по определению максимума. Значит, если x > 0, т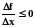о , а если x < 0, то 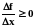. Поэтому

,

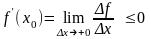Значит f (x₀)  0, что и требовалось доказать.

Замечание. Условие f (x₀)  0 не является достаточным для экстремума: функция f(x)  x³ имеет в точке х  0 нулевую производную:

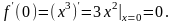
Однако ни максимума, ни минимума в этой точке нет.

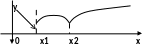С другой стороны, локальный экстремум может достигаться в точках, где функция не дифференцируема или даже разрывна. На рисунке x₁, x₂ – точки локальных экстремумов

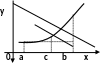
Теорема 2 (теорема Ролля). Пусть f(x) непрерывна на [a, b] и дифференцируема на (a, b) (во всех внутренних точках). Если f(a)  f(b), то существует c(a, b): f (c)  0. Доказательство. Пусть M, m  наибольшее и наименьшее значения f(x) на [a, b]. Как мы знаем (теорема 6 из 11.2), эти значения достигаются в некоторых точках. Если и m, и М достигаются на концах отрезка, то по условию m  M, т.е. функция постоянна. Тогда её производная равна 0 в любой точке. Если же хотя бы одно из значений m, M достигается во внутренней точке c, то в этой точке f(x) имеет, очевидно, экстремум. По теореме 1 f (c)  0.

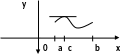Замечание. На геометрическом языке теорема Ролля утверждает, что при указанных у

словиях касательная к графику функции в некоторых точках параллельна оси ОХ.

Приведём графические примеры, показывающие необходимость каждого из условий теоремы Ролля: если одно из них нарушено, то производная может не обращаться в нуль ни в одной точке.

Теорема 3 (теорема Коши). Пусть функции f(x), g(x) непрерывны на [a, b], дифференцируемы на (a, b), причём g′(x)  0 (x  (a, b)). Тогда c  (a, b):

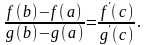
Доказательство. Рассмотрим функцию F(x)  f(x)  g(x), где число  подберём так, чтобы к F(x) можно было применить теорему Ролля. Непрерывность и дифференцируемость, конечно, имеются при любом . Чтобы выполнялось F(a)  F(b) нужно: f(a)–g(a)  f(b)g(b), т.е. 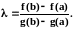(Заметим, что g(b)  g(a)  0, так как иначе, по теореме Ролля, g′(x)  0 в некоторой точке).

Применяем к F(x) теорему Ролля: с: F′(c)  0. Значит f′(c)  g′(c)  f ′(c)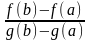 g′(c)  0. Отсюда получаем: 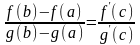, что и требовалось.

Теорема 4 (теорема Лагранжа). Если f(x) непрерывна на [a, b], дифференцируема на (a, b), то c  (a, b): f(b)  f(a)  f ′(c)(b  a).

Доказательство. Применим теорему Коши для случая, когда g(x)  x. Так как g′(x)  1, то получим требуемое соотношение.

Замечание. Имеется простая геометрическая интерпретация теоремы Лагранжа. Величина 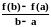равна тангенсу угла наклона секущей, проведённой через точки (a, f(a)), (b, f(b)). Так как f (c)  тангенс угла наклона касательной, то теорема Лагранжа фактически утверждает: при указанных условиях всегда найдётся точка c  (a, b), в которой касательная параллельна секущей.

Следствие. Если f(x) дифференцируема на (a, b), причём f ′(x)  0 (x(a, b)), то f(x)  C  постоянная функция.

Доказательство. Возьмём любые x₁, x₂  (a, b), x₁ < x₂. По теореме Лагранжа

c  (x₁, x₂): f(x₂)  f (x₁)  f ′(c) (x₂  x₁).

Но f ′(c)  0. Поэтому f(x₁)  f(x₂), значения функции во всех точках одинаковы.

Заметим, что теорема Лагранжа  частный случай теоремы Коши, а теорема Ролля – частный случай теоремы Лагранжа. Во всех этих теоремах речь идёт о существовании некоторого числа c  (a, b), точное значение которого остаётся неизвестным. Теоремы Ролля, Лагранжа, Коши обычно называют теоремами о среднем значении.