Задачи с решениями
Пользуясь определением, найти производную функции
.
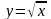Чему равно значение y(9)
?
Решение. Найдём сначала производную в произвольной точке x, затем в полученную формулу подставим x 9. Пусть x – приращение x. Тогда
.
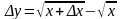Составим
отношение
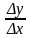и перейдём к пределу при x
0:
.
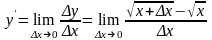Чтобы раскрыть
неопределённость, умножим числитель и
знаменатель на
:
.
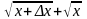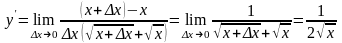Производная
найдена. Её значение
.
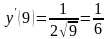Найти производную функции
.
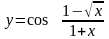Решение. Последнее действие – вычисление косинуса. Поэтому, используя табличную производную косинуса, получим:
.
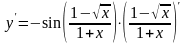Теперь требуется найти производную от более простого выражения. Последнее действие в нём – деление. Применяем правило дифференцирования частного :
.
Осталось
вычислить довольно простые производные.
Учитывая, что 1
0 (производная постоянной есть 0
), x
1,
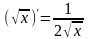( это частные случаи табличной формулы
(x)
x–1
), используя правила дифференцирования
суммы и разности, получаем:
,
.
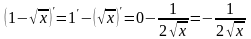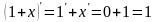Окончательно
.
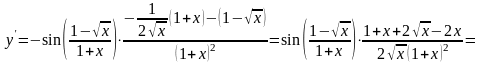
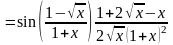Последние преобразования сделаны для того, чтобы записать ответ в более простой форме.
Найти производную функции
.
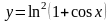Решение. Действуем так же, как в предыдущей задаче, но без подробных комментариев:
.
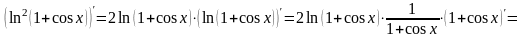
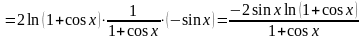Найти
,
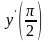если
.
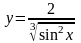Решение. Хотя последнее действие – деление, нет смысла применять правило дифференцирования частного. Проще записать выражение в виде степени:
.
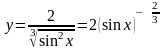Теперь
легко находим:
.
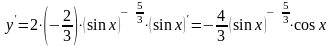Так
как
,
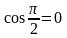то
.
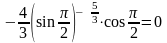Найти производную функции
.
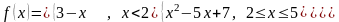Построить графики функции и её производной.
Решение. Во всех точках, кроме x 2 и x 5, функция легко дифференцируется:
.
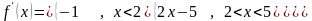В точке x
2 левая производная f
(2–0)
–1, правая производная f
(2+0)
.
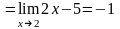Следовательно, в точке x
2 функция дифференцируема
и f (2)
–1.
В точке x
5 левая производная
,
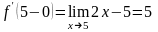правая производная f
(5
+ 0)
–1. Значит, f
(5)
не существует. Итак,
,
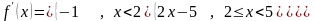f (5)
не существует.
Построим графики:
С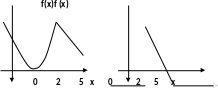
трелки
на концах линий, как обычно, означают
то, что концевая точка им не принадлежит.
Является ли функция
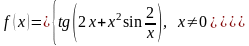
дифференцируемой в точке x 0 ? Если является, то найти f (0).
Решение. Проверим прежде всего, что f(x) непрерывна в 0:
.
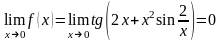Последнее
равенство следует из того, что
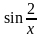– ограниченная функция, значит
– бесконечно малая, а поэтому и
.
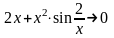Вычислим производную по определению:
.
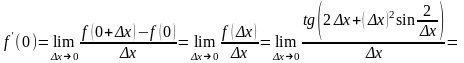
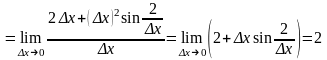При вычислении предела воспользовались тем, что tg(x) ~ (x), если (x) 0. Итак, функция в x 0 дифференцируема и f (0) 2.
Замечание. Если в определении
f(x)
заменить
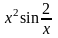на
,
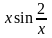то функция не будет дифференцируемой
в точке x
0, так как
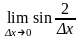не существует.
Для функции f(x) (1 + x2)arctgx найти f (1).
Решение. Последнее действие – умножение, поэтому применяем правило дифференцирования произведения:
,
,
.
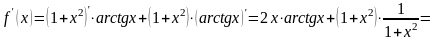
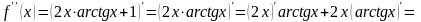
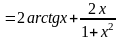Функция y y(x) задана неявно: 4x3 + 3xy + y3 0. Найти y(1).
Решение. Найдём значение y(1), подставляя x 1 в уравнение: 4 + 3y + y3 0. Легко заметить, что y –1 – корень. Так как 4 + 3y + y3 (y + 1)(y2 – y + 4), то других действительных корней нет. Итак, y(1) –1.
Дифференцируем равенство, задающее функцию, по x, считая y y(x):
12x2 + 3y +3xy + 3y2y 0,
Разделим для упрощения на 3: 4x2 + y + xy + y2y 0. Подставляем сюда x 1, y –1:
4 + (–1) +(1)y + (–1)2y 0.
Отсюда получаем: y(1) –1,5.
Дифференцируем второй раз:
8x + y +y +xy +2y(y)2 +y2y 0.
Подставляем сюда x 1, y(1) –1, y(1) –1,5:
8 + 2(–1,5) +y(1) +2(–1)(–1,5)2 +(–1)2y(1) 0,
8 – 3 – 22,25 + 2y(1) 0,
.
.
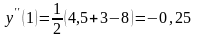Найти уравнение касательной к линии
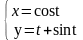, t(0
, ),
проведённой
в точке с абсциссой x 0,5.
Решение. Указанной точке
соответствует значение параметра
:
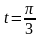cost
0,5, t
(0, )
.
Ордината этой точки равна
.
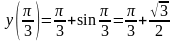Найдём угловой коэффициент касательной:
.
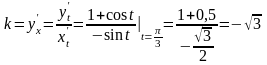Уравнение прямой, проходящей через (x0, y0) с угловым коэффициентом k имеет вид:
y – y0 k(x – x0).
Значит, уравнение касательной:
,
.
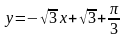В какой точке касательная к графику функции y lnx параллельна прямой
y 2x – 3 ?
Решение. Угловой коэффициент данной прямой k 2. Значит, мы должны найти точку, в которой угловой коэффициент касательной (т. е. производная) равен 2:
.
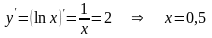Найти касательные к параболе y x2 – 4, проходящие через точку (2, –1).
Решение. Запишем уравнение касательной к данной параболе, проведённой в точке кривой (x0, y0):
y – y0 y (x0)(x – x0).
Так как
,
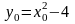y(x0)
2x0, то
уравнение касательной принимает вид:
.
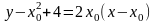Нам нужно узнать: при каком x0 эта прямая пройдёт через точку (2, –1) ? Подставим x 2, y –1 и найдём такие x0:
,
,
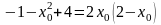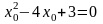x0 1, x0 3.
Для точки x0 1 касательная y + 3 2(x – 1), или y 2x – 5. Для точки x0 3 касательная y – 6(x – 3), или y 6x – 13.
Найти дифференциал функции
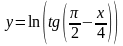в точке x
.
Решение. Дифференциал функции в точке x0 находим по формуле:
dy y(x0)dx.
Сначала найдём производную:
.
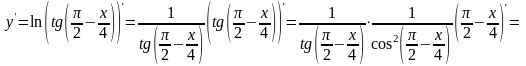
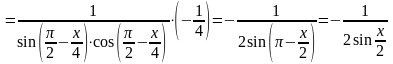Здесь, чтобы упростить выражение, мы использовали тригонометрические формулы:
sin2 2sincos, sin( – ) sin.
Общая формула для дифференциала получена:
.
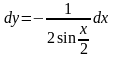Далее:
.
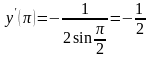Значит, в точке x
дифференциал равен
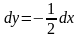(или dy
,
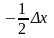это то же самое).
Вычислить приближённо
.
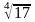Решение. Рассмотрим функцию
.
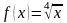Её значение в точке x
16 вычисляется легко:
.
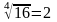Значит, нам достаточно найти приращение
функции:
f f(17) – f(16) f(x0 + x) – f(x0).
Воспользуемся тем, что f df и вычислим значение дифференциала функции f(x) в точке x0 16, соответствующее приращению x 17 – 16 1:
.
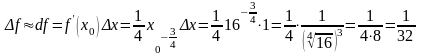Значит
.
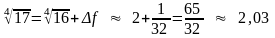