X  u  cosx  V  lnu  y  v2  (ln cosx)2.

Каждая стрелка – основная элементарная функция, их производные есть в таблице:

.

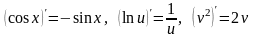По теореме 6, производная суперпозиции равна:

.

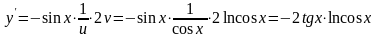Если составляющих функций много, возможно встречаются и арифметические операции, то полезно начать дифференцирование с последнего действия. Точнее, если y  f(u(x)), то по теореме 6 : y  f (u(x))u(x), и далее требуется дифференцировать более простую функцию u(x).

Пример 15. Найти производную функции .

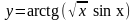Решение. Последнее действие – вычисление арктангенса. По таблице находим: . Поэтому

.

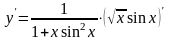Теперь требуется найти более простую производную 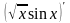. Последнее действие – умножение, поэтому применяем формулу для производной произведения (см. теорему 3):

.

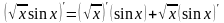Заметим, что , поэтому 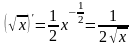. Окончательно получаем:

.

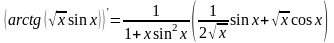Пример 16 . Найти производную .

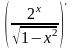Решение. Последнее действие – деление, поэтому применяем формулу для производной частного (теорема 4):

.

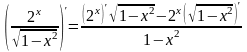Производная 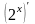есть в таблице, а чтобы найти нужно применить теорему о производной сложной функции. Последнее действие – извлечение корня:

.

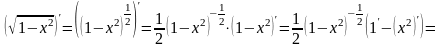
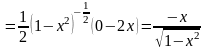Подставляя найденные производные, получим:

.

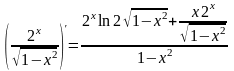12.2.5. Другие случаи вычисления производных. Функция может быть задана не только явной формулой, выражающей зависимость y от x, но и другими способами. Рассмотрим случай параметрического задания функции :

x  (t) , y  (t), t  [, ].

Напомним: здесь x – независимая переменная, а y есть функция от x: y  y(x). Однако зависимость y от x задана не непосредственно, а через параметр. Как дифференцировать такую функцию? Конечно, легко найти производные функций (t) и (t):

x_t   (t) , y_t  (t) .

(Здесь индекс t означает, что мы рассматриваем функции от переменной t и вычисляем производные по этой переменной). Однако нам нужно вычислить производную .

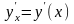Пусть для x  (t) существует обратная функция t  ^–1(x). Тогда нашу функцию можно выразить явно через x:

y(x)  (^–1 (x)).

Найдем её производную, используя теоремы о дифференцировании сложной функции и обратной функции:

.

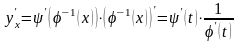В этой формуле производная 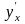снова выражена через параметр t. Чтобы установить её связь с переменной x, нужно использовать связь x и t: x  (t). Таким образом, если функция задана параметрически, то и её производная задана параметрически.

Функция: 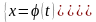. Её производная: .

Пример 17. Найти производную функции 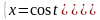. Вычислить значение производной в точке .

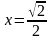Решение. По формуле, полученной выше, производная имеет параметрическое задание:

.

Точка соответствует значению параметра 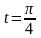. Значит, .

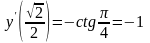Замечание. Не имеет смысла выводить специальную формулу для производной второго порядка. Указанный метод можно применить к функции столько раз, сколько потребуется.

Пример 18. Найти производную второго порядка от функции y  y(x), заданной параметрически:

.

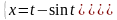Решение. Так или 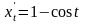, , 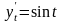то первая производная данной функции имеет вид:

.

Аналогично, вычислим сначала

.

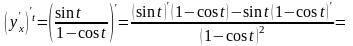
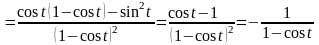Значит, вторая производная данной функции есть:

.

Теперь рассмотрим случай неявно заданной функции. При определённых условиях функция y  y(x) может быть задана равенством

F(x, y)  0.

Подставляя сюда числовое значение x и решая полученное уравнение, найдём значение функции y(x). Чтобы найти производную функции, заданной таким образом, нужно продифференцировать равенство F(x, y)  0 по x, считая при этом y функцией от x. Получим равенство, которое вместе с соотношением F(x, y)  0 неявно определяет производную y(x). Поясним сказанное на примере.

Пример 19. Найти производную функции y  y(x), заданной уравнением e^y + xy  e. Вычислить значение y(0).

Решение. Дифференцируем уравнение по x, считая y функцией от x:

.

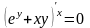Пользуемся правилами дифференцирования сложной функции и произведения:

, .

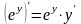Уравнение приобретает вид :

,

,

.

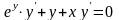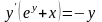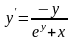Хотя мы и выразили y, явного задания не получается – в правой части есть y. Поэтому, чтобы найти y(0), сначала нужно найти y(0). Подставим x  0 в исходное уравнение:

e^y(0) + 0  e, y(0)  1.

Значит .

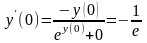В заключение раздела рассмотрим ещё один способ дифференцирования. Обычно он применяется для функций вида

f(x)  u(x)^v(x)  u^v.

Такую функцию нельзя отнести, конечно, ни к степенным, ни к показательным. Однако она является элементарной, так как её можно представить в виде:

f  u^v  e^vlnu.

Вычислим производную такой функции:

.

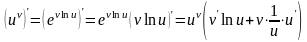Часто для вычисления (u^v) применяется другой приём, так называемое логарифмическое дифференцирование. Логарифмируем обе части равенства f  u^v :

ln f  vlnu.

Теперь вычислим производную каждой части равенства:

.

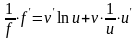Отсюда

.

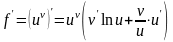Пример 20. Найти производную функции y  x^sinx.

Решение. Логарифмируем : lny  ln(x^sinx)  sinxlnx. Дифференцируем обе части равенств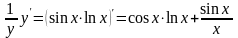а: . Отсюда:

.

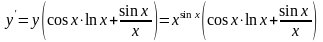Предварительное логарифмирование применяется тогда, когда производная от логарифма функции вычисляется проще, чем от самой функции. Логарифм преобразует произведение функций, частное функций в сумму или разность соответственно, а это упрощает дифференцирование.

Пример 21. Найти производную функции .

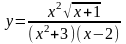Решение. Пользуясь свойствами логарифма, получим:

.

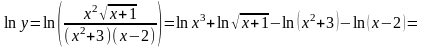
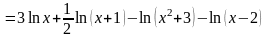Теперь легко вычислить производную:

,

.
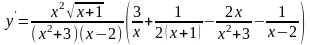