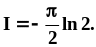16.2 Интегралы от неограниченных функций

Изучая свойства определённого интеграла Римана, мы доказали, что любая интегрируемая функция ограничена (см. 15.1). Оказывается, можно расширить понятие интеграла, можно научиться интегрировать и некоторые неограниченные функции. Причём делается это с помощью предельного перехода, очень похожим способом на только что рассмотренный способ определения интеграла по бесконечному промежутку.

П усть функция f(x) непрерывна на 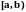и не ограничена в окрестности точки b . Например, как на рисунке. Возьмём 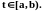Тогда на отрезке функция непрерывна, а значит существует интеграл Несобственным интегралом от функции f(x) по отрезку 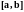называется предел

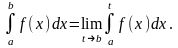
Подчеркнём: это определение нового понятия. В обычном смысле интеграл от такой функции не существует. Указанный предел тоже может не существовать или быть бесконечным. Тогда несобственный интеграл называется расходящимся. Более интересен случай, когда интеграл сходится, т. е. предел существует и конечен.

Если функция f(x) имеет особенность не в точке b, а в точке а (т.е не ограничена в её окрестности), то несобственный интеграл определяется аналогично:

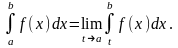
Наконец, если f(x) имеет особенность во внутренней точке с отрезка , то, по определению,

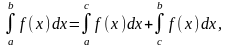
и сходимость означает сходимость каждого интеграла в правой части.

Пример 7. Вычислить

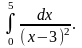
Решение. Есть опасность – не заметить, что в окрестности точки x  3 функция 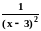не ограничена, и вычислять интеграл как обычно, по формуле Ньютона–Лейбница:

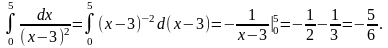
В этом примере ошибка сразу видна: интеграл от положительной функции не может быть отрицательным.

Теперь приведём правильное решение. Так как 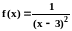не ограничена в окрестности точки x  3 , то интеграл – несобственный. По определению :

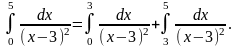
Рассмотрим, например, первое слагаемое:

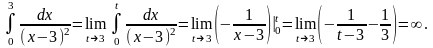
Интеграл расходится. Значит и 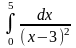расходится.

Обратим внимание на то обстоятельство, что определения двух типов несобственных интегралов очень похожи. Полностью аналогичны и свойства, которыми эти интегралы обладают. Используя эту аналогию, можно даже определение дать для обоих типов несобственных интегралов одновременно. Несобственным интегралом с особенностью в точке x  b называется предел :

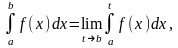
где либо 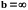, либо f(x) неограничена в окрестности b. Впрочем, обычный («собственный») интеграл Римана тоже удовлетворяет этому равенству.

Повторим формулировки наиболее важных теорем для случая интеграла с особенностью в точке b. Доказательства не приводим – они такие же, как для

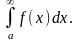
Теорема 1 (критерий Коши). сходится 

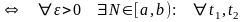
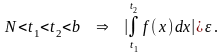
Теорема 2 (признак сравнения). Если 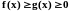в окрестности точки b, то из сходимости следует сходимость

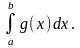
Теорема 3 (предельный признак сравнения). Если 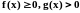в окрестности точки b, причём существует 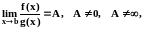то интегралы 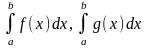или оба сходятся, или оба расходятся.

Чтобы использовать признаки сравнения для исследования сходимости несобственных интегралов, нужны уже изученные интегралы – чтобы было, с чем сравнивать. Удобно сравнивать с интегралами вида 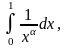где 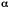– некоторое действительное число. Рассмотрим такие интегралы подробно.

Пример 8. Исследовать сходимость интегралов где

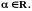
Решение. Действуем по определению:

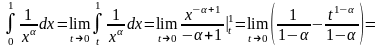
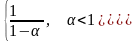
При 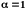нужно вычислить отдельно: 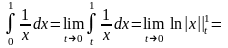. .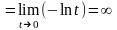 Итак, сходится

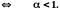
Замечание. Функция 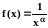непрерывна в любой точке 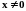. Поэтому второй предел интеграла на сходимость никак не влияет: интегралы

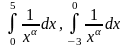сходятся или расходятся одновременно. Их сходимость связана только со свойствами функции f(x) в окрестности точки x  0 – сравните это со свойством 1 из 16.1.1. Конечно, если они сходятся, то числовые значения могут быть различными.

Пример 8 можно несколько расширить, рассматривая интеграл

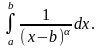
Ясно, что полученный результат справедлив и для таких интегралов:

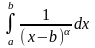сходится

Пример 9. Исследовать сходимость интеграла .

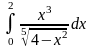Решение. Подинтегральная функция имеет особенность в точке x  2, её можно записать в виде:

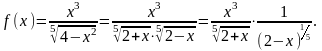
Теперь ясно, что нужно рассмотреть 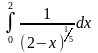(он сходится, так как 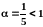) и применить предельный признак сравнения:

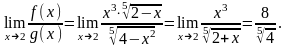
Предел отношения конечен и не равен 0, поэтому исходный интеграл также сходится.

Пример 10. Исследовать сходимость интеграла .

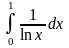Решение. Заметим, что функция 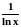не определена и в точке x  0, и в точке x 1. Однако в окрестности x  0 функция ограничена, причём 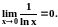Другими словами, в окрестности x  0 функция отличается от непрерывной функции лишь значением в одной точке, а значит интегрируема по Риману (в обычном, «собственном» смысле). По–другому ведёт себя 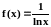окрестности x 1. Здесь она не ограничена: 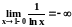. Поэтому наш интеграл – несобственный, с особенностью в точке x  1. Постараемся подобрать число  так, чтобы отношение функци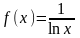й и 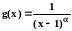имело бы при 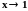конечный, не равный 0 предел:

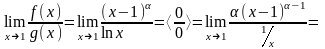
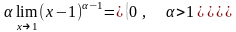
Лишь при   1 получается 1. Значит, интегралы и 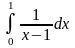ведут себя

одинаково. Второй интеграл расходится (см. пример 8 и последующее замечание), значит

расходится и интеграл

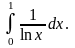
Заметим ещё, что функция принимает на интервале (0, 1) только отрицательные значения. Тем не менее, предельный признак можно применять, рассматривая функцию

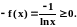
Приведём, в заключение, более сложный пример вычисления несобственного интеграла.

Пример 11. Доказать, что интеграл Эйлера сходится и вычислить его.

Решение. Особенностью интеграла является точка x  0: 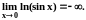Заметим, что функция 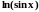принимает на интервале только отрицательные значения. Поэтому можно применять признаки сравнения, например, к интегралу 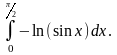Как и в предыдущем примере, попытаемся сравнить интеграл с интегралом при подходящем  (верхний предел роли не играет, можно поставить любое число). Для этого вычислим предел:

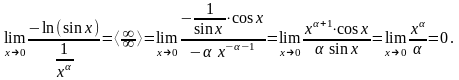
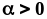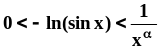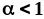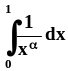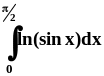(Здесь мы сначала применили правило Лопиталя, а затем воспользовались тем, что при ). Так как предел 0 при любом , то применить предельный признак сравнения не удаётся. Однако вычисление показывает, что в окрестности точки x  0 . Так как при интеграл сходится, то и сходится – по первому признаку сравнения.

Для вычисления интеграла выполним замену переменной:

.

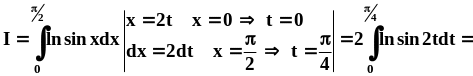
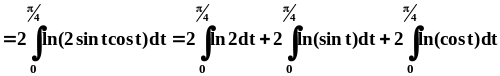Первое слагаемое вычисляется очень просто, второе будем переписывать пока без изменений, в интеграле третьего слагаемого сделаем ещё одну замену:

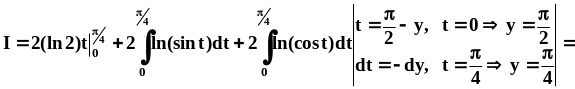
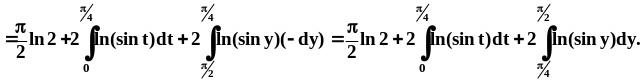Последние 2 слагаемые можно объединить в один интеграл:

.

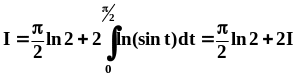Полученное соотношение позволяет нам найти I: