15.2 Интегрируемость непрерывных функций

Класс интегрируемых функций очень широк. В этом разделе мы докажем, что все непрерывные (и даже кусочно-непрерывные) функции интегрируемы. Сначала рассмотрим интегральные суммы специального вида, изучим их свойства.

Пусть функция f(x) непрерывна на [a, b]. Обозначим через B разбиение отрезка [a, b] точками x₀  a, x₁, x₂, ..., x_n-1, x_n  b. (Длины отезков [x_i-1, x_i] не обязательно одинаковы). Можно считать, что разбиение B – это и есть множество точек:

Обозначим: M_i – наибольшее значение f(x) на [x_i-1, x_i], m_i – наименьшее значение f(x) на [x_i-1, x_i]. Рассмотрим суммы:

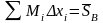– верхняя сумма Дарбу,

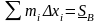– нижняя сумма Дарбу.

Так как f(x) непрерывна, то значения M_i, m_i достигаются (теорема 6, раздел 11.2) в некоторых точках. Поэтому суммы Дарбу являются частными случаями интегральных сумм.

З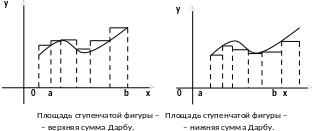 аметим, что так как то при любом выборе точек справедливо неравенство:

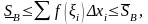
т.е. суммы Дарбу – это самая маленькая и самая большая интегральная суммы для данного разбиения. Другие свойства сумм Дарбу рассматриваются в леммах.

Лемма 1. При добавлении точек деления (т.е. при измельчении разбиения) верхняя сумма Дарбу может лишь уменьшиться, а нижняя – может лишь возрасти.

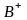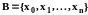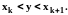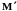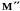Доказательство. Пусть разбиение получено из разбиения добавлением одной точки y, причём Как и выше, обозначим M_i – наибольшее значение f(x) на [x_i-1, x_i]. В разбиении появилось 2 новых отрезка. Обозначим – наибольшее значение f(x) на отрезке [x_k, y], – наибольшее значение f(x) на [y, x_k+1]. Тогда

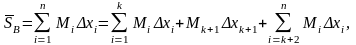
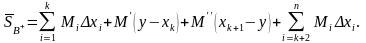
Вычтем из 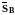и воспользуемся тем, что

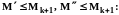
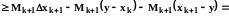
Следовательно, 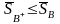. Аналогично доказывается, что

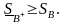
Лемма 2. Для любых разбиений B₁, B₂ отрезка [a, b]

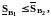
т.е. любая нижняя сумма Дарбу меньше любой верхней.

Доказательство. Рассмотрим разбиение 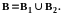Оно образовано всеми точками B₁ и B₂ и поэтому мельче, чем B₁ и B₂. Используя лемму 1, получаем:

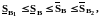
что и требовалось доказать.

Следствие. Множество всех нижних сумм Дарбу ограничено сверху (например, любой верхней суммой Дарбу), а следовательно имеет точную верхнюю грань:

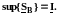
Это число называется нижним интегралом Дарбу. Аналогично, существует и верхний интеграл Дарбу:

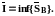
Ясно, что для любого разбиения B справедливо:

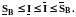
Перейдём теперь к основному результату раздела.

Теорема 1. Если f(x) непрерывна на [a, b], то существует интеграл

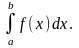
Доказательство. Обозначим: 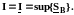Докажем, что число I и является интегралом:

Если B – разбиение отрезка [a, b], то при любом выборе точек _i 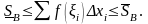Кроме того, мы установили, что 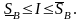Из этих неравенств, очевидно, следует:

Воспользуемся теоремой Кантора о равномерной непрерывности (см. 11.5): так как f(x) непрерывна на [a, b], то она равномерно непрерывна на [a, b], т.е.

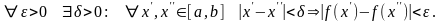
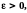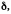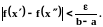Возьмём произвольное найдём такое чтобы при было справедливо Пусть B – разбиение, мелкость которого меньше 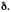Так как наибольшее и наименьшее значения M_i , m_i функции f(x) на отрезке [x_i-1, x_i] достигаются в некоторых точках, то при таком разбиении

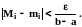
Поэтому

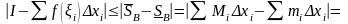
Итак, для любого 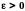мы нашли такое, что если разбиение мельче то любая интегральная сумма отличается от числа I меньше, чем на 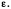По определению, это означает, что Теорема доказана.

Можно доказать интегрируемость и более широкого класса функций. Функция f(x) называется кусочно – непрерывной, если она имеет на [a, b] лишь конечное число разрывов, причём это разрывы 1 рода.

Теорема 2. Кусочно–непрерывные на [a, b] функции интегрируемы.

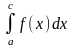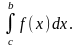Д оказательство. Пусть f(x) имеет в точке x  c разрыв 1 рода, а в остальных точках отрезка [a, b] непрерывна. Рассмотрим отрезок [a, c]. На нём функция либо непрерывна, либо отличается от непрерывной значением в одной точке (в точке c, как на рисунке). По свойству 5, существует . Аналогично, существует и интеграл По свойству аддитивности, тогда существует и что и требовалось. Если точек разрыва несколько, то нужно повторить рассуждение.