14.2 Простейшие методы интегрирования

14.2.1 Таблица интегралов. Каждая формула дифференциального исчисления

F(x)  f(x)

равносильна, как мы теперь знаем, формуле интегрального исчисления:

 F(x) + C.

Для производных основных элементарных функций была составлена таблица производных (см. 12.2.3). Теперь составим таблицу наиболее важных, основных интегралов. Будем пользоваться ей при решении задач, хорошо бы побыстрее запомнить эти формулы. Каждая формула в таблице справедлива на любом интервале, где подинтегральная функция непрерывна.

Таблица основных интегралов.

1. ;

2. ;

3. ,

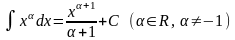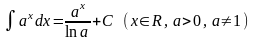в частности ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. .

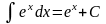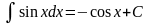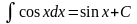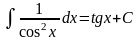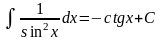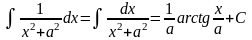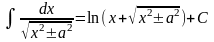Каждую из формул таблицы можно проверить (доказать) с помощью дифференцирования.

Пример 3. Доказать последнюю формулу в таблице.

Решение. Найдём производную функции в правой части формулы:

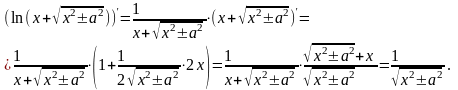
Итак, функция 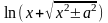является первообразной функции 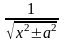, что и требовалось доказать.

Используя таблицу интегралов и свойство линейности (теорема 3), можно вычислять простейшие интегралы.

Пример 4. Вычислить .

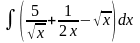Решение. Пользуемся линейностью интеграла:

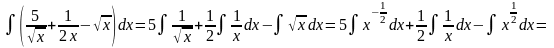
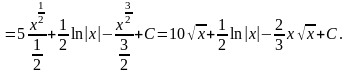
14.2.2 Замена переменной. Рассмотрим самый важный приём для вычисления интегралов: с помощью перехода к другой переменной, упростить интеграл, желательно – свести его к табличному. Имеются два практических подхода к такому преобразованию (теоретически они отличаются мало). Перый из них иногда называют «подведение под знак дифференциала». Этот подход основан на следующей теореме.

Теорема 5. Пусть , u  u(x) – дифференцируемая функция. Тогда .

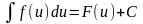Другими словами, любая формула интегрирования остаётся справедливой, если независимую переменную x заменить на произвольную дифференцируемую функцию.

Доказательство. Так как du  u(x)dx, то новая формула запишется так: 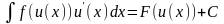. Проверим её, используя правило дифференцирования сложной функции: 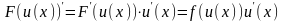. Теорема доказана.

Пример 5. а) 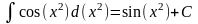. Это соотношение очевидно: к табличной формуле мы применили теорему 5, заменили x на функцию u  x².

б) 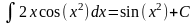. Это соотношение не так очевидно, но ведь 2xdx  d(x²). Поэтому 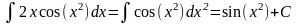. Этот приём и называется подведением под знак дифференциала.

Пример 6. Вычислить .

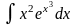Решение. Пользуясь теоремой 2, подведём x² под знак дифференциала: 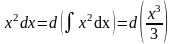. Постоянный множитель можно выносить и за знак дифференциала, и за знак интеграла:

Мы воспользовались табличным интегралом , заменив в нём x на функцию u(x)  x³.

Пример 7. Вычислить .

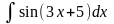Решение. Чтобы воспользоваться табличным интегралом, добьёмся, чтобы под дифференциалом тоже была функция 3x + 5:

.

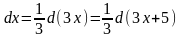Слагаемое 5 мы можем добавить, так как на величину производной (и дифференциала) оно не влияет. Итак,

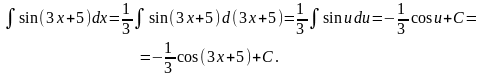
Несколько иной подход к рассматриваемому методу замены переменной (или методу подстановки, это то же самое) основан на теореме 6.

Теорема 6. Пусть 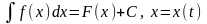– дифференцируемая функция. Тогда .

Ясно, что теорема 6 – лишь немного другая формулировка теоремы 5, её доказательство также следует из правила дифференцирования сложной функции:

.

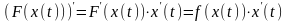Пример 8. Вычислить .

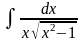Решение. Сделаем подстановку 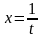(т. е. перейдём от переменной x к переменной t ). Вспомогательные вычисления размещаем в прямых скобках:

.

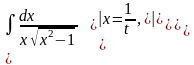Замечание. Умение подобрать нужную подстановку достигается тренировкой. Рекомендации есть лишь в некоторых частных случаях, общих правил нет.

Пример 9. Вычислить 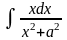. Здесь a – некоторое число.

Решение. Сделаем замену переменной по формуле: x² + a²  u. Вычисляя дифференциал от обеих частей, получим:

d(x²+a²)  2xdx  du.

Теперь перейдём к интегралу по переменной u:

.

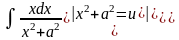Конечно, то же самое получается с помощью подведения под знак дифференциала:

.
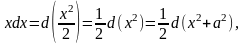
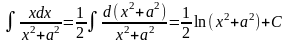