12 Производная и дифференциал

12.1 Определение производной

Одним из основных в математическом анализе является понятие производной. Прежде чем дать точное его определение, рассмотрим задачу о скорости, при решении которой и возникло это понятие.

Пусть материальная точка движется по прямой, а функция s  s(t) определяет зависимость пройденного точкой пути s от времени t. Чтобы найти скорость точки в момент t  t₀ , рассмотрим промежуток времени от t₀ до t₀ + t. За это время точка пройдёт путь s  s(t₀ + t) – s(t₀). Средняя скорость на этом участке равна

.

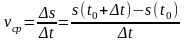Средняя скорость зависит от t, но чем меньше t, тем точнее v_cр будет выражать истинную скорость точки в момент времени t₀. Значит, скорость точки в момент времени t₀ равна пределу:

.

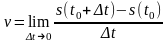Поэтому, если мы хотим уметь вычислять скорость при разных законах движения, нам нужно научиться вычислять такой предел для разных функций.

Заметим, что мы пользовались интуитивным пониманием скорости. Если рассуждать более строго, то последняя формула есть определение: скоростью называется предел указанного вида. Такое определение, как мы видим, хорошо согласуется с интуитивными представлениями.

Перейдём к понятию производной. Пусть функция f(x) определена в окрестности точки x₀ (включая саму точку x₀; здесь рассматривается не проколотая, а обычная окрестность). Дадим приращение x аргументу, т. е. рассмотрим число x₀ + x, также лежащее в этой окрестности. Величина

f  f(x₀ + x) – f(x₀)

называется приращением функции. Если существует конечный предел:

,

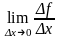то он называется производной функции f(x) в точке x₀, и обозначается f (x₀). В этом случае функция f(x) называется дифференцируемой в точке x₀.

Итак, производная f (x₀) функции f(x) в точке x₀ это число. Однако, меняя точку, можно рассмотреть функцию:

x  f (x),

сопоставляющую каждому x (из некоторого множества) значение производной функции f в точке x. Эта функция обозначается f (x) и также называется производной функции f(x). Отображение f(x)  f (x) называется дифференцированием. Для производной используются и другие обозначения :

.

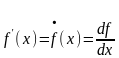Последняя запись читается так: «дэ эф по дэ икс», нужно рассматривать её как единый символ, обозначающий функцию, а не как дробь.

Если к функции f (x) снова применить операцию дифференцирования, то получится производная второго порядка или, короче, вторая производная:

.

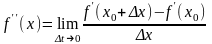Аналогично определяются и производные более высоких порядков:

f (x)  (f (x)), … , f ⁽ⁿ⁾(x)  (f ^(n–1)(x)).

Используются также обозначения:

.

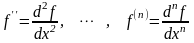Возвращаясь к задаче о скорости, можно теперь сказать, что скорость точки в данный момент времени t₀ есть производная функции s(t) при t  t₀. Скорость может зависеть от времени: v  v(t). Тогда производная функции v(t) есть «скорость изменения скорости», т. е. ускорение: a(t)  v (t)  s (t).

Перейдём к примерам вычисления производных.

Пример 1. Производная постоянной функции равна 0. Действительно, пусть f(x)C (x). Вычислим производную в произвольной точке x:

.

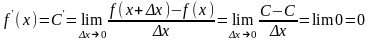Пример 2. Вычислим производную синуса:

.

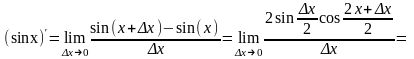
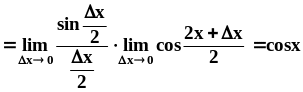Поясним все действия подробно. Первое равенство – определение производной. Второе – результат применения тригонометрической формулы: 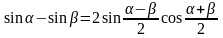. Затем предел произведения функций мы заменили произведением их пределов. Первый сомножитель – это первый замечательный предел, он равен 1. Второй сомножитель вычисляется простой подстановкой 0 вместо x, так как cosx – непрерывная функция. Итак, в любой точке x

( sinx )  cosx.

Заметим, что при вычислении предела x  0, а x мы рассматриваем как постоянное число – это точка, в которой вычисляется производная.

Пример 3. Производная косинуса: (cosx)  – sinx. Здесь вычисления аналогичны:

.

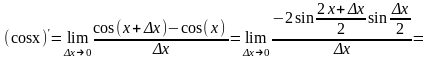
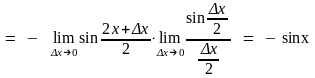Пример 4. Производная показательной функции:

(a^x)  a^x lna.

Действительно,

.

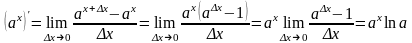В последнем действии мы использовали следствие 1 из 11.4.2. При a  e получаем, в частности, формулу:

(e^x)  e^x.

Пример 5. Производная степенной функции:

(x^)   x^{ –1} .

Действительно,

.Здесь использовано следствие 2 из 11.4.2.

Пример 6. Производная логарифмической функции:

.

Действительно,

.

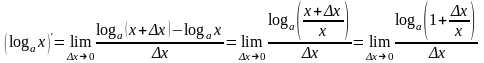Перейдём к более удобным натуральным логарифмам по формуле: 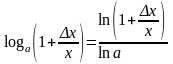, а также воспользуемся одной из основных эквивалентностей бесконечно малых: 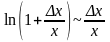( при x  0 ). Продолжаем вычисление:

.

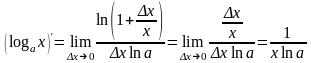Требуемая формула доказана. Особенно простой вид она имеет для натурального логарифма: .

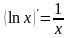Пример 7. Найти вторую производную функции y  sinx в точке .

Решение. По формулам, полученным в примерах 2, 3 имеем:

y­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­  (sinx)  cosx,

y  (sinx)  (cosx)  – sinx.

В частности, 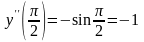. Заметим: мы сначала нашли производную в произвольной точке x, и лишь затем подставили вместо x требуемое число. Запись 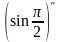была бы неправильной, в ней нарушен порядок действий. Можно использовать такую запись: .

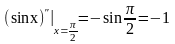Установим связь между дифференцируемостью и непрерывностью функции.

Теорема 1. Если f(x) дифференцируема в x₀, то f(x) непрерывна в x_0.

Доказательство. Дифференцируемость означает, что существует конечная производная в точке x₀:

.

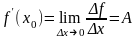Тогда функция 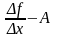является бесконечно малой при x  0. Обозначим её (x). Тогда f  Ax + (x) x и предел приращения f, очевидно, равен 0:

.

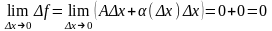По определению, это значит, что f(x) непрерывна при x  x₀.

Обратная теорема не справедлива: функция может быть непрерывной, но не иметь производной.

Пример 8. Функция f(x)  x непрерывна, но не дифференцируема при x  0 , Действительно: f(0)  0, 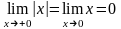, 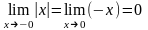. Непрерывность функции установлена. При вычислении производной предел слева оказывается отличным от предела справа:

,

.

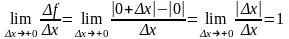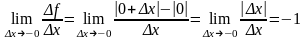Следовательно, не существует.

Если в определении производной рассматривать односторонний предел, то получим понятие односторонней производной. Ясно, что дифференцируемость функции означает совпадение её левой и правой производных.

В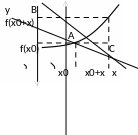 заключение раздела рассмотрим геометрический смысл понятия «производная». Для этого рассмотрим график функции y  f(x). Возьмём точку x₀ и дадим приращение аргументу x. Соответствующие точки A, B на графике имеют ординаты f(x₀), f(x₀ + x). Проведём через них прямую линию, она называется секущей. Угол наклона секущей, т. е. угол между секущей и осью Ox, обозначим . Из прямоугольного треугольника АВС найдем tg:

.

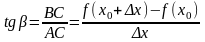Теперь будем уменьшать x. При этом точка B будет приближаться к точке A, угол наклона секущей будет изменяться. Предельное положение, которое стремится занять секущая при x  0, называется касательной к графику функции y  f(x) в точке A. Угол наклона касательной, очевидно, равен пределу переменного угла :

.

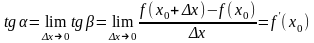Итак, производная равна тангенсу угла наклона (т. е. угловому коэффициенту) касательной.

Теперь мы можем в общем виде записать уравнение касательной к графику функции y  f(x), проведённой в точке (x₀, y₀). Прямая, проходящая через точку (x₀, y₀) и имеющая угловой коэффициент k, задаётся уравнением:

y – y₀  k( x – x₀ ).

Значит уравнение касательной имеет вид:

y – y₀  f (x₀)( x – x₀ ).

Здесь y₀  f(x₀). Прямая, проходящая через ту же точку (x₀, y₀) перпендикулярно касательной, называется нормалью к кривой. Так как условие перпендикулярности прямых с угловыми коэффициентами k₁, k₂ имеет вид: k₁k₂  –1 (см. раздел 5.5, часть 1), то получаем (если f (x₀)  0 ) уравнение нормали:

.

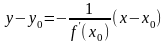Если же f (x₀)  0 , т.е. касательная горизонтальна и имеет уравнение y  y₀, то нормаль будет параллельной оси OY ; её уравнение в этом случае: x  x₀.

Пример 9. Найти уравнения касательной и нормали к графику функции y  x³ в точке (2, 8).

Решение. Вычислим производную в данной точке. Производная степенной функции вычислялась в примере 5, здесь у нас – частный случай:

.

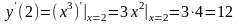Угловой коэффициент касательной равен 12, поэтому её уравнение имеет вид:

y – 8  12 (x – 2), или y  12x – 16.

Уравнение нормали :

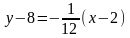, или x + 12y – 98  0.