
- •35. Линии магнитной индукции
- •36. Закон Био-Савара-Лапласа
- •40. Движение заряженных частиц в магнитном поле
- •41. Циркуляция вектора в магнитного поля в вакууме
- •42. Магнитные поля соленоида и тороида
- •43. Поток вектора индукции магнитного поля. Теорема Гаусса для индукции магнитного поля.
- •44. Работа по перемещению проводника и контура с током в магнитном поле
- •45. Опыты Фарадея и следствия их них
- •46. Основной закон электромагнитной индукции ( закон Фарадея)
- •47. Правило Ленца. Эдс индукции в неподвижных проводниках
- •48. Индуктивность контура. Явление самоиндукции
- •49. Вращение рамки в магнитном поле. Вихревые токи
- •50.Токи размыкания/замыкание цепи
- •51Взаимная индукция
- •52.Трансформаторы и энергия магнитного поля
- •54. Намагниченность и магнитное поля веществе
- •55. Закон полного тока для магнитного поля вещества ( теорема о циркуляции вектора b)
- •56. Условия на границе раздела магнетиков
- •57. Ферромагнетики и их свойства.
- •58. Вихревое, электростатическое поле.
- •59. Ток смещения
- •60. Уравнение Максвелла для электромагнитного поля
- •61. Свободные колебания в идеализированном колебательном контуре
- •59. Ток смещения
- •60. Уравнение Максвелла для электромагнитного поля
- •61. Свободные колебания в идеализированном колебательном контуре
- •62.Вынужденные электромагнитные колебания
- •63.Переменный ток. Ток, текущий через резистор.
- •64.Переменный ток текущий через катушку индуктивности (l)
- •65. Переменный ток, текущий через конденсатор
- •66. Цепь переменного тока, содержащая резистор, конденсатор, катушку
- •67. Резонанс напряжений (последовательный резонанс)
- •68. Резонанс токов и параллельный резонанс
- •Резонанс тока
- •69. Мощность, выделяемая в цепи переменного тока
- •70. Преобразование и передача электроэнергии
- •71. Дифференциальные уравнения электромагнитных волн
- •72. Энергия и импульс электромагнитной волны.
- •73. Зонная теория твердых тел
- •74 . Металлы, диэлектрики и полупроводники по зонной теории
- •75.Собственная проводимость полупроводников
- •76. Примесная проводимость полупроводников
58. Вихревое, электростатическое поле.
Максвелл высказал гипотезу что всякая перемещение магнитного поля возбуждающую в окружающем пространстве электрическое поле ,которое является причиной возникновения индукционного тока в конденсаторе. Конденсатор играет второстепенную роль, является лишь прибором.→
Согласно
Максвеллу, изменяется во времени
магнитное поле порождая электрическое
поле циркуляции которого может быть
представлена в таком виде:
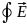 d
d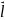 =-
=-
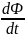 ; Ф=
; Ф=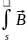 d
d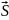
d
=-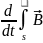 d
d
d
=-∫
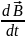 d
1-е уравнение Максвелла
d
1-е уравнение Максвелла
Где символ частной производной подчеркивает лишь тот факт, что d
является функцией не только времени.
Операция дифференцирования и интегрирования меняют местами, т.к. поверхность и контур неподвижны, т.е. не изменяется во времени.
59. Ток смещения
Согласно Максвеллу всякое переменное магнитное поле возбуждает в пространстве вихревое электрическое поле, а изменение электрического поля вызывает в пространстве появление вихревого магнитного поля, взаимосвязь электрических и магнитных полей.
Для установления количественных характеристик между изменением электрического и вызываемым им магнитным полем Максвелл ввел понятие ток смещения.
В электрической цепи содержится конденсатор, то есть разрыв, переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле как если бы между обкладками конденсатора существовал какой-то ток смещения, равный по величине току в проводящих проводах. Величина тока смещения равна по величине току проводимости I.
Для конденсатора: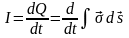

σ – поверхностная плотность
заряда на обкладках конденсатора.

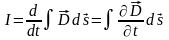
Поверхностная плотность заряда на обкладках равна D.
Подынтегральное выражение можно рассматривать как частный случай скалярного произведения, когда два вектора взаимно параллельны.
Так как силу тока можно представить как поток вектора плотности тока, то есть ток I может быть представлен как интеграл.
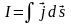 сравнивая можно записать
сравнивая можно записать
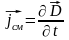
jсм - плотность тока смещения.
В диэлектрике:
Так как электрическое смещение в
диэлектрике D определяется
следующим образом:
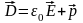 , то ток смещения будет определятся
следующим образом:
, то ток смещения будет определятся
следующим образом:
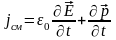 ,
где слагаемое
,
где слагаемое
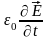 есть плотность тока смещения в вакууме,
а
есть плотность тока смещения в вакууме,
а
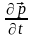 есть плотность тока поляризации, то
есть тока обусловленного упорядоченным
движением электрического заряда в
диэлектрике( то есть смещения зарядов
в неполярных молекулах и поворот диполей
в полярных молекулах)
есть плотность тока поляризации, то
есть тока обусловленного упорядоченным
движением электрического заряда в
диэлектрике( то есть смещения зарядов
в неполярных молекулах и поворот диполей
в полярных молекулах)
Возбуждение магнитного поля этими токами поляризации правомерно, так как эти токи поляризации не отличаются от токов проводимости.
Слагаемое
обусловлено только изменением
электрического поля во времени, но тоже
вызывает магнитное поле. Это принципиально
новое утверждение Максвелла, то есть
даже в вакууме всякое изменение
электрического поля приводит к
возникновению в окружающем пространстве
магнитного поля. По Максвеллу полный
ток замкнут, то есть в контуре содержащем
конденсатор существует ток проводимости
который обрывается лишь перед
конденсатором, а в конденсаторе между
концами возникает ток смещения, поэтому
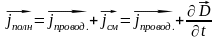
Из всех свойств присущих току проводимости Максвелл приписал току смещения лишь одно свойство – способность создавать в окружающем пространстве магнитное поле.
Обобщая теорию о перемещении
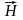 ,
можно записать что циркуляция вектора
равна току
,
можно записать что циркуляция вектора
равна току
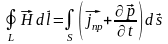 - 2-ое уравнение Максвелла.
- 2-ое уравнение Максвелла.
