
- •35. Линии магнитной индукции
- •36. Закон Био-Савара-Лапласа
- •40. Движение заряженных частиц в магнитном поле
- •41. Циркуляция вектора в магнитного поля в вакууме
- •42. Магнитные поля соленоида и тороида
- •43. Поток вектора индукции магнитного поля. Теорема Гаусса для индукции магнитного поля.
- •44. Работа по перемещению проводника и контура с током в магнитном поле
- •45. Опыты Фарадея и следствия их них
- •46. Основной закон электромагнитной индукции ( закон Фарадея)
- •47. Правило Ленца. Эдс индукции в неподвижных проводниках
- •48. Индуктивность контура. Явление самоиндукции
- •49. Вращение рамки в магнитном поле. Вихревые токи
- •50.Токи размыкания/замыкание цепи
- •51Взаимная индукция
- •52.Трансформаторы и энергия магнитного поля
- •54. Намагниченность и магнитное поля веществе
- •55. Закон полного тока для магнитного поля вещества ( теорема о циркуляции вектора b)
- •56. Условия на границе раздела магнетиков
- •57. Ферромагнетики и их свойства.
- •58. Вихревое, электростатическое поле.
- •59. Ток смещения
- •60. Уравнение Максвелла для электромагнитного поля
- •61. Свободные колебания в идеализированном колебательном контуре
- •59. Ток смещения
- •60. Уравнение Максвелла для электромагнитного поля
- •61. Свободные колебания в идеализированном колебательном контуре
- •62.Вынужденные электромагнитные колебания
- •63.Переменный ток. Ток, текущий через резистор.
- •64.Переменный ток текущий через катушку индуктивности (l)
- •65. Переменный ток, текущий через конденсатор
- •66. Цепь переменного тока, содержащая резистор, конденсатор, катушку
- •67. Резонанс напряжений (последовательный резонанс)
- •68. Резонанс токов и параллельный резонанс
- •Резонанс тока
- •69. Мощность, выделяемая в цепи переменного тока
- •70. Преобразование и передача электроэнергии
- •71. Дифференциальные уравнения электромагнитных волн
- •72. Энергия и импульс электромагнитной волны.
- •73. Зонная теория твердых тел
- •74 . Металлы, диэлектрики и полупроводники по зонной теории
- •75.Собственная проводимость полупроводников
- •76. Примесная проводимость полупроводников
46. Основной закон электромагнитной индукции ( закон Фарадея)
Обобщая результаты опытов Фарадей показывал, что вок.раз., когда происходят изменения магнита Ф сквозь площадку, ограниченную контуром, в контуре возникает индукционный ток. Его наличие в контуре указывает на то что в цепи возникает ЭДС, которое носит название ЭДС электромагнитной индукции.
При всяких изменениях м. Ф пронизывающий контур проверка послед. возникает ЭДС индукции :
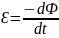 т.к. Ф=ВS*cosϕ
ЭДС возник. Не зависит от способа
изменения магнитного потока.
т.к. Ф=ВS*cosϕ
ЭДС возник. Не зависит от способа
изменения магнитного потока.
Вывод закона Фарадея из закона сохранения энергии: пусть промежуток с током ӏ, помещается в одно магнитное поле, которое I плоскости контура, момент свободного перемещения. Тогда согласно закону сохранения энергии, А источник тока за время dt расходится на образование в проводнике достаточного тепла и на перемещение промежутка с током.
ԐIdt=I2
Rdt+IdФ Ԑdt= I Rdt+IdФ
Ԑ=dФ/dt=IR
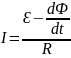
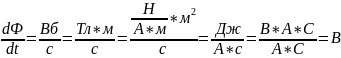
47. Правило Ленца. Эдс индукции в неподвижных проводниках
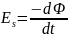 (1) закон электромагнитной индукции
Фарадея.
(1) закон электромагнитной индукции
Фарадея.
Знак «—» показывает, что увеличение
потока (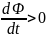 )
вызывает ЭДС
)
вызывает ЭДС
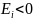 , т. е. поле индукционного тока направлено
навстречу потоку; уменьшение потока
, т. е. поле индукционного тока направлено
навстречу потоку; уменьшение потока
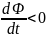 вызывает
вызывает
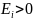 ,
т. е. направления потока
и поля индукционного тока совпадают.
Знак «—» в формуле (1) соответствует
правилу Ленца (1833) — общему правилу
для нахождения направления индукционного
тока.
,
т. е. направления потока
и поля индукционного тока совпадают.
Знак «—» в формуле (1) соответствует
правилу Ленца (1833) — общему правилу
для нахождения направления индукционного
тока.
Правило Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающему этот индукционный ток.
Согласно
закону Фарадея, возникновение ЭДС
электромагнитной индукции возможно и
в случае неподвижного контура, находящегося
в переменном магнитном поле. Однако
сила Лоренца на неподвижные заряды не
действует, поэтому в данном случае ею
нельзя объяснить возникновение ЭДС
индукции. Максвелл для объяснения ЭДС
индукции в неподвижных проводниках
предположил, что всякое переменное
магнитное поле возбуждает в окружающем
пространстве электрическое поле, которое
и является причиной возникновения
индукционного тока в проводнике.
Циркуляция вектора EВ
этого ноля по любому неподвижному
контуру L проводника
представляет собой ЭДС электромагнитной
индукции:
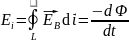 .
.
48. Индуктивность контура. Явление самоиндукции
Электрический
ток, текущий в замкнутом контуре, создает
вокруг себя магнитное поле, индукция
которого, по закону Био —Савара —
Лапласа, пропорциональна току. Сцепленный
с контуром магнитный поток Ф поэтому
пропорционален току в контуре:
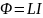 (1)
где L — коэффициент
пропорциональности, называемый
индуктивностью контура.
(1)
где L — коэффициент
пропорциональности, называемый
индуктивностью контура.
При изменении силы тока в контуре будет изменяться также и сцепленный с ним магнитный поток; следовательно, в контуре будет индуцироваться ЭДС. Возникновение ЭДС индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией.
Из выражения (1) определяется единица индуктивности генри (Гн): 1 Гн — индуктивность такого контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб: 1 Гн = 1 Вб/А = 1 В • с/А.
Рассчитаем индуктивность бесконечно длинного соленоида. Полный магнитный поток
сквозь
соленоид (потокосцепление) равен
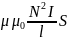 .
Подставив это выражение в формулу (1),
получим
.
Подставив это выражение в формулу (1),
получим
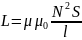 ,
(2)
т.е. индуктивность соленоида зависит
от числа N витков соленоида,
его длины
,
(2)
т.е. индуктивность соленоида зависит
от числа N витков соленоида,
его длины
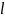 ,
площади S и магнитной
проницаемости µ вещества, из которого
изготовлен сердечник соленоида.
,
площади S и магнитной
проницаемости µ вещества, из которого
изготовлен сердечник соленоида.
Можно показать, что индуктивность контура в общем случае зависит только от геометрической формы контура, его размеров и магнитной проницаемости той среды, в которой он находится. В этом смысле индуктивность контура — аналог электрической емкости уединенного проводника, которая также зависит только от формы проводника, его размеров в диэлектрической проницаемости среды.
Применяя к явлению самоиндукции закон
Фарадея, получим, что ЭДС самоиндукции
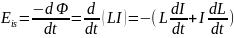 .
.
Если контур
не деформируется и магнитная проницаемость
среды не изменяется (в дальнейшем будет
показано, что последнее условие
выполняется не всегда), то L
— const и
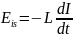 (3)
где знак «—» обусловлен правилом
Ленца, согласно которому наличие
индуктивности в контуре приводит к
замедлению изменения тока в нем.
(3)
где знак «—» обусловлен правилом
Ленца, согласно которому наличие
индуктивности в контуре приводит к
замедлению изменения тока в нем.
Если ток со
временем возрастает, то
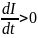 и
и
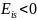 , т.е. ток самоиндукции направлен навстречу
току, обусловленному внешним источником,
и замедляет его возрастание. Если ток
со временем убывает, то — < 0 и
, т.е. ток самоиндукции направлен навстречу
току, обусловленному внешним источником,
и замедляет его возрастание. Если ток
со временем убывает, то — < 0 и
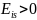 , т. е. индукционный ток имеет такое же
направление, как и убывающий ток в
контуре, и замедляет его убывание. Таким
образом, контур, обладая определенной
индуктивностью, приобретает электрическую
инертность, заключающуюся в том, что
любое изменение тока тормозится тем
сильнее, чем больше индуктивность
контура.
, т. е. индукционный ток имеет такое же
направление, как и убывающий ток в
контуре, и замедляет его убывание. Таким
образом, контур, обладая определенной
индуктивностью, приобретает электрическую
инертность, заключающуюся в том, что
любое изменение тока тормозится тем
сильнее, чем больше индуктивность
контура.
