42. Магнитные поля соленоида и тороида
Рассчитаем, применяя теорему о циркуляции, индукцию магнитного поля внутри соленоида. Рассмотрим соленоид длиной /, имеющий ЛГвитков, по которому течет ток. Длину соленоида считаем во много раз больше, чем диаметр его витков, т.е. рассматриваемый соленоид бесконечно длинный.
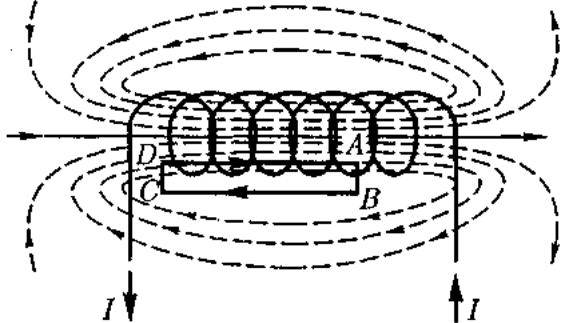
Экспериментальное изучение магнитного поля соленоида (см. рис. 164, б) показывает, что внутри соленоида поле является однородным, вне соленоида — неоднородным и очень слабым. На рис. 177 представлены линии магнитной индукции внутри и вне соленоида. Чем соленоид длиннее, тем меньше магнитная индукция вне его. Поэтому приближенно можно считать, что поле бесконечно длинного соленоида сосредоточено целиком внутри него, а полем вне соленоида можно пренебречь. Для нахождения магнитной индукции В выберем замкнутый прямоугольный контур ABCDA, как показано на рис. 177. Циркуляция вектора В по замкнутому контуру А В CD А, охватывающему все Nвитков, согласно
равна
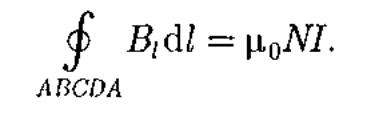
43. Поток вектора индукции магнитного поля. Теорема Гаусса для индукции магнитного поля.
Поток вектора магнитной индукции—скалярная величина, численно равная скалярному произведению В на dS.
cosα
]Направление вектора dS совпадает с единственным вектором к нормали к dS.
Поток вектора В связывают с контуром, по которому течет ток, тогда положительное направление нормали к dS связывается с направлением тока в контуре правилом правого винта.
Магнитный поток сквозь произвольную поверхность:
Если поле
однородно, а контур плоский, то: Ф=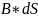
[1Вб]
1Вб—магнитный поток, проходящий через плоскую поверхность площадью 1 м2 , расположенную перпендикулярно однородному магнитному полю величиной в 1Тл.
Теорема Гаусса для индукции магнитного поля: поток вектора магнитной индукции сквозь произвольную замкнутую поверхность
.
Эта теорема отражает отсутствие в природе магнитных зарядов как источников магнитного поля, т. е. линии магнитной индукции не имеют не начала не конца, т.е. являются замкнутыми.
44. Работа по перемещению проводника и контура с током в магнитном поле
Пусть проводник длиной L и с током I находится в однородном магнитном поле и может однородно перемещаться.
работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником.
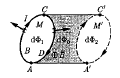
Разобьем замкнутый контур на 2 проводника: ABC и CDA, тогда работа по перемещению всего контура:
Согласно ранее полученной зависимости работа dA определяется:
Знак «-» возникает потому что Fa образует с направлением перемещения тупой угол.
45. Опыты Фарадея и следствия их них
Опыт 1: Если в замкнутый на гальванометр соленоид вдвигать или выдвигать постоянный магнит, то в моменты его вдвигания или выдвигания наблюдается отклонение стрелки гальванометра (возникает индукционный ток); направления отклонений стрелки при вдвигании и выдвигании магнита противоположны. Отклонение стрелки гальванометра тем больше, чем больше скорость движения магнита относительно катушки. При изменении полюсов магнита паправление отклонения стрелки изменится.
Для получения индукционного тока магнит можно оставлять неподвижным, тогда нужно относительно магнита передвигать соленоид.
Опыт 2: если вместо постоянного магнита использовать другой соленоид, по которому протекает ток, то отклонения стрелки наблюдаются в моменты включения и выключения, а так движения катушек друг относительно друга.
Вывод 1: индукционный ток возникает всегда, когда происходит изменение тока.
Вывод 2: сила индукционного тока не зависит от способа изменения потока магнитной индукции, а определяется лишь скоростью его изменения.
Электромагнитная индукция – явление, заключается в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного.