67. Резонанс напряжений (последовательный резонанс)

Резонанс напряжений— явление резкого возрастания амплитуды силы тока в контуре при совпадении циклической частоты колебаний внешнего источника с собственной частотой контура.

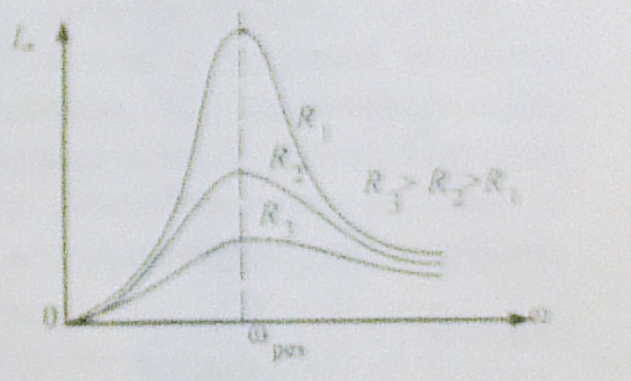
Зависимость I_m от ω графически изображена на рисунки, где показаны три кривые, соответствующие трем различным значениям активного сопротивления R. Чем меньше R , чем больше при прочих равных условиях I_m и тем острее максимум кривых.

Резонанс напряжений:

1. сопротивление контура активное и минимальное

2. ток в контуре находится в фазе с действующим ЭДС и определяется величиной омического сопротивления.

Падение напряжения на индуктивности= по абсолютной величине напряжению на емкости, однако они сдвинуты друг относительно друга на П

ω_рез=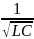 ; U_L=U_{C ;} I_m=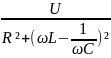 = 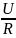; tgρ =

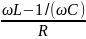
68. Резонанс токов и параллельный резонанс

Рассмотрим цепь переменного тока, содержащую параллельно включенные конденсатор и катушку индуктивностью L.

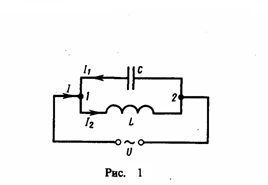Рассмотрим ветвь 1-2. В общем случаи ветвь I_c=I_mcos(ωt-f)

tgρ = → ∞ ; R→0; L→0

f=3/2 П+2Пn ;n=0,1,2…

I_c=I_mcos(ωt-f₂)

f₂=П/2+2Пn

f-f₂=П точки будут иметь противоположные фазы. Ток в подводящих проводах будет определяться разностью токов

I=(I_mc-I_ml)=U_m(ωL-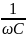 )=0 , т.к ωL= при резонансе

Явление резонансов тока- явление резкого уменьшения амплитуды силы тока в неразветвленной части цепи, питающие параллельно включенные конденсатор и индуктивность при приближении частоты приложенной к резонансной частоте ω_рез=

Амплитуда силы тока в неразветвленной части цепи остается =0, т.к. мы пренебрегли активным сопротивлением.

Если учесть сопротивление R, то разность фаз f-f₂ не будет равна строго П, при резонансе токов амплитуда силы токов будет отличаться от нуля, но примет наименьшее значение.

Резонанс тока

1)Сопротивление тока активное и max.

2)Напряжение на ёмкости индуктивности находится на фазе с действующим ЭДС. Напряжение на ёмкости = напряжению индукции, и ЭДС источника. Ток в индуктивности по абсолютной величине равной току в ёмкости, но сдвинуты относительно друг от друга на π.

69. Мощность, выделяемая в цепи переменного тока

Т.к. в общем случае в цепи переменного тока существует сдвиг фаз, то рассмотрим значение мощности переменного тока: P(t)=I(t)U(t) (1)

U(t)=U_m cos t

I(t)=I_m cos ( t-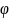 ) подставим эти выражения в (1)

P(t)= I_m U_m cos t cos ( t- )= I_m U_m(cos² t cos + sin t cos t sin )

Интерес представляет средняя мощность: <P(t)>=0.5 I_m U_m cos = сдвиг между током и напряжением

Согласно векторной диаграмме U_m cos = R I_m

Такую же мощность, как в цепи постоянного тока развивает максимальный ток: I= I_m /

Поэтому действующие значения переменного тока и напряжения: I= I_m / U= U_m /

учитывая эти действующие значения получаем среднюю мощность: <P>=IU cos

70. Преобразование и передача электроэнергии

Широкое применение переменного тока в промышленности связано с удобством его преобразования. Почему же из всех форм переменного сигнала наибольшее распространение получили синусоидальные токи? Только при использовании синусоидальных токов удается сохранить формы кривизны направления во всех участках линейной электрической цепи

Для такого тока, при наличии в цепи реактивного напряжения возникает сдвиг по фазе, что приводит к появлению cos в <P>. Потребителю обычно подаются определенные значения напряжения. При малых значениях cos ,( т.е. больших сдвигах фаз между токами напряжения) для полного определения мощности необходим больший ток. Больший ток приводит к большим потерям в проводящих проводах, поэтому для уменьшения потерь необходимо уменьшать сдвиг фаз между токами напряжения.