35. Линии магнитной индукции

Линии магнитной индукции, т.к. магнитное поле – силовое поле, то его по аналогии с электрическим изображением с помощью линий магнитной индукции – это линии, насыщения к которым в каждой точке совпадает с направлением вектора .

И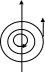 х направление совпадает с направлением 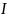, правило правого винта.

Эти линии замкнутые и охватывают проводники с током. Линии всегда замкнуты и охватывают проводника с током, этим они отличаются от линий напряженности электрического поля, которые начинаются с «+» и заканчиваются на «-», т.е. разомкнуты.

Принцип суперпозиции магнитных полей:

Магнитная индукция разомкнутого поля, создаётся несколькими токами или движущими зарядами, равна вектору изменения магнитной индукции полей, издающим каждым током в суперпозиции.

Пример применения суперпозиции:

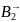A

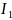
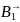
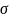
36. Закон Био-Савара-Лапласа

Элемент проводника с током 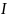, элементом dl создаёт вокруг себя магнитное поле с индукцией

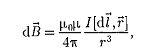где r – радиус-вектор; 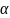-- угол между элементами dl и r.

Н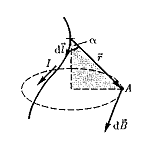 аправление dB определяется по правилу правого винта:

Применение закона Био-Савара-Лапласа для определения B прямого проводника с током.

, ,

,

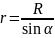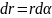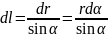
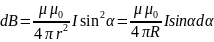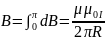
Магнитное поле в центре произвольного тела.

Пусть имитирует круг тока

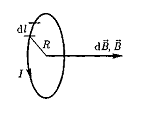r =R, sin =1

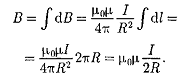
№ 37 Закон Ампера

Магнитное поле оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования действия магнитного поля на различные проводники с током, А.Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dL с током, находящегося в магнитном поле, равна:

dF =I[BdL] где dL-вектор, по модулю равный dL и совпадающий по направлению с током, В-вектор магнитной индукции.

Направление вектора dF может быть найдено, по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца- по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.

Модуль силы Ампера:

dF =IBdL*sinα

где α-угол между векторами dL и dB.

Закон Ампера применяется для определения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I₁ и I_2, расстояние между которыми равно R. Каждый из проводников создает магнитное поле, которое действует по закону Ампера на другой проводник с током.

№ 38. Магнитная постоянная. Единица В,Н

Если два параллельных проводника с током находятся в вакууме (µ=1), то сила взаимодействия на единицу длины проводника:

=

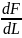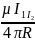
Для нахождения числового значения µ₀ воспользуемся определением ампера, согласно которому =2*10^-7Н/м при I₁=I₂=1A и R-1м. Подставим это значение в формулу приведенную выше и получим: µ₀=4π *10^-7Гн/м.

Единица индуктивности-генри(Гн).

Закон Ампера позволяет определить единицу магнитной индукции В. Предположим, что элемент проводника dL с током перпендикулярен направлению магнитного поля. Тогда закон ампера:

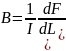
Единица магнитной индукции-тесла(Тл): 1Тл- магнитная индукция такого однородного магнитного поля, которое действует силой 1Н на каждый метр длины прямолинейного проводника, расположенного перпендикулярно направлению поля, если по этому проводнику течет 1А:

1Тл=1Н/(А*м)

Так как µ₀=4π*10^-7Н/А², а в случае вакуума (µ=1),а В=µ₀Н, для данного случая

Н=

Единица напряженности магнитного поля- ампер на метр(А/м): 1 А/м-напряженность такого поля, магнитная индукция которого в вакууме равна 4π*10^-7Тл.

№39. Действие магнитного поля на движущиеся заряд

Опыт показывает, что магнитное поле действует не только на проводники с током, но и на отдельные заряды, движущиеся на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и выражается формулой:

F=Q[uB], где В-индукция магнитного поля, в котором заряд движется.

Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора u, то отогнутый большой палец покажет направление силы, действующей на положительный заряд. На отрицательный заряд сила действует в положительном направлении. Модуль силы Лоренца:

F=QuBsinα где: α-угол между u и B.

Магнитное поле не действует на покоящийся электрический заряд. В этом существенное отличие магнитного поля от электростатического. Магнитное поле действует только на движущиеся в нем заряды.

Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, поэтому она изменяет только направление этой скорости, не меняет только направление этой скорости, не меняя ее модуля. Следовательно, сила Лоренца работы не совпадают. Иными словами, постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется.

Если движущая частица находится одновременно во внешнем магнитном и электрическом полях, то сила Лоренца определяется суммай векторов:

F_Л=QE+Q[BU]