4.2 Построение области устойчивости
Область устойчивости – это геометрическое место точек на плоскости параметров системы, соответствующих ее устойчивому состоянию. Номограмма с указанной на ней областью устойчивости заменяет вычисления по формулам выполнением простейших геометрических построений с помощью линейки и считывания отсчетов. Применяется для исследования зависимости устойчивости от параметров системы, ее чувствительности к изменению параметров по условиям устойчивости, для обоснованного выбора регулируемых параметров в процессе наладки системы.
Методику построения области устойчивости при использовании критерия Рауса-Гурвица проиллюстрируем на примере системы автоматического управления, структурная схема которой показана на рисунке 4.2.
Пример 2.Используя критерий Рауса-Гурвица построить область устойчивости в плоскости параметров (K, T2) при следующих данных: Т1 = 0,25 с; Т3 = 0,1 с; ΔТ2 = 0,05Т2; коэффициент запаса устойчивости α = 3.
Рисунок 4.2
Решение. Записываем характеристическое уравнение по правилу: сумма многочленов числителя и знаменателя передаточной функции прямого канала равна нулю:
.
Имеем уравнение третьей степени. согласно (4.3) записываем условие устойчивости:
откуда:
Граница между областью устойчивости и неустойчивости в плоскости параметров K и T2 определяется уравнениями:
,
которые
при
с и
с принимают
вид:
с
и
.
границы области устойчивости показаны на рисунке 4.3.
Рисунок 4.3
Система будет
устойчивой при любых настройках
и любых значениях K, лежащих ниже
значений
.
При любых других значениях T2
и K система неустойчива.
Система склонна
к неустойчивости при значениях
коэффициента K близких к граничным
и при неблагоприятных изменениях
постоянных времени T1 и
T3 может потерять устойчивость.
На номограммах выделяют
область допустимых значений параметров,
при которых в реальной системе
гарантируется соблюдение условий
устойчивости. В данной задаче граница
этой области при
и
определяется равенством:
.
Упражнения:
Построить область устойчивости системы (рисунок 4.2) в плоскости параметров (K, T2) при
с;
с;
и
.Дано характеристическое уравнение системы, содержащей внутренний контур обратной связи с коэффициентом связи Kо.с :
где К – регулируемый коэффициент прямого канала системы.
используя критерий Рауса-Гурвица, построить область устойчивости в плоскости параметров (Ко.с , К) при настройке коэффициента в пределах: 0 < Kо.с < 1.
Ответ: Для правильно построенной области Kкр = 40,4 при Kо.с = 0,5.
Система имеет характеристическое уравнение
.
Определите диапазон значений К,
при которых система является устойчивой.
Ответ:
К >
0,63.Дано характеристическое уравнение
.
Определить диапазон значений К,
при которых система является устойчивой.
Ответ:
К <
1/3.На рисунке 4.4 представлена структурная схема системы управления скоростью ленты на розливе жидкости в бутылки, в которой используется червячный подающий механизм. Точное значение скорости ленты поддерживается за счет тахометрической обратной связи.
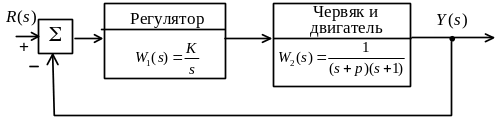
Рисунок 4.4
Определите и представьте графически область устойчивости системы в плоскости параметров К и p.