3. Преобразование структурной схемы

Структурная схема в первоначальном исполнении (например, схема на рисунке 1.2) представляет собой достаточно сложную для расчетов комбинацию звеньев направленного действия, сумматоров и связей между ними. Путем преобразований ее сводят к структурной схеме основной формы, показанной на рисунке 3.1 при .

рисунок 3.1

3.1 Основные правила преобразования

Правила сформулированы для различных схем соединения двух звеньев, передаточные функции которых –  первого звена и – второго звена известны.

Правило 1. Передаточная функция последовательно соединенных звеньев (рисунок 3.2) равна произведению передаточных функций и отдельных звеньев:

. (3.1)

Рисунок 3.2

Например: и .

Тогда 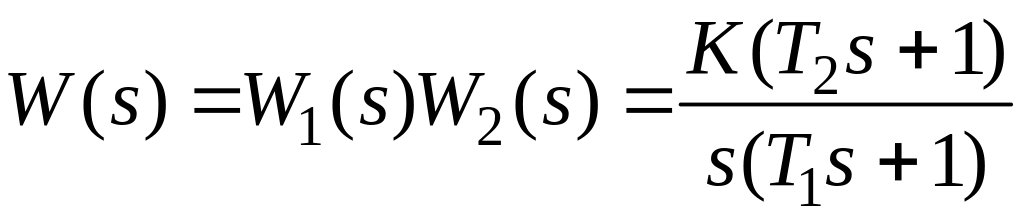, где .

Правило 2. Передаточная функция параллельно соединенных звеньев (рисунок 3.3) равна сумме передаточных функций и отдельных звеньев:

. (3.2)

Примечание: При решении практических задач сумму передаточных функций приводят к общему знаменателю с последующими алгебраическими преобразованиями.

Например: ; .

Тогда

,

где .

Правило 3. Передаточная функция встречно-параллельного соединения звеньев в виде замкнутого контура с отрицательной обратной связью (рисунок 3.4) равна отношению передаточной функции звена в прямой цепи контура к выражению, равному единица плюс произведение передаточных функций и прямой цепи и цепи обратной связи:

. (3.3)

Рисунок 3.3 Рисунок 3.4

Примечания:

а) если правая часть равенства (3.3) после алгебраических преобразований будет содержать множитель

, (3.4)

то при можно в (3.4) пренебречь постоянной времени и записать:

; (3.5)

б) при множитель (3.4) представляют в виде произведения двух сомножителей:

, (3.6)

где и вычисляют по формулам:

; (3.7)

. (3.8)

Например: ; ; Т₁ = 0,12 с; Т₂ = 0,04 с; K₂ = 0,16.

Тогда .

обозначим: Находим с. Так как , то постоянной времени пренебрегаем. Получаем: .

Правило 4. При приведении ко входу контура возмущения , действующего внутри контура (рисунок 3.5), определяют эквивалентное возмущение на входе (рисунок 3.6), равное произведению на обратную передаточную функцию между изображениями переменных и при :

. (3.9)

Такой перенос внешнего возмущения позволяет структурную схему контура преобразовать к схеме простейшего вида.

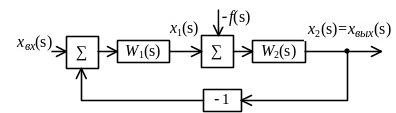
Рисунок 3.5

Рисунок 3.6

Например, в структурной схеме двигателя постоянного тока (рисунок 3.7) статическому моменту сопротивления нагрузки М_СН(s) можно поставить в соответствие эквивалентное возмущение на входе схемы , отображающее напряжение троганья двигателя под нагрузкой,

. (3.10)

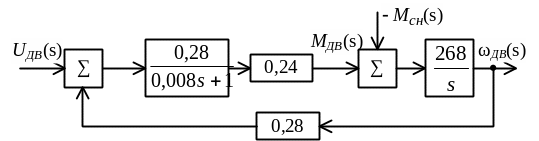
Рисунок 3.7

Тогда передаточная функция прямой цепи:

,

а передаточная функция двигателя как замкнутого контура

.

Так как , то в соответствии с (3.5) получим

.

Отметим, что в (3.10) постоянная времени 0,008 с < 0,04 с. Следовательно, пренебрегая постоянной времени 0,04 с в W_дв(s), можно пренебречь и постоянной времени 0,008 с в (3.10). Структурная схема (рисунок 3.7) принимает вид, показанный на рисунке 3.8.

Рисунок 3.8

Упражнения:

1. Даны два параллельно соединенных звена с передаточными функциями: для первого звена , для второго звена . Определить передаточную функцию соединённых звеньев по следующим передаточным функциям:

а) ;

б) ;

в) .

Ответы:

а) ,

б) ,

в) .

2. По структурной схеме фильтра, изображенной на рисунке 3.9, записать передаточную функцию фильтра при следующих данных:

а) б) в) .

Рисунок 3.9

Ответы:

а) б) в)

3. На рисунке 3.10 показана структурная схема отдельной функциональной части системы управления. Найти её передаточную функцию.

Рисунок 3.10

Ответ: .