2. Передаточные функции звеньев. Временные и частотные характеристики.
К типовым функциям времени (реакциям системы) относятся переходная и импульсная переходная(весовая) функции.
Импульсная или весовая функция представляет собой реакцию звена на единичную импульсную функцию. Весовой функцией звена w(t) называется оригинал (т.е. обратное преобразование Лапласа) передаточной функции, а именно:
(2.1)
Переходная функция представляет собой реакцию звена на единичную ступенчатую функцию и определяется как обратное преобразование Лапласа по формуле:
.
(2.2)
Пример 1:
Определить передаточную функцию объекта
регулирования, если его весовая функция
равна
По таблице оригиналов находим изображения весовой функции, которое и будет является искомой передаточной функцией.
Приведя все дроби к общему знаменателю, получим передаточную функцию в стандартном виде
Пример 2:
Найти весовую функцию системы, если
переходная функция равна
Найдем изображение переходной функции
Убираем нулевой
корень
в знаменателе, принадлежащий входному
воздействию – скачку, получаем
передаточную функцию или изображение
весовой функции
Откуда весовая функция системы
определяется по формуле
Упражнения:
Определите изображения Лапласа для типовых внешних воздействий на систему, графики которых показаны на рисунке 2.1.
а)
– единичное ступенчатое воздействие;
б) – воздействие в виде
–функции;
в) –воздействие, изменяющееся с постоянной
скоростью
;
г) – воздействие, изменяющееся с
постоянным ускорением
;
д) – периодическое воздействие с периодом
колебаний
и амплитудой А.
Рисунок 2.1
Определить изображения Лапласа для следующих воздействий:
а)
б)
в)
г)
д)
е)
Записать изображение весовой функции с
Весовая функция системы равна
Записать изображение переходной
функции.Найти передаточную функцию по известной функции веса
.
а)
б)
в)
По передаточной функции системы найти ее реакцию единичное ступенчатое воздействие (переходную функцию).
а)
б)
Записать изображение реакции на воздействие
,
определить коэффициент передачи в
установившемся режиме для объекта
вида
.
Система имеет коэффициент усиления
,
нуль -2 и полюса -1, -5 и -10. Определить
реакцию на воздействие
.Определите воздействие
,
которое имеет следующее изображение
Лапласа
а)
б)
При построении частотных характеристик учитывают гладкость кривой, указывают на графике стрелкой направление увеличения частоты и/или крайние частоты. Построение кривой следует производить всегда по возрастанию значения частоты.
Быстрая проверка правильности расчетов:
– АФЧХ и АЧХ
начинаются при значении
;
– АФЧХ и АЧХ
заканчиваются в нуле
или в
при
.
–АФЧХ устойчивой системы, не имеющей нулей, проходит по часовой стрелке столько квадрантов, каков порядок характеристического полинома.
Пример 3. Построить АФЧХ RC–фильтра представленного на рисунке 2.1.
Рисунок 2.1
Передаточная функция фильтра имеет вид
АФЧХ фильтра запишем в виде
.
Представим это выражение в виде
.
Перед построение
АФЧХ сначала определим
и
при двух частотах
и
.
При
мы
имеем
и
,
а при
и
.
Эти точки отметим на графике (рисунок
2.2). При
имеем
и
.
АФЧХ представляет собой полуокружность с центром в точке (1/2;0) .
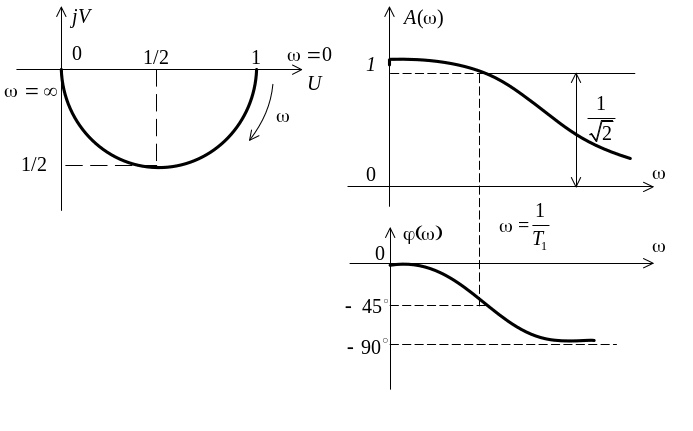
Рисунок 2.2
Упражнения:
По заданной передаточной функции найти и построить АФЧХ, АЧХ и ФЧХ.
а)
б)
в)
г)
д)
Для компьютерных дискет высокой плотности очень важно точное позиционирование головки дисковода. Система управления имеет передаточную функцию
.
Изобразить АФЧХ этой системы при
.
Вычислите модуль и аргумент
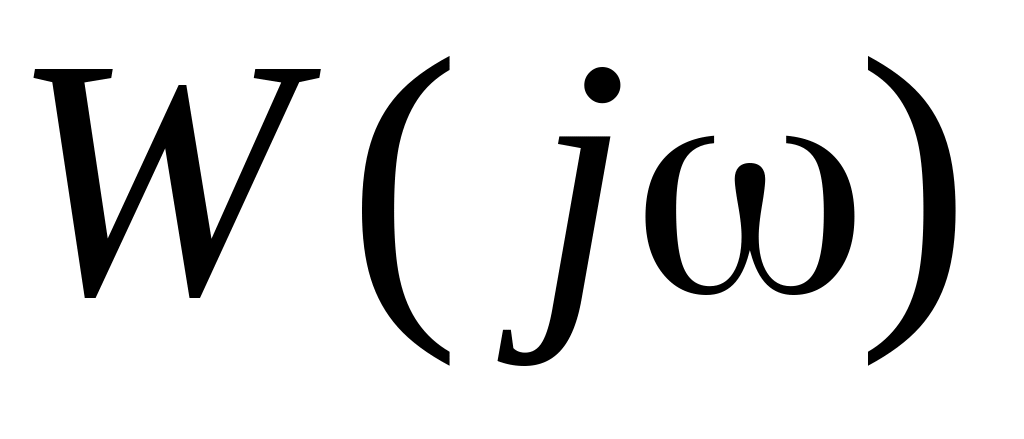при
и т.д.
Ответ:
и
.
Пример 4.
При воздействии
найти сигнал на выходе системы с
передаточной функцией
.
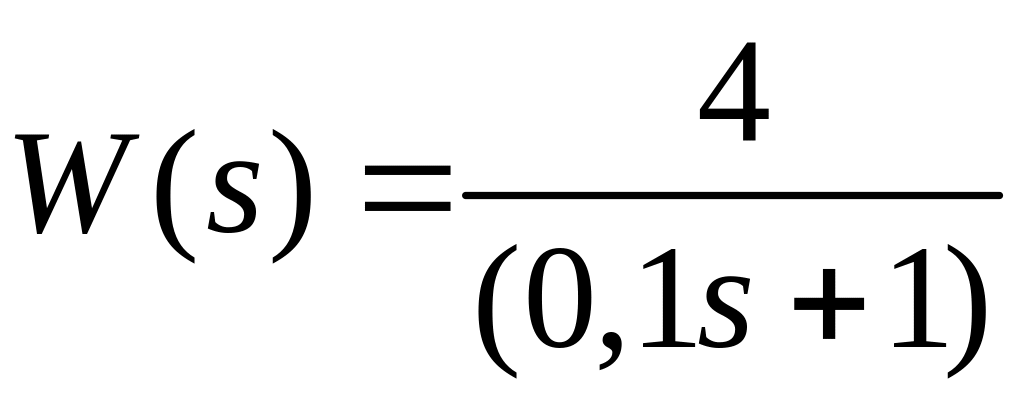По передаточной функции получим аналитическое выражение для АЧХ и ФЧХ
Для известной
частоты
рад/с
значения АЧХ и ФЧХ равны
Выражение для выходного гармонического сигнала
.
Упражнения:
Описать формулой частотную реакцию
на входное гармоническое воздействие
,
если передаточная функция фильтра
равна
.
На практике часто
применяют соответствующие логарифмические
частотные характеристики: логарифмическая
амплитудная частотная характеристика
(ЛАЧХ)
и
логарифмическая фазовая частотная
характеристика (ЛФЧХ)
,
графики которых строят в логарифмическом
масштабе.
Пример 5. Построить ЛАЧХ системы, заданной структурной схемой (рисунок 2.3).
Рисунок 2.3
Передаточная функция последовательного соединения звеньев равна
.
Определяем параметры низкочастотной (НЧ) асимптоты:
– порядок астатизма
равен
(имеется один нулевой корень в знаменателе);
– коэффициент
усиления
,
.
Через точку с
координатами (20 дБ, 1) проводим прямую с
наклоном -20 дБ/дек до сопрягающей частоты
с-1.
Поскольку сопрягающая частота соответствует звену, стоящему в знаменателе, то наклон прямой изменяется на -40 дБ/дек. График ЛАЧХ представлен на рисунке 2.4.
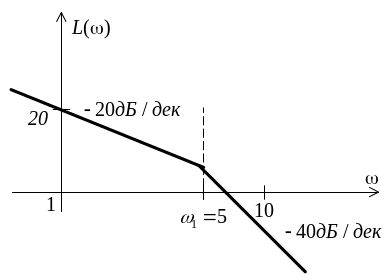
Рисунок 2.4
Упражнения:
Для передаточных функций из задания 5 представить в виде диаграмм Боле частотные характеристики.
Типичный промышленный робот имеет шесть степеней свободы. Система управления положением одного из звеньев робота имеет передаточную функцию
.
Изобразить диаграмму Боде для этой системы при .
На рисунке 2.5 изображены асимптотические амплитудные характеристики, соответствующие двум передаточным функциям. Для каждой из систем постройте соответствующую асимптотическую фазовую характеристику. Определите передаточную функцию каждой системы.
Рисунок 2.5
На рисунке 2.6 изображена амплитудная характеристика, соответствующая передаточной функции
.
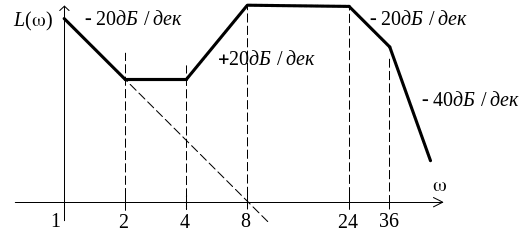
Рисунок 2.6
По этой характеристике
определите параметры
,
и
.
На рисунке 2.6 изображена схема регулирования давления в закрытой камере. Измерительный элемент имеет передаточную функцию
,
передаточная
функция вентиля
,
регулятор имеет передаточную функцию
.
а) Регулятор давления
б) Структурная схема
Рисунок 2.6
Получите логарифмическую амплитудно-частотную характеристику, соответствующую передаточной функции разомкнутого контура.
На рисунке 2.7.а) изображена структурная схема системы с обратной связью. Передаточные функции элементов системы представлены на рис.2.7. б) своими частотными характеристиками.
а)
б)
Рисунок 2.7