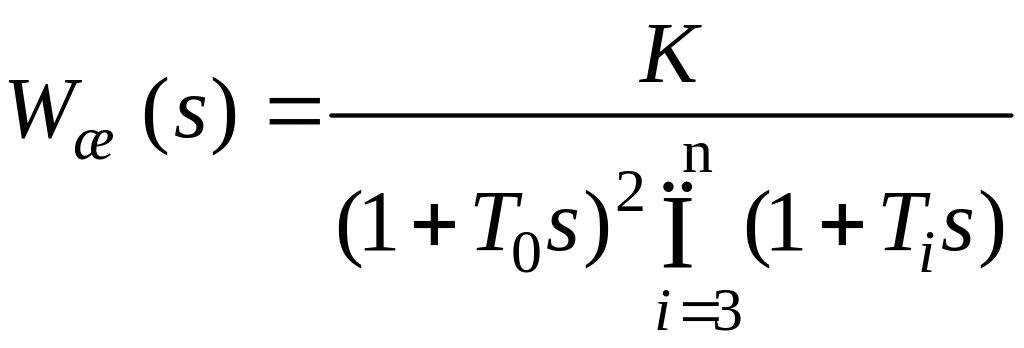4.3 Исследование управляемости и наблюдаемости сау

Рассмотрим управляемость и наблюдаемость на примере САУ второго порядка.

Если динамика САУ описывается уравнениями состояния в нормальной форме, то исследовать эти свойства системы целесообразно по матрицам управляемости и наблюдаемости.

Пример 1. Уравнения САУ имеют вид:

Определить управляемость и наблюдаемость.

Решение. Матрица

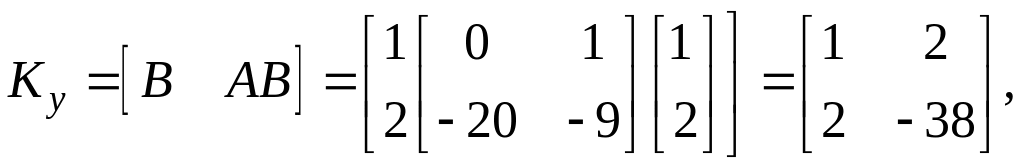
Матрица

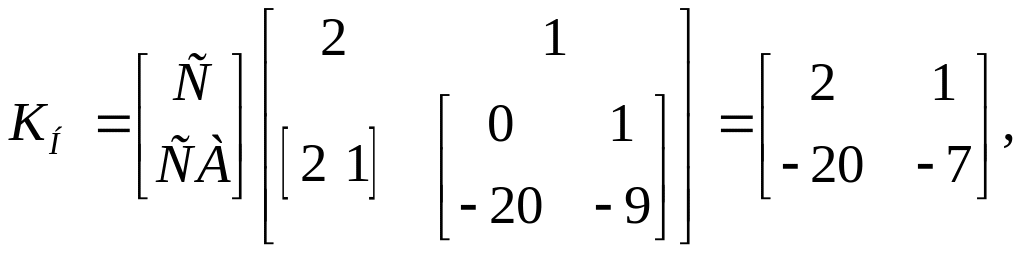
Система полностью управляема и полностью наблюдаема.

Для исследования управляемости и наблюдаемости можно перейти к канонической форме уравнений состояния и оценить матрицы В и С.

Пример 2. пусть уравнения САУ имеют вид, представленный в предыдущем примере.

Необходимо определить управляемость и наблюдаемость.

Решение. Найдем корни характеристического уравнения системы как

Модальная матрица

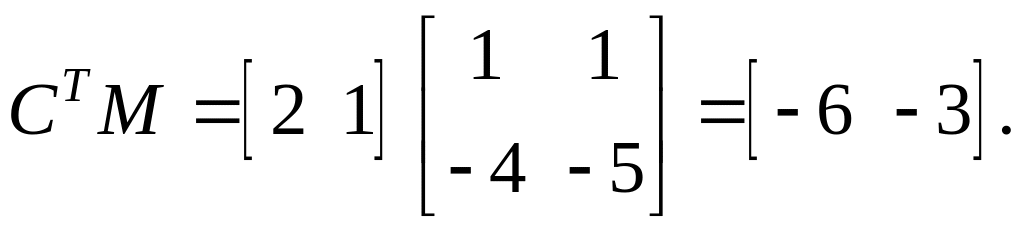
Уравнения состояния в канонической форме:

Так как матрицы и не содержат нулевых элементов, то система полностью управляема и полностью наблюдаема (выводы совпали с результатами предыдущего примера).

Упражнение:

54. сау описывается уравнениями:

Определить управляемость и наблюдаемость системы.

5 Коррекция динамических свойств

Задача коррекции состоит в том, чтобы определить передаточные функции таких корректирующих устройств, которые при минимальной сложности их реализации обеспечивают системе требуемые показатели качества.

Задачу решают в два этапа. На первом этапе осуществляют синтез желаемой передаточной функции разомкнутой системы, а на втором – выбирают наиболее предпочтительный способ коррекции и определяют передаточные функции корректирующих звеньев.

5.1 Синтез желаемой передаточной функции

Традиционные методы синтеза основаны на использовании частотных логарифмических амплитудных характеристик (ЛАХ). Наиболее часто используют типовые желаемые характеристики, приведенные в таблице 5.1.

Для всех желаемых ЛАХ характерно, что они пересекают ось нуля децибел под единичным наклоном -20 дб/дек, что необходимо для обеспечения устойчивости.

Синтез желаемой передаточной функции осуществляют в следующей последовательности. Ориентируясь на передаточную функцию разомкнутой системы, состоящей из функционально необходимых элементов, выбирают тип желаемой ЛАХ . Затем, используя заданные показатели качества, осуществляют привязку среднечастотной асимптоты с единичным наклоном к оси частот и сопрягают её с асимптотами ЛАХ неизменяемой части системы в области низких и в области высоких частот. Наконец, записывают передаточную функцию .

Методику синтеза проиллюстрируем на нескольких примерах.

Пример 1. Синтез по заданным значениям ошибки и частотного показателя качества M

Исходные данные:

Скорость изменения воздействия на входе системы с астатизмом первого порядка не превышает значения , а ускорение – . Требуется построить желаемую ЛАХ и определить системы, удовлетворяющей следующим показателям качества: максимальная ошибка , показатель колебательности . Передаточная функция исходной системы, состоящая из функционально необходимых элементов (без коррекции):

. (5.1)

Решение. Общий коэффициент разомкнутой системы . Координаты контрольной точки :

частота

; (5.2)

ордината

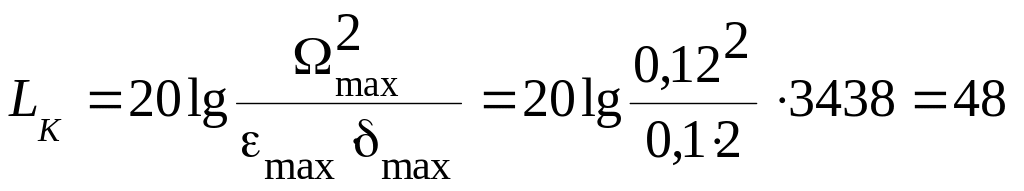дб. (5.3)

Таблица 5.1 – Типовые желаемые передаточные функции и асимптотические

ЛАХ

Передаточная функция	Асимптотическая ЛАХ

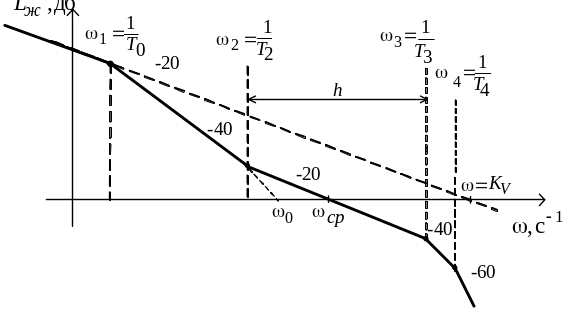
По этим данным строим запретную зону, в которую не должна попадать желаемая ЛАХ. Для этого (см. рисунок 5.1) на частоте откладываем ординату и через полученную точку проводим две прямые с наклоном -20 дб/дек и -40 дб/дек.

Рисунок 5.1

Первую сопрягающую частоту принимаем равной :

. (5.4)

Допустимое значение первой постоянной времени

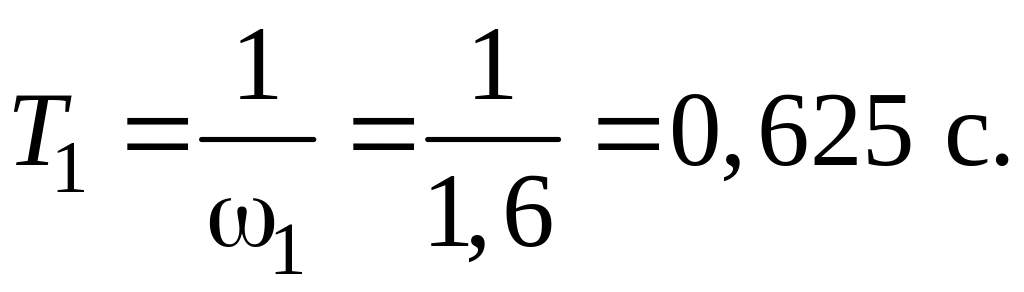(5.5)

Через точку А проводим асимптоту с наклоном -40 дб/дек и находим базовую частоту

. (5.6)

В соответствии с требованием принимаем показатель колебательности M = 1,28 и находим границы среднечастотной асимптоты:

дб, (5.7)

дб. (5.8)

Определяем частоту сопряжения как абсциссу точки В, полученной при пересечении асимптоты с наклоном -40 дб/дек верхней границы среднечастотной асимптоты:

. (5.9)

Требуемое значение второй постоянной времени

(5.10)

Строим среднечастотную асимптоту с единым наклоном до пересечения с нижней границей в точке С, абсцисса которой определяет частоту сопряжения

(5.11)

Третья постоянная времени

(5.12)

По передаточной функции (5.1) строим ЛАХ исходной системы и формируем высокочастотные асимптоты желаемой ЛАХ так, чтобы их наклоны совпадали с наклонами высокочастотных асимптот . В этом случае сопрягающая частота , а четвертая постоянная времени

(5.13)

Желаемая передаточная функция разомкнутой системы

(5.14)

Можно продолжить высокочастотный участок с наклоном -40 дб/дек до совпадения асимптот в точке D. Тогда соответствующая постоянная времени , а принимает вид

. (5.15)

Пример 2. синтез по допустимому значению установившейся ошибки и требуемым показателям качества в переходных режимах: .

Построить желаемую ЛАХ и определить передаточную функцию для системы с астатизмом первого порядка, удовлетворяющей следующим условиям: допустимое значение установившейся ошибки при постоянной скорости и ускорении ; максимальное перерегулирование ; время регулирования переходного процесса при числе колебаний ; передаточная функция исходной некорректированной системы

(5.16)

Решение. Полагаем погрешность по скорости и погрешность по ускорению равными:

(5.17)

Определяем добротности системы:

по скорости

, (5.18)

по ускорению

. (5.19)

Для дальнейших расчетов принимаем:

, , . (5.20)

Проверяем выполнение условий по точности

угл.мин. (5.21)

Условие выполняется.

Определяем первую сопрягающую частоту желаемой ЛАХ:

. (5.22)

и соответствующую ей постоянную времени Т₁ желаемой передаточной функции :

(5.23)

Принимаем . Из таблицы 3.2 находим и определяем допустимое значение частоты среза

. (5.24)

Принимаем .

Определяем вторую сопрягающую частоту

. (5.25)

и соответствующую постоянную времени

(5.26)

Строим желаемую ЛАХ до частоты среза . Через точку с ординатой дб и абсциссой проводим асимптоту с единичным наклоном -20 дб/дек до пересечения с осью абсцисс в точке . Через точку A, соответствующую частоте , проводим асимптоту с наклоном -40 дб/дек и через – асимптоту с единичным наклоном -20 дб/дек. Пересечение прямых даёт вторую опорную частоту .

Для правильного выбора параметров высокочастотной части желаемой ЛАХ построим ЛАХ исходной нескорректированной системы в соответствии с выражением (5.16). Так как наклоны высокочастотных ЛАХ и должны совпадать, то принимаем

(5.27)

и достраиваем так, как показано на рисунке 5.2.

Рисунок 5.2

Проверяем условие сохранения запасов устойчивости

, (5.28)

находим

Условие (5.28) соблюдается.

По желаемой ЛАХ записываем передаточную функцию

. (5.29)

Можно продлить среднечастотную асимптоту желаемой ЛАХ до пересечения с . Это даст новую постоянную времени и передаточную функцию

. (5.30)

Упражнения:

48 Допустимое значение ошибки по скорости угл.мин. при . Ускорение . Построить низкочастотную часть желаемой ЛАХ при следующих условиях:

а) ; б) ; в) .

Ответ: параметры низкочастотной части желаемой ЛАХ:

а) , , ;

б) , , ;

в) , , .

49 Построить среднечастотную часть желаемой ЛАХ при следующих данных:

а) , ; б) , ; в) , .

Ответ: сопрягающие частоты среднечастотной асимптоты:

а) , ;

б) , ;

в) , .

50 Построить среднечастотную часть желаемой ЛАХ, если дано: добротность системы по скорости , добротность по ускорению 180 c², максимальное перерегулирование , время регулирования переходного процесса .

Ответ: частота среза , сопрягающие частоты: , .

51 Выбрать вид желаемой ЛАХ и рассчитать параметры желаемой передаточной функции системы, которая должна обеспечивать время регулирования переходного процесса и значение ошибки по скорости при скорости изменения задающего воздействия на входе системы . Показатель колебательности системы , не более.

Примечание: при решении задачи воспользоваться соотношением .

Ответ: .