БИЛЕТ № 7 ( 22)

1. Согласно свойству сочетаний:

Б) , где

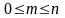
2. Несовместные события могут быть определены как:

А) несколько событий называются несовместными, если в результате опыта наступление одного из них исключает появление других;

3. Теорема умножения двух зависимых событий может быть записана как:

В)

4. Формула полной вероятности гласит:

А) если событие А может наступить только вместе с одним из событий Н_1, Н_2, Н_3,…., Н_n, образующих полную группу несовместных событий и называемых гипотезами, то вероятность события А равна сумме произведений вероятностей каждого из событий Н_1, Н_2, Н_3,…., Н_n, на соответствующую условную вероятность события А;

5. Случайную величину называют непрерывной если:

Б) она может принять любое значение из некоторого конечного или бесконечного интервала;

6. Дисперсия биномиального распределения рассчитывается как:

Б)

7. Формула распределения вероятностей Пуассона записывается как:

Б)

8. Нормальная СВ имеет плотность распределения, определяемую формулой:

А)

9. Согласно свойствам дифференциальной функции f(x),эта функция:

Б) неотрицательная;

10. Задача: вероятность сдать экзамен на право вождения автомобиля одинакова для всех слушателей курсов и равна 0,8. В группе 20 человек. Какому закону распределения будет подчиняться число слушателей, получивших права?

А) биномиальному;

11. Для расчета коэффициента асимметрии используется:

Б) центральный момент третьего порядка;

12. Средняя арифметическая постоянной величины равна:

Г)этой постоянной величине.

13. Формула простой дисперсии записывается как:

Б)

14. Серийная выборка основана на:

А) отборе случайным образом не единиц, а целых групп совокупности, которые в свою очередь подвергаются сплошному наблюдению;

15. Сущность выборочного метода состоит в том, что:

А) для изучения вместо всей совокупности элементов берётся лишь некоторая их часть, отобранная по определённым правилам;

16. Необходимый объем выборки для оценки генеральной доли при собственно- случайном бесповторном отборе может быть найден как:

Г) ;

17. Оценки параметров генеральной совокупности должны быть:

Б) несмещенными, состоятельными и эффективными;

18. Задача: в молочном отделе универсама произведено контрольное взвешивание десяти 200-грамовых пачек сливочного масла и установлено, что г. и S=4г. Менеджер отдела выдвигает предположение о недобросовестности поставщика. Прав ли он? Уровень значимости принять равным =0,001. Нулевая и альтернативная гипотезы формулируются как:

Б) ;

19. Если конкурирующая гипотеза имеет вид , то критическая область:

В) двухсторонняя;

20. Наблюдаемое значение критерия . Конкурирующая гипотеза – правосторонняя.

В) если , то нулевую гипотезу отвергают в пользу альтернативной.

Билет № 18(33)

1. Директор компании рассматривает заявления о приеме на работу 5 выпускников университета. В компании имеются три различных вакансии. Сколькими способами директор может заполнить эти вакансии? Для решения задачи нужно использовать:

В) формулу размещений

2. Теорема умножения двух независимых событий гласит, что:

В) вероятность произведения двух независимых событий А и В равна произведению их вероятностей;

3. Совместные события могут быть определены как:

Б) несколько событий называются совместными, если в результате опыта наступление одного из них не исключает появление других;

4. Вероятности гипотез, найденные по формуле Байеса называют:

Б) априорными

5. Закон распределения дискретно случайной величины может быть задан в виде:

6. Г) графика, функции и ряда распределения.

6. Математическое ожидание биномиального распределения рассчитывается как: А) ;

7. Математическое ожидание СВ, распределенной по гипергеометрическом закону А) ;:

8. Согласно свойствам функции распределения F(x), вероятность того, что НСВ примет одно определенное значение равна:

Б) нулю

9. Правило трех сигм формулируется следующим образом:

Б) если СВ распределена по нормальному закону, то ее отклонение от математического ожидания не превышает ;

10. Задача: для обнаружения некоего минерала было отправлено 6 независимых геологических экспедиций. Вероятность найти требуемый минерал оценивается как 0,05 для каждой экспедиции. Какому закону распределения подчиняется число успешных экспедиций?

А) биномиальному

11. Если значение коэффициента асимметрии , то асимметрия:

Б) несущественная левосторонняя;

12. Медиана интервального вариационного ряда может быть определена по формуле:

Б) ;

13. Средняя арифметическая взвешенная рассчитывается как:

Б) ;

14. Доверительная вероятность - это

А) вероятность того, что доверительный интервал накроет неизвестный оцениваемый параметр генеральной совокупности

15. Точечной оценкой генеральной дисперсии при объеме выборке 30 является:

Г) .

16. Средняя ошибка выборки для доли при повторном собственно – случайном отборе может быть найдена как:

В) ;

17. Теоретической основой выборочного метода является:

А) неравенство Чебышева;

18. Если проверяется нулевая гипотеза и альтернативная гипотеза правосторонняя, а уровень значимости , то критическое значение критерия:

В) ;

19. Статистическая гипотеза называется непараметрической, если в ней сформулированы предположения относительно:

А) вида закона распределения;

20. Задача: компания, выпускающая новый сорт растворимого кофе предполагает, что 50% потребителей предпочтут новый сорт кофе. Для проверки этого предположения компания провела проверку вкусов покупателей по случайной выборке из 400 человек и выяснила, что 220 из них предпочитают новый сорт кофе всем остальным. Проверьте предположение компании на уровне значимости =0,05. Нулевая и альтернативная гипотезы формулируются как:

А) ;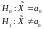