2.3. Поляризация света.

Эту тему рекомендуется изучить по §§ 134, 135, 141 учебного пособия Савельева И.В. "Курс общей физики", т.2.

Здесь рассмотрены задачи на поляризацию света при отражении и преломлении на границе двух диэлектриков, прохождение света через два поляризатора. Первая группа задач решается с помощью закона Брюстера. При решении второй группы задач нужно учитывать различное изменение интенсивности света, прошедшего через поляризатор (анализатор) в случаях, если падающий свет был естественным или плоско поляризованным.

При выполнении чертежей к решениям задач первого и второго типа нужно указать направление колебаний вектора в рассматриваемых лучах.

Пример 17. На стеклянную пластинку (n₂ = 1,6), находящуюся в жидкости, падает луч естественного света. Отраженный луч максимально поляризован и составляет угол 100° с падающим лучом. Определить скорость распространения света в жидкости.

Дано:

n₂ = 1,6

 = 100°

v₁ = ?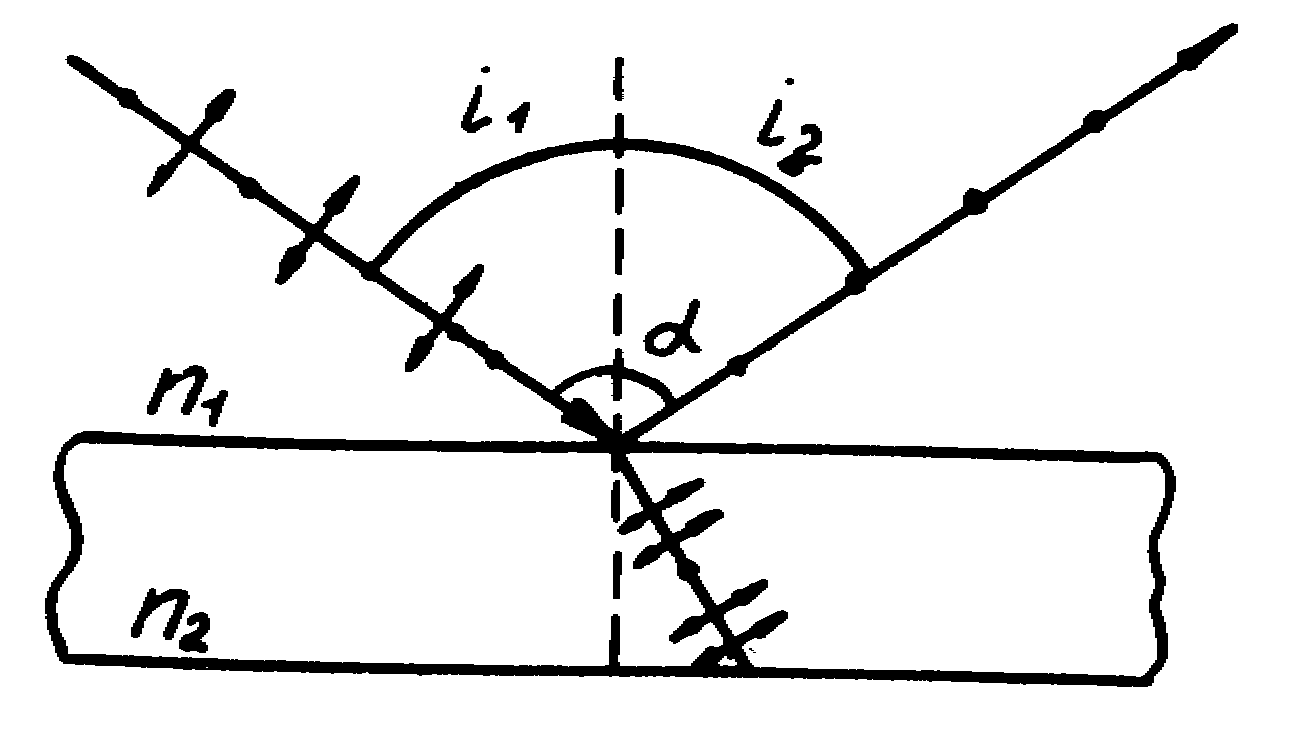

Р ешение:

На границу раздела стекло-жидкость падает естественный свет. Представим, его как суперпозицию двух волн: волну с колебаниями вектора в плоскости падения луча (на чертеже эти колебания указаны двойной стрелкой) и волну с колебаниями вектора перпендикулярно плоскости падения (на чертеже эти колебания указаны точкой).

40

По условию задачи отраженный луч полностью поляризован, т.е. он содержит колебания вектора , перпендикулярные плоскости падения, преломленный луч будет частично поляризован с преобладанием колебаний вектора в плоскости падения.

На основании закона отражения света угол падения i₁ равен углу отражения i₂, т.е.

i₁ = i₂ = .

При полной поляризации отраженного луча выполняется закон Брюстера

tgi₁ = n₂₁,

где i₁ – угол падения,

– относительный показатель преломления второй среды относительно первой ,

v₁ – скорость распространения света в первой среде (жидкость),

v₂ – скорость распространения света во второй среде(стекло),

–абсолютный показатель преломления первой среды,

–абсолютный показатель преломления второй среды,

с – скорость света в вакууме.

Отсюда

,

.

Ответ: v₁ = 2,2·10⁸ м/с.

42

Пример 18. Два николя N₁ и N₂ расположены так, что угол между их плоскостями пропускания составляет  = 60°. Определить, во сколько раз уменьшится интенсивность I₀ естественного света: 1) при прохождении через один николь N₁, 2) при прохождении через оба николя. Коэффициент поглощения света в николе k = 0,05. Потери при отражение света не учитывать.

Дано:

 = 60°

k = 0,05

Р ешение:

1) Естественный свет, падая на грань призмы Николя, расщепляется вследствие двойного лучепреломления на два луча: обыкновенный и необыкновенный. Оба луча одинаковы по интенсивности и полностью поляризованы. Плоскость колебаний необыкновенного луча лежит в плоскости чертежа (плоскость главного сечения). Плоскость колебаний обыкновенного луча перпендикулярна плоскости чертежа. Обыкновенный луч света (о) вследствие полного отражения от границы АВ отбрасывается на зачерненную поверхность призмы и поглощается ею. Необыкновенный луч (е) проходит через призму, уменьшая свою интенсивность вследствие поглощения. Таким образом, интенсивность света, проведшего через первую призму,

.

Относительное уменьшение интенсивности света получим, разделив интенсивность I₀ естественного света, падающего на первый николь, на интенсивность I₁ поляризованного света:

. (1)

Таким образом, интенсивность уменьшается в 2,1 раза.

43

2) Плоско поляризованный луч света интенсивности I₁ падает на второй николь N₂ и также расщепляется на два луча различной интенсивности: обыкновенный и необыкновенный. Обыкновенный луч полностью поглощается призмой, поэтому интенсивность его нас не интересует. Интенсивность I₂ необыкновенного луча, вышедшего из призмы N₂, определяется законом Малюса (без - учета поглощения света во втором николе):

I₂ = I₁cos²,

угол  – это угол между плоскостью колебаний в поляризованном луче и плоскостью пропускания николя N₂.

Учитывая потери интенсивности на поглощение во втором николе, получаем

I₂ = I₁(1-k)cos².

Искомое уменьшение интенсивности при прохождении света через оба николя найдем, разделив интенсивность I₀ естественного света на интенсивность I₂ света, прошедшего систему из двух николей:

,

Заменяя отношение его выражением по формуле (1), получаем

,

Произведём вычисления:

.

Таким образом, после прохождения света через два николя интенсивность его уменьшается в 8,86 раза.

Ответ: 1) 2) .

44