1.2. Сложение колебаний.

Рекомендуется изучить §§ 55-57 учебного пособия И.В. Савельева "Курс общей физики" т. 1. М. Наука, 1982 г.

При сложении двух одинаково направленных гармонических колебаний одинакового периода

,

получается гармоническое колебание того же периода

,

амплитуда А и начальная фаза  которого определяется уравнениями:

,

,

где А₁ и А₂ – амплитуды слагаемых колебаний,

₁ и ₂ - начальные фазы слагаемых колебаний.

П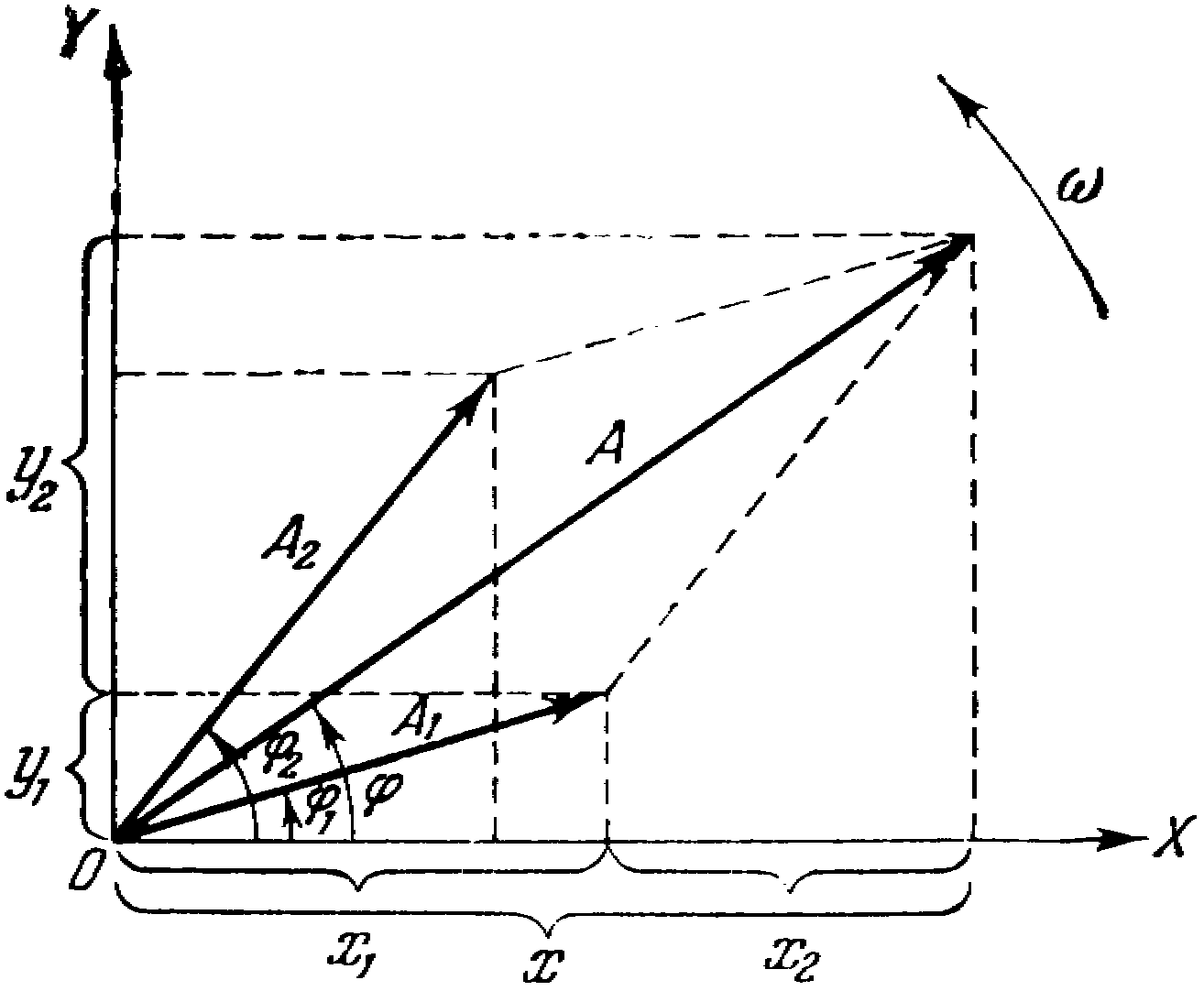 ри сложении N (N > 2) одинаково направленных гармонических колебаний равных периодов, амплитуду и начальную фазу результирующего колебания можно находить применяя метод векторных диаграмм.

В результате задач такого типа необходимо получить вид функций, описывающих изменение смещения (для контура q, u), скорости (для контура i), ускорения.

В задачах на определение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях, следует исключить время из уравнений складываемых колебаний и найти уравнение, которое описывает результирующее колебание.

16

Пример 5. Найти амплитуду и начальную фазу гармонического колебания, полученного при сложении двух гармонических колебаний одинакового направления и одинаковой частоты, уравнения которых м и м. Написать уравнение результирующего колебания.

Дано:

x(t) = ?

Решение:

Согласно принципу суперпозиции:

x  x₁ +x₂.

Сложение колебаний произведем методом векторной диаграммы. Для этого, используя тригонометрическую формулу приведения

,

уравнения складываемых колебаний выразим через функцию косинуса и запишем их в канонической форме:

,

.

Построим векторную диаграмму (см. стр. 16) для t  0. Учтем, что A₁  0,02 м, A₂  0,03 м, , .

Результирующее колебание имеет ту же частоту    и амплитуду , которая равна геометрической сумме амплитуд складываемых колебаний

 + .

Согласно теореме косинусов:

A .

17

Начальная фаза результирующего колебания:

.

Представим числовые значения и произведем вычисления:

A   0,05 м,

.

Уравнение результирующего колебания:

x  0,05cos(t  0,23).

Ответ: x  0,05cos(t  0,23) м.

Пример 6. Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями x  cost и y  cos . Определить уравнение траектории точки и построить ее на чертеже, показав направление движения точки.

Дано:

x  cost

y  cos

y = f(x)

Решение:

По условию задачи:

x  ,

y  ,

т.е. A₁  A₂  1, ₁  2₂.

Для определения уравнения траектории точки необходимо найти связь между y и x, исключив время t. Применим формулу косинуса кратных углов:

cos2  cos² – sin²  1 – 2sin² = 2cos² – 1.

Используя это соотношение , можно написать:

cost  .

Учитывая заданные уравнения, получим:

x  2y² – 1.

18

.

Полученное уравнение представляет собой параболу, у которой ось лежит на оси 0x, ветви направлены в положительном направлении оси 0х.

Траектория результирующего колебания точки представляет собой часть параболы, заключенной внутри прямоугольника амплитуд со сторонами 2A₁, 2A₂.

Для построения траектории найдем значения y, соответствующие ряду значений x.

х	–1	0	1
у	0		±1

Определим направление движения.

В начальный момент при t  0 имеем: x  1, y  1. Точка находится в положении а.

При t  1 с получим x  – 1, y  0. Материальная точка находится в вершине параболы b.

При t  2 с получим x  1, y  – 1. Материальная точка находится в положении c.

П осле этого она будет двигаться в обратном направлении.

Ответ: .

19