45. Методы расчётов переходных процессов в нелинейных цепях.

Переходные  процессы  в  нелинейных  электрических  цепях  описываются  нелинейными дифференциальными уравнениями,  общих  методов интегрирования которых не существует.  На  нелинейные  цепи не распространяется принцип суперпозиции, поэтому основанные на нем методы, в частности классический или с использованием интеграла Дюамеля, для расчета данных цепей не применимы.

Анализ переходных режимов в электрических цепях требует использования динамических характеристик нелинейных элементов, которые, в свою очередь, зависят от происходящих в них динамических процессов и, следовательно, в общем случае наперед неизвестны. Указанное изначально обусловливает в той или иной степени приближенный характер расчета переходных процессов.

Переходный процесс в нелинейной цепи может характеризоваться переменной скоростью его протекания в различные интервалы времени. Поэтому понятие постоянной времени в общем случае не применимо для оценки интенсивности протекания динамического режима.

Отсутствие общности подхода к интегрированию нелинейных дифференциальных уравнений обусловило наличие в математике большого числа разнообразных методов их решения, нацеленных на различные типы уравнений. Применительно к задачам электротехники все методы расчета по своей сущности могут быть разделены на три группы:

– аналитические методы, предполагающие либо аналитическое выражение характеристик нелинейных элементов, либо их кусочно-линейную аппроксимацию;

– графические методы, основными операциями в которых являются графические построения, часто сопровождаемые вспомогательными вычислительными этапами;

– численные методы, основанные на замене дифференциальных уравнений алгебраическими для приращений переменных за соответствующие интервалы времени.

46. Временные характеристики лэц. Импульсная характеристика, её виды и размерность. Способы определения g(t)

Максимальное значение - .

Действующее значение - .

Среднее по модулю значение - .

Среднее за период значение (постоянная составляющая) - .

Коэффициент амплитуды (отношение максимального значения к действующему) - .

Коэффициент формы (отношение действующего значения к среднему по модулю) - .

Коэффициент искажений (отношение действующего значения первой гармоники к действующему значению переменной) - .

Коэффициент гармоник (отношение действующего значения высших гармонических к действующему значению первой гармоники) - .

Импульсная характеристика (функция) - это реакция системы на входное единичное импульсное воздействие при нулевых начальных условиях.

Дельта-функция обладает следующими свойствами:

(2.9)

С помощью дельта-функции моделируется реальное входное воздействие типа удара.

Рис.2.5. Импульсная характеристика системы

Примеp 2.5:

Импульсные характеристики для различных значений активного сопротивления в электрической цепи:

Импульсная функция позволяет вычислить реакцию системы на произвольное входное воздействие при нулевых начальных условиях по выражению

(2.10)

Переходная функция и импульсная функция однозначно связаны между собой соотношениями

(2.11)

что позволяет по одной известной характеристике определить вторую.

47. Дифференцирующие цепи. Требования к дифференцирующим цепям в частотной и временной областях.

ДИФФЕРЕНЦИРУЮЩАЯ ЦЕПЬ - устройство, предназначенное для дифференцирования по времени электрич. сигналов. Выходная реакция Д. ц. u_вых(t) связана со входным воздействием u_вх(t) соотношением   , где  - пост. величина, имеющая размерность времени. Различают пассивные и активные Д. ц. Пассивные Д. ц. применяют в импульсных и цифровых устройствах для укорачивания импульсов. Aктивные Д. ц. используют как дифференциаторы в аналоговых вычислит. устройствах. Простейшая пассивная Д. ц. показана на рис. 1, а. Ток   через ёмкость пропорционален производной приложенного к ней напряжения   . Если параметры Д. ц. выбраны т. о.,

что u_c=u_вх, то   , a  . Условие u_c=u_вх выполняется, если на самой верхней частоте  спектра входного сигнала   Вариант пассивной Д. ц. показан на рис. 1, б. При условии   имеем   и

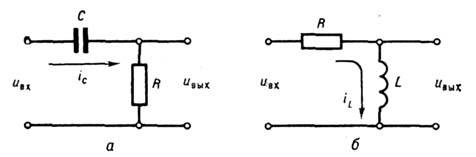
Рис. 1. Схемы пассивных дифференцирующих цепей: а - ёмкостной RC; б - индуктивной RL.

Следовательно, при заданных параметрах Д. ц. дифференцирование тем точнее, чем ниже частоты, на к-рых концентрируется энергия входного сигнала. Однако чем точнее дифференцирование, тем меньше коэфф. передачи цепи и, следовательно, уровень выходного сигнала. Это противоречие устраняется в активных Д. ц., где процесс дифференцирования сочетается с процессом усиления. В активных Д. ц. используют операционные усилители (ОУ), охваченные отрицательной обратной связью (рис. 2). Входное напряжение u_вх(t) дифференцируется цепочкой, образованной последоват. соединением ёмкости С и R_экв - эквивалентного сопротивления схемы между зажимами 2-2', а затем усиливается ОУ. Если подать напряжение на инвертирующий вход ОУ, то при условии, что его коэффициент усиления   ,  , получим

.

Рис. 2. Схема активной дифференцирующей цепи.

Рис. 3. Прохождение импульса через дифференцирующую цепь RC: а - входной импульс, u_вх=Е при   ; б - напряжение на ёмкости u_c(t); в- выходное н апряжение  .

Для сравнит. оценки активных и пассивных Д. ц. при прочих равных условиях можно использовать отношение   . При прохождении через Д. ц. импульсных сигналов происходит уменьшение их длительности, отсюда понятие о Д. ц. как об укорачивающих. Временные диаграммы, иллюстрирующие прохождение импульса прямоугольной формы через пассивную Д. ц., приведены на рис. 3. Предполагается, что , источник входного напряжения характеризуется нулевым внутр. сопротивлением, а Д. ц.- отсутствием паразитных ёмкостей. Наличие внутр. сопротивления приводит к уменьшению амплитуды напряжения на входных клеммах и, следовательно, к уменьшению амплитуд выходных импульсов; наличие паразитных ёмкостей - к затягиванию процессов нарастания и спада выходных импульсов. Аналогичным укорачивающим действием обладают также активные Д. ц.