
- •Основы подземной гидромеханики
- •Введение
- •1.Дифференциальные уравнения фильтрации
- •1.1.Основные понятия и определения
- •1.2.Закон Дарси
- •1.3.Нарушение закона Дарси. Нелинейные законы фильтрации
- •1.4.Уравнение неразрывности потока
- •1.5.Зависимость параметров жидкости, газа и пористой среды от давления
- •1.6.Начальные и граничные условия
- •Пример 1.1.
- •Пример 1.2.
- •Пример 1.3.
- •Пример 1.4.
- •Пример 1.5.
- •2.Установившееся движение несжимаемой жидкости по закону Дарси
- •2.1.Дифференциальные уравнения установившегося движения
- •2.1.1.Плоскопараллельный поток (приток к галереи)
- •2.1.2.Плоскорадиальный поток (приток к скважине)
- •2.1.3.Исследование нефтяных скважин на стационарных режимах. Индикаторные диаграммы
- •2.2.Фильтрация в слоистых и зонально-неоднородных пластах
- •2.2.1.Приток к скважине и галерее в неоднородном по толщине пласте
- •2.2.2.Приток к скважине в зонально-неоднородном пласте
- •2.2.3.Приток к галерее в зонально–неоднородном пласте
- •2.3.Приток к несовершенным скважинам
- •2.4.Примеры и задачи Пример 2.6.
- •Пример 2.7.
- •Пример 2.8.
- •Пример 2.9.
- •Пример 2.10.
- •Пример 2.11.
- •3.Установившееся движение сжимаемой жидкости и газа
- •3.1.Дифференциальные уравнения установившегося движения упругой жидкости
- •3.2.Приток газа к скважине по закону Дарси
- •3.3.Исследование газовых скважин на стационарных режимах
- •3.4.Плоскорадиальный поток идеального газа при нарушении закона Дарси
- •3.5.Исследование газовых скважин на стационарных режимах при нарушении закона Дарси
- •3.6.Примеры и задачи
- •Пример 3.13.
- •Пример 3.14.
- •4.Интерференция скважин
- •4.1.Приток жидкости к группе скважин с удаленным контуром питания
- •4.2.Приток к скважине, расположенной вблизи прямолинейной непроницаемой границы
- •4.3.Приток к скважине в пласте с прямолинейным контуром питания
- •4.4.Приток к бесконечным цепочкам и кольцевым батареям скважин
- •4.5.Примеры и задачи Пример 4.16.
- •5.Контрольные задания
- •Вопросы к контрольной работе
- •6.Список использованной литературы:
- •7.Приложение
- •Оглавление
- •1. Дифференциальные уравнения фильтрации 4
- •2. Установившееся движение несжимаемой жидкости по закону Дарси 26
- •3. Установившееся движение сжимаемой жидкости и газа 55
3.2.Приток газа к скважине по закону Дарси
Исследуем установившийся плоскорадиальный фильтрационный поток идеального газа. Для этого воспользуемся аналогией между фильтрацией несжимаемой жидкости и газа. Запишем формулу дебита совершенной скважины для несжимаемой жидкости:
|
(3.0) |
Произведем в этом уравнении замены. Заменим давление p на функцию Лейбензона P, а объемный расход Q на массовый расход Qm.
|
(3.0) |
В последней формуле распишем функцию Лейбензона, тогда массовый дебит газовой скважины будет рассчитываться по формуле:
|
(3.0) |
а приведенный к атмосферным условиям объемный расход
|
(3.0) |
Расчет распределения давления вокруг газовой скважины производится в той же последовательности:
|
(3.0) |
Скорости фильтрации в любой точки вокруг скважины можно найти из уравнения неразрывности:
|
(3.0) |
На Рис. 3 .19.a, и b приведены распределение давления и скорости фильтрации вокруг газовой скважины. У газовой скважины падение давления вблизи скважины больше, чем у нефтяной, поэтому при прочих равных условиях и скорости фильтрации у газовой скважины уменьшается быстрее, чем у нефтяной скважины.
Рис. 3.19. |
3.3.Исследование газовых скважин на стационарных режимах
Исследование газовых скважин на стационарных режимах производятся аналогично исследованию нефтяных скважин. На каждом режиме (определенном диаметра отверстия штуцера) замеряют дебит газовой скважины Qат и давление на скважине pc. Если скважина закрыта, то давление в горизонтальном пласте одинаково и равно давлению на контуре питания, а дебит скважины равен нулю. По результатам исследований строят индикаторную диаграмму. Индикаторной диаграммой для газовой скважины называют зависимость разности квадратов абсолютных давлений от дебита скважины. Поэтому по известным давлениям на скважине и контурному давлению (давлению на забое закрытой скважине) находят Δp2 = pk2 - pс2 и строят график зависимости Δp2 = Δp2(Qат). Характерные типы индикаторных диаграмм приведены на Рис. 3.4.
Рис. 3.20. |
Для определения параметров пласта необходимо по точкам при малых расходах провести прямую линии проходящую через начало координат. На этой линии выбрать любую точку и найти значения Δp2* и Q*. По этим значениям найти коэффициент продуктивности газовой скважины K, который является отношением дебита скважины к разности квадратов давлений
|
(3.0) |
и имеет размерность м3/(с·Па2). Величина обратная коэффициенту продуктивности называется фильтрационным сопротивлением
|
(3.0) |
Для газовых скважин при фильтрации по закону Дарси коэффициент продуктивности равен
|
(3.0) |
По известному значению коэффициента продуктивности или фильтрационного сопротивления можно найти гидропроводность пласта kh/μ
|
(3.0) |

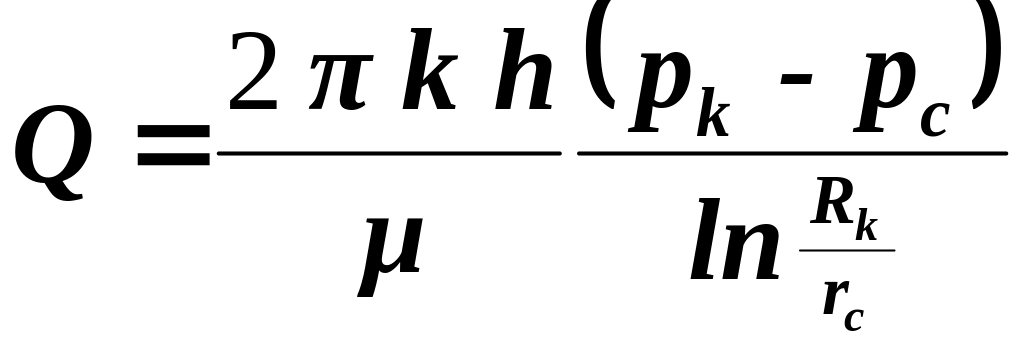 .
. .
.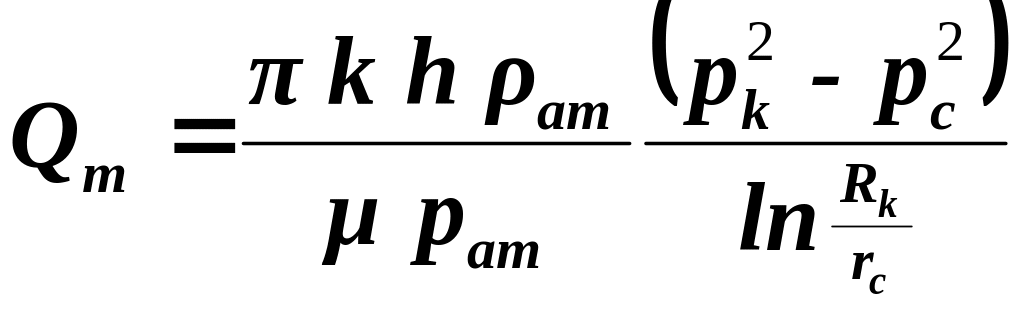 ,
, .
.
 Распределение давления a)
и отношение скорости фильтрации в
пласте к скорости фильтрации на
скважине б) для газовой скважины
Распределение давления a)
и отношение скорости фильтрации в
пласте к скорости фильтрации на
скважине б) для газовой скважины Индикаторные диаграммы газовых скважин
Индикаторные диаграммы газовых скважин