
- •Основы подземной гидромеханики
- •Введение
- •1.Дифференциальные уравнения фильтрации
- •1.1.Основные понятия и определения
- •1.2.Закон Дарси
- •1.3.Нарушение закона Дарси. Нелинейные законы фильтрации
- •1.4.Уравнение неразрывности потока
- •1.5.Зависимость параметров жидкости, газа и пористой среды от давления
- •1.6.Начальные и граничные условия
- •Пример 1.1.
- •Пример 1.2.
- •Пример 1.3.
- •Пример 1.4.
- •Пример 1.5.
- •2.Установившееся движение несжимаемой жидкости по закону Дарси
- •2.1.Дифференциальные уравнения установившегося движения
- •2.1.1.Плоскопараллельный поток (приток к галереи)
- •2.1.2.Плоскорадиальный поток (приток к скважине)
- •2.1.3.Исследование нефтяных скважин на стационарных режимах. Индикаторные диаграммы
- •2.2.Фильтрация в слоистых и зонально-неоднородных пластах
- •2.2.1.Приток к скважине и галерее в неоднородном по толщине пласте
- •2.2.2.Приток к скважине в зонально-неоднородном пласте
- •2.2.3.Приток к галерее в зонально–неоднородном пласте
- •2.3.Приток к несовершенным скважинам
- •2.4.Примеры и задачи Пример 2.6.
- •Пример 2.7.
- •Пример 2.8.
- •Пример 2.9.
- •Пример 2.10.
- •Пример 2.11.
- •3.Установившееся движение сжимаемой жидкости и газа
- •3.1.Дифференциальные уравнения установившегося движения упругой жидкости
- •3.2.Приток газа к скважине по закону Дарси
- •3.3.Исследование газовых скважин на стационарных режимах
- •3.4.Плоскорадиальный поток идеального газа при нарушении закона Дарси
- •3.5.Исследование газовых скважин на стационарных режимах при нарушении закона Дарси
- •3.6.Примеры и задачи
- •Пример 3.13.
- •Пример 3.14.
- •4.Интерференция скважин
- •4.1.Приток жидкости к группе скважин с удаленным контуром питания
- •4.2.Приток к скважине, расположенной вблизи прямолинейной непроницаемой границы
- •4.3.Приток к скважине в пласте с прямолинейным контуром питания
- •4.4.Приток к бесконечным цепочкам и кольцевым батареям скважин
- •4.5.Примеры и задачи Пример 4.16.
- •5.Контрольные задания
- •Вопросы к контрольной работе
- •6.Список использованной литературы:
- •7.Приложение
- •Оглавление
- •1. Дифференциальные уравнения фильтрации 4
- •2. Установившееся движение несжимаемой жидкости по закону Дарси 26
- •3. Установившееся движение сжимаемой жидкости и газа 55
Пример 2.8.
Таблица 2.1 |
||
Q, м3/сут |
Pмс, МПа |
p, МПа |
0 |
49,9 |
0 |
8,6 |
48,8 |
1,1 |
17,2 |
47,9 |
2 |
25,9 |
46,8 |
3,1 |
34,5 |
45,9 |
4 |
40,2 |
44,8 |
5,1 |
Решение:
Рис. 2.17. |
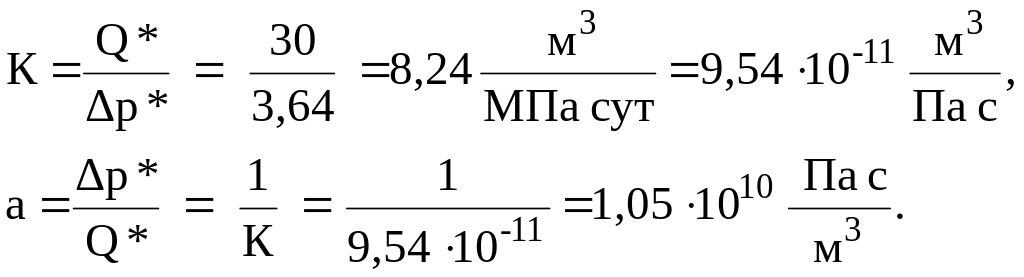 фильтрационного
сопротивления a:
фильтрационного
сопротивления a:
По значению фильтрационного сопротивления находим коэффициент гидропроводности пласта и проницаемость пласта:

Более точно параметры пласта можно найти обработав результаты исследования методом наименьших квадратов.
Ответ: k = 2,62 10-13 м2.
Пример 2.9.
Неоднородный по толщине нефтяной пласт состоит из трех пропластков, которые имеют толщины 3,6; 0,4; 6 метров и имеют проницаемости 0,05; 0,3; 0,1 мкм2. Пласт вскрыт скважиной радиусом 0,1 м и расстоянием да контура питания 250 м. Давления на контуре питания и скважине равны pк = 35 МПа и pс = 18 МПа. Динамическая вязкость пластовой нефти μн = 25 мПа·с, а пластовой воды μв = 1,2 мПа·с.
Определить:
среднюю проницаемость пласта;
дебит скважины;
обводненность скважины, если обводнится высокопроницаемый пропласток.
Решение:
Вся толщина пласта равна сумме толщин пропластков
h = h1 + h2 + h3 = 3,6 + 0,4 + 6 = 10 м.
Средняя проницаемость неоднородного по толщине пласта и для скважины и для галереи определяется по формуле:
![]() .
.
Дебит скважины рассчитывается по формуле однородного пласта, в которой проницаемость пласта заменена на среднюю проницаемость
 Пронумеруем
пропластки сверху вниз. В этом случае
самым высокопроницаемым пропластком
является второй пропласток. Именно этот
пропласток обводнится первым и именно
по этому пропласту пойдет вода, дебит
которой равен
Пронумеруем
пропластки сверху вниз. В этом случае
самым высокопроницаемым пропластком
является второй пропласток. Именно этот
пропласток обводнится первым и именно
по этому пропласту пойдет вода, дебит
которой равен
 .
.
Остальные два пропластка будут давать нефть. Дебит нефти равен сумме дебитов по пропласткам
 .
.
Коэффициентом обводненности скважины называется отношение дебита воды к дебиту жидкости

Как видно из расчетов, хотя большая часть пласта по толщине (9,6 м) занята нефтью, обводненность скважины в этом примере равна 76%.
Ответ: kср = 0,09 10-12 м2; Q = 4,91 10-4 м3/с; ν = 76%.

 Обработка результатов исследования
нефтяной скважины на стационарных
режимах
Обработка результатов исследования
нефтяной скважины на стационарных
режимах