
- •Практическая часть. Вариант 2. Статистические методы анализа численности состава населения.
- •Данные обследования населения поселка в возрасте 20-40 лет
- •Кумулята.
- •Распределение жителей поселка по возрасту и доходу.
- •1) По средней арифметической простой.
- •2) По средней арифметической взвешенной.
- •6. Определить модальные и медианные значения дохода жителей: а) по несгруппированным данным; б) из статистического ряда распределения (пункт 1) аналитически и графически.
- •Список используемой литературы.
6. Определить модальные и медианные значения дохода жителей: а) по несгруппированным данным; б) из статистического ряда распределения (пункт 1) аналитически и графически.
Решение:
А) Определим модальные и медианные значения дохода жителей по несгруппированным данным.
Мода-это значение признака, имеющее наибольшую частоту.
![]()
Медианна – середина ранжированного ряда.
13,4 |
13,6 |
13,7 |
13,8 |
14,2 |
14,9 |
15,1 |
15,4 |
15,8 |
15,9 |
15,9 |
15,9 |
16 |
16,2 |
16,2 |
16,2 |
16,2 |
16,4 |
16,5 |
16,6 |
16,7 |
16,7 |
16,8 |
16,8 |
16,9 |
17,3 |
17,4 |
17,4 |
17,6 |
17,7 |
17,8 |
18,1 |
18,3 |
18,4 |
18,9 |
19,6 |
19,6 |
19,6 |
19,6 |
21,4 |
![]()
Б) Определим модальные и медианные значения дохода жителей из статистического ряда распределения (пункт 1) аналитически и графически.
Доход жителей |
Частоты |
|
простые |
накопленные |
|
13,4-14,7 |
5 |
5 |
14,7-16,0 |
8 |
13 |
16,1-17,4 |
15 |
28 |
17,5-18,8 |
6 |
34 |
18,8-20,1 |
5 |
39 |
20,1-21,4 |
1 |
40 |
Модальным является интервал 3, т.к. он имеет наибольшую частоту.
Определим моду по следующей формуле:
![]() ,
где
,
где
Х0 – нижняя граница модального интервала;
i – величина модального интервала;
![]() - частота модального интервала;
- частота модального интервала;
![]() - частота интервала, предшествующего
модальному;
- частота интервала, предшествующего
модальному;
![]() - частота интервала, следующего за
модальным.
- частота интервала, следующего за
модальным.
![]()
Определим медиану последующей формуле:
![]() , где
, где
Х0 – нижняя граница медианного интервала;
i – частота медианного интервала;
f - частота i-ого интервала;
![]() - суммарная частота;
- суммарная частота;
![]() - накопленная частота интервалов,
предшествующего медианному;
- накопленная частота интервалов,
предшествующего медианному;
![]() - частота медианного интервала.
- частота медианного интервала.
40/2=20 – половина общей суммы частот.
Медианный интервал – 3, т.к. это первый интервал, накопленная частота которого, превышает половину общей суммы частот.
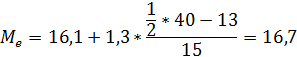
Графическое построение моды и медианы.
Графически мода определяется по гистограмме. Вершины самого высокого прямоугольника (модального) соединяются с близлежащими ему вершинами многоугольника диагональю. Из точки их пересечения опускают перпендикуляр на ось абсцисс. Полученное значение – мода.
Графически медиана определяется по кумуляте. Для этого из точки на оси ординат равной половине накопленных частот, проводят прямую параллельную оси абсцисс до пересечения с кумулятой. Проекция точки пересечения на ось абсцисс и даст медиану.
Построим графически моду и медиану:
7. Приняв данные таблицы 1 как результат 5%-ного выборочного обследования жителей поселка, определить среднюю ошибку выборки для среднего дохода жителей. Указать с вероятностью 0,954 пределы возможных значений этих показателей в генеральной совокупности для повторного и бесповторного отбора.
Решение:
По данным задания №5 (несгруппированным данным) возьмем необходимые показатели:
=3,3
=16,8
1) Определим среднюю ошибку выборки для среднего дохода жителей (для повторного отбора).
![]() ,
t=2,
т.к. согласно теореме Ляпунова при t=2,
величина
,
t=2,
т.к. согласно теореме Ляпунова при t=2,
величина ![]() не превышает двух величин средней ошибки
выборки и равна 0,954 или 95,4%
не превышает двух величин средней ошибки
выборки и равна 0,954 или 95,4%
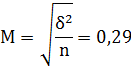
![]()
16,8 - 0,57<=![]() <=16,8+0,57
<=16,8+0,57
16,23 17,37
Ответ: при среднем доходе жителей равному в выборке 16,8 тыс . рублей среднее его значение в генеральной совокупности будет находиться в пределах от 16,23 до 17,37 тыс. рублей и вероятность этого составит 95,4%.
2) Определим среднюю ошибку выборки для среднего дохода жителей (для бесповторного отбора).
, t=2, т.к. согласно теореме Ляпунова при t=2, величина не превышает двух величин средней ошибки выборки и равна 0,954 или 95,4%
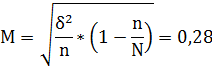
![]()
16,8 - 0,56<= <=16,8+0,56
16,24 17,36
Ответ: при среднем доходе жителей равному в выборке 16,8 тыс . рублей среднее его значение в генеральной совокупности будет находиться в пределах от 16,24 до 17,36 тыс. рублей и вероятность этого составит 95,4%.
8. Вычислить параметры линейного уравнения регрессии для зависимости дохода жителей от их возраста. Определить тесноту связи между признаками с помощью коэффициента корреляции знаков (коэффициента Фехнера).
Решение:
Необходимые расчеты произведем в таблице 2.
Y=a+bx – линейное уравнение регрессии.
![]()
С помощью данной системы уравнений при известных х и у определим a и b линейного уравнения парной регрессии.
a=15,3
b=0,05
Получаем линейное уравнение регрессии:
Y=15,3+0,05x
![]() %
%
![]()
Ответ: т.к. Кф =-0,05, т.е. близок к -1, можно сделать вывод о том, что связь обратная или близкая к ней.
Таблица 2
|
|
|
|
|
|
знак отклонения |
|
|
|
№ п/п |
xi |
yi |
xy |
x^2 |
Yсред |
xi-xcр |
yi-yср |
nc |
nH |
1 |
37 |
13,8 |
510,6 |
1369 |
17,15 |
1 |
0 |
|
н |
2 |
39 |
19,6 |
764,4 |
1521 |
17,25 |
1 |
1 |
с |
|
3 |
21 |
13,4 |
281,4 |
441 |
16,35 |
0 |
0 |
с |
|
4 |
20 |
17,7 |
354 |
400 |
16,3 |
0 |
1 |
|
н |
5 |
25 |
14,2 |
355 |
625 |
16,55 |
0 |
0 |
с |
|
6 |
29 |
13,7 |
397,3 |
841 |
16,75 |
0 |
0 |
c |
|
7 |
36 |
14,9 |
536,4 |
1296 |
17,1 |
1 |
0 |
|
н |
8 |
28 |
19,6 |
548,8 |
784 |
16,7 |
0 |
1 |
|
н |
9 |
24 |
16,2 |
388,8 |
576 |
16,5 |
0 |
0 |
с |
|
10 |
26 |
16,5 |
429 |
676 |
16,6 |
0 |
0 |
с |
|
11 |
38 |
17,4 |
661,2 |
1444 |
17,2 |
1 |
1 |
с |
|
12 |
33 |
17,6 |
580,8 |
1089 |
16,95 |
1 |
1 |
с |
|
13 |
40 |
16,4 |
656 |
1600 |
17,3 |
1 |
0 |
|
н |
14 |
40 |
16 |
640 |
1600 |
17,3 |
1 |
0 |
|
н |
15 |
23 |
15,8 |
363,4 |
529 |
16,45 |
0 |
0 |
с |
|
16 |
21 |
15,9 |
333,9 |
441 |
16,35 |
0 |
0 |
с |
|
17 |
27 |
17,8 |
480,6 |
729 |
16,65 |
0 |
1 |
|
н |
18 |
25 |
15,9 |
397,5 |
625 |
16,55 |
0 |
0 |
с |
|
19 |
33 |
17,3 |
570,9 |
1089 |
16,95 |
0 |
1 |
|
н |
20 |
35 |
17,4 |
609 |
1225 |
17,05 |
0 |
1 |
|
н |
21 |
22 |
16,6 |
365,2 |
484 |
16,4 |
0 |
0 |
с |
|
22 |
38 |
15,4 |
585,2 |
1444 |
17,2 |
1 |
0 |
|
н |
23 |
30 |
15,9 |
477 |
900 |
16,8 |
1 |
0 |
|
н |
24 |
24 |
16,2 |
388,8 |
576 |
16,5 |
0 |
0 |
с |
|
25 |
33 |
18,9 |
623,7 |
1089 |
16,95 |
1 |
1 |
с |
|
26 |
22 |
13,6 |
299,2 |
484 |
16,4 |
0 |
0 |
с |
|
27 |
29 |
16,9 |
490,1 |
841 |
16,75 |
0 |
1 |
|
н |
28 |
32 |
21,4 |
684,8 |
1024 |
16,9 |
1 |
1 |
с |
|
29 |
20 |
16,8 |
336 |
400 |
16,3 |
0 |
1 |
|
н |
30 |
31 |
16,7 |
517,7 |
961 |
16,85 |
1 |
0 |
|
н |
31 |
29 |
19,6 |
568,4 |
841 |
16,75 |
0 |
1 |
|
н |
32 |
28 |
15,1 |
422,8 |
784 |
16,7 |
0 |
0 |
с |
|
33 |
33 |
16,2 |
534,6 |
1089 |
16,95 |
1 |
0 |
|
н |
34 |
23 |
16,8 |
386,4 |
529 |
16,45 |
0 |
1 |
|
н |
35 |
27 |
18,4 |
496,8 |
729 |
16,65 |
0 |
1 |
|
н |
36 |
34 |
16,2 |
550,8 |
1156 |
17 |
1 |
0 |
|
н |
37 |
24 |
16,7 |
400,8 |
576 |
16,5 |
0 |
0 |
с |
|
38 |
28 |
18,3 |
512,4 |
784 |
16,7 |
0 |
1 |
|
н |
39 |
35 |
19,6 |
686 |
1225 |
17,05 |
1 |
1 |
с |
|
40 |
22 |
18,1 |
398,2 |
484 |
16,4 |
0 |
1 |
|
н |
∑ |
1164 |
670,5 |
19583,9 |
35300 |
670,2 |
|
|
19 |
21 |
cреднее |
29,1 |
16,8 |
|
|
|
|
|
|
|
ЗАДАЧА 2.
Из данных о численности населения поселка, приведенных ниже:
год |
1996 |
1997 |
1999 |
2002 |
2004 |
2005 |
2008 |
кол-во, чел |
870 |
865 |
875 |
838 |
845 |
852 |
867 |
1. Вычислить абсолютные и относительные (базисные и цепные) статистические показатели изменения уровней динамики данного ряда.
2. Рассчитать средние показатели динамики ряда.
3. Описать тенденцию с помощью следующих методов сглаживания: а) механического выравнивания по трехлетней и пятилетней скользящим средним; б) аналитического выравнивания по уравнению линейного тренда.
Решение задачи №2.
1. Вычислить абсолютные и относительные (базисные и цепные) статистические показатели изменения уровней динамики данного ряда.
Решение:
Необходимые расчеты произведем в таблице 5.
Абсолютные показатели- является абсолютный прирост.(Δy)
![]()
![]()
Относительные показатели – коэффициент роста (Кр).
Коэффициент роста выраженный в процентах называется темпом роста.(Тр)
![]()
![]()
Темп прироста (Тпр)
Тпр баз=Тр баз-100 Тпр цеп=Тр цеп-100
Абсолютное значение одного процента прироста (ǀ%ǀ) – только цепной.
ǀ%ǀ=0,01*Yi-1
Таблица 5
год |
Y0 |
∆y |
Тр |
Тпр |
│%│ |
|||
б |
ц |
б |
ц |
б |
ц |
|||
1996 |
870 |
▬ |
▬ |
▬ |
▬ |
▬ |
▬ |
▬ |
1997 |
865 |
-5 |
-5 |
99,4 |
99,4 |
-0,6 |
-0,6 |
8,7 |
1999 |
875 |
5 |
10 |
100,6 |
101,2 |
0,6 |
1,2 |
8,65 |
2002 |
838 |
-32 |
-37 |
96,3 |
95,8 |
-3,7 |
-4,2 |
8,75 |
2004 |
845 |
-25 |
7 |
97,1 |
100,8 |
-2,9 |
0,8 |
8,38 |
2005 |
852 |
-18 |
7 |
97,9 |
100,8 |
-2,1 |
0,8 |
8,45 |
2008 |
867 |
-3 |
15 |
99,7 |
101,8 |
-0,3 |
1,8 |
8,52 |
2. Рассчитать средние показатели динамики ряда.
Решение:
Данный ряд динамики является моментным - характеризует состояние явления на данный момент времени и не равноотстоящий, т.к. расстояния между уровнями ряда не одинаковы.
К средним показателям рядов динамики относятся:
- средний уровень ряда ()
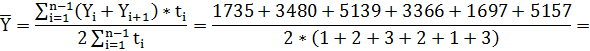
![]()
- средний абсолютный
прирост (![]() )
)
![]()
-средний темп роста
(![]() )
)
![]() %
%
-средний темп прироста ()
![]() =
=![]()
3. Описать тенденцию с помощью следующих методов сглаживания: а) механического выравнивания по трехлетней и пятилетней скользящим средним; б) аналитического выравнивания по уравнению линейного тренда.
Решение:
а) Опишем тенденцию с помощью механического выравнивания по трехлетней и пятилетней скользящим средним.
Необходимые расчеты произведем в таблице 6.
Таблица 6
год |
1996 |
1997 |
1999 |
2002 |
2004 |
2005 |
2008 |
кол-во, чел |
870 |
865 |
875 |
838 |
845 |
852 |
867 |
3-летняя скользящая сумма |
▬ |
2610 |
2578 |
2558 |
2535 |
2564 |
▬ |
3-летняя скользящая средняя |
▬▬ |
870 |
859 |
853 |
845 |
855 |
▬ |
5-летняя скользящая сумма |
▬ |
▬ |
4293 |
4275 |
4277 |
▬ |
▬ |
5-летняя скользящая средняя |
▬ |
▬ |
859 |
855 |
855 |
▬ |
▬ |
Тенденцию механического выравнивания по трехлетней и пятилетней скользящим средним представим графически.
б) Опишем тенденцию с помощью аналитического выравнивания по уравнению линейного тренда.
Необходимые расчеты произведем в таблице 7.
Для аналитического сглаживания с помощью уравнения линейного тренда используем систему уравнений для регрессивного анализа.
Yt=a+bt
a=868,5
b=-2,4
Таблица 7
год |
t |
y |
ty |
t^2 |
Yt |
1996 |
1 |
870 |
870 |
1 |
866,1 |
1997 |
2 |
865 |
1730 |
4 |
863,7 |
1999 |
3 |
875 |
2625 |
9 |
861,3 |
2002 |
4 |
838 |
3352 |
16 |
858,9 |
2004 |
5 |
845 |
4225 |
25 |
856,5 |
2005 |
6 |
852 |
5112 |
36 |
854,1 |
2008 |
7 |
867 |
6069 |
49 |
851,7 |
Сумма: |
28 |
6012 |
23983 |
140 |
6012,3 |
![]() %
%
