Практическая часть. Вариант 2. Статистические методы анализа численности состава населения.

ЗАДАЧА 1.

На основании данных обследования жителей поселка (табл. 1):

1. Провести группировку жителей по доходу с равными интервалами и оптимальным числом групп и представить полученные данные в виде статистического ряда распределения. На основе полученного ряда построить гистограмму, полигон и кумуляту распределения жителей по доходу.

2.Составить и назвать статистическую таблицу с групповым подлежащим, содержащим 5 групп с произвольными интервалами и простым сказуемым, построенным по количественному признаку, содержащим 4 группы с равными интервалами.

3. Сгруппировать жителей поселка: а) по полу; б) по уровню образования. Определить относительные показатели половой и образовательной структур жителей, размер среднего дохода и средний возраст для каждого пола и каждого вида образования.

4. Исчислить по сгруппированным выше данным половой структуры (пункт 3а) средний возраст жителей с помощью следующих средних (простых и взвешенных): а) арифметической; б) гармонической; в) геометрической.

5. Рассчитать показатели вариации дохода жителей поселка: а) по сгруппированным выше данным образовательной структуры (пункт 3б) с использованием средней арифметической простой и взвешенной; б) по несгруппированным данным.

6. Определить модальные и медианные значения дохода жителей: а) по несгруппированным данным; б) из статистического ряда распределения (пункт 1) аналитически и графически.

7. Приняв данные таблицы 1 как результат 5%-ного выборочного обследования жителей поселка, определить среднюю ошибку выборки для среднего дохода жителей. Указать с вероятностью 0,954 пределы возможных значений этих показателей в генеральной совокупности для повторного и бесповторного отбора.

8. Вычислить параметры линейного уравнения регрессии для зависимости дохода жителей от их возраста. Определить тесноту связи между признаками с помощью коэффициента корреляции знаков (коэффициента Фехнера).

Таблица 1

Данные обследования населения поселка в возрасте 20-40 лет

(в графах «Обр.» (образование): в - высшее, с-с – среднее специальное, с – среднее; «Возр.» - возраст; «Дох.» - средний месячный доход за год, тыс. руб.)

№	Пол	Обр.	Возр.	Дох.	№	Пол	Обр.	Возр.	Дох.
1	м	с-с	37	13,8	21	ж	с-с	22	16,6
2	ж	с-с	39	19,6	22	ж	с	38	15,4
3	ж	с-с	21	13,4	23	м	с-с	30	15,9
4	м	с-с	20	17,7	24	ж	в	24	16,2
5	ж	в	25	14,2	25	м	с	33	18,9
6	м	с	29	13,7	26	ж	с-с	22	13,6
7	ж	с-с	36	14,9	27	м	с-с	29	16,9
8	ж	в	28	19,6	28	ж	в	32	21,4
9	м	с	24	16,2	29	ж	с-с	20	16,8
10	ж	в	26	16,5	30	ж	с-с	31	16,7
11	м	с-с	38	17,4	31	м	с	29	19,6
12	ж	с-с	33	17,6	32	ж	с-с	28	15,1
13	ж	в	40	16,4	33	м	в	33	16,2
14	м	с-с	40	16	34	ж	с-с	23	16,8
15	ж	в	23	15,8	35	м	с	27	18,4
16	м	с-с	21	15,9	36	ж	с-с	34	16,2
17	м	с	27	17,8	37	м	с	24	16,7
18	ж	с-с	25	15,9	38	ж	в	28	18,3
19	м	в	33	17,3	39	м	с-с	35	19,6
20	ж	с-с	35	17,4	40	ж	с-с	22	18,1

Решение задачи №1.

1. Провести группировку жителей по доходу с равными интервалами и оптимальным числом групп и представить полученные данные в виде статистического ряда распределения. На основе полученного ряда построить гистограмму, полигон и кумуляту распределения жителей по доходу.

Решение:

Определим оптимальное количество групп. (n)

n=1+3,3lg40=1+3,3*1,602 6

Определим шаг. (h)

h

Построим статистический ряд распределения с учетом вычисленных данных:

№	Доход, тыс. руб.	Кол-во жителей
		Абсолютное	Относительное,%
1	13,4-14,7	5	12,5
2	14,7-16,0	8	20
3	16,1-17,4	15	37,5
4	17,5-18,8	6	15
5	18,8-20,1	5	12,5
6	20,1-21,4	1	2,5
Итого:		40	100

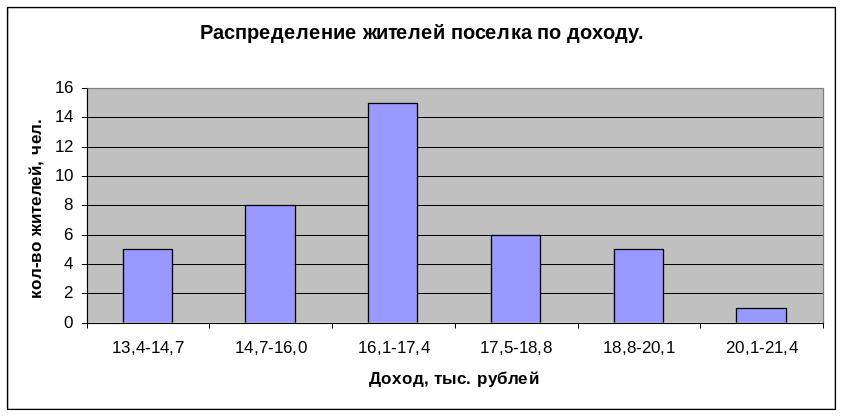
На основе полученного ряда построим гистограмму, полигон и кумуляту распределения жителей по доходу.

Гистограмма+полигон.